算法典型例题：N皇后问题，五种解法，逐步优化（非递归版）
本文将介绍N皇后问题的五种解法，包括朴素回溯法、对称优化、标记优化、可用优化、位运算优化，对于每种解题思路，提供相应的非递归版代码实现。
本文将介绍N皇后问题的五种解法，包括朴素回溯法、对称优化、标记优化、可用优化、位运算优化，对于每种解题思路，提供相应的非递归版代码实现，最后将对每种解法进行测试，横向对比每种解法的求解时间。
题目描述
在 \(N×N\) 格的国际象棋上摆放 \(N\) 个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法？
回溯法
解题思路
回溯法采用深度有限的搜索策略遍历问题的解空间树，可采用递归方式实现，也可采用非递归方式实现，由于递归方式理解起来较为简单，故本文各方法均不提供递归方式，只提供非递归方式。
代码实现
/**
* N皇后问题：回溯法（所有下标均从1开始）
* @param n 皇后的数量
* @return 摆法的数量
*/
int queen(int n) {
// 棋盘 当前放置哪个皇后 解的数量
int q[n + 1], k = 1, res = 0;
memset(q, 0, sizeof q);
// 判断第k个皇后放置位置是否合适
auto check = [&](int k) {
for (int i = 1; i < k; ++i)
// 同列、同斜线已存在皇后
if (q[i] == q[k] || abs(q[i] - q[k]) == abs(i - k))return false;
return true;
};
// 开始放置皇后
while (k > 0) {
// 第k个皇后尝试下一个位置
q[k]++;
// 寻找第k行的下一个可以放置的位置
while (q[k] <= n && !check(k))q[k]++;
// 已超过当前行的上限l，回溯，返回上一行
if (q[k] > n)--k;
// 如果放置完所有皇后，则记录结果，否则放置下一行
else k == n ? res++ : q[++k] = 0;
}
return res;
}
时间复杂度：\(O(n^{n^n})\)。
空间复杂度：\(O(n)\)。
对称优化
解题思路
仔细观察N-皇后的解，发现一种方案可以通过“对称”得到另一种方案。以“左右对称”为例，当 \(N=5\)，限定第一行皇后在左边一半区域时，方案数为 \(6\)，如图 \(1\) 所示。
（N皇后的可行解存在七种对称关系，此处仅讨论左右对称。）
图1
通过“左右对称”可以获得另一方案，同时发现，后面有两种方案重复，去除重复方案后，剩下的刚好是 \(N=5\) 时的全部方案，如图 \(2\) 所示。
图2
当 \(N\) 为偶数时关于中间那条线对称，当 \(N\) 为奇数时关于中间那一列对称。利用左右对称可以使得工作量减少一半，为此，在放置皇后时，增加两条限制
- 第一行的皇后只放在左边一半区域，也即位置小于等于 \((n+1)/2\)；
- 当 \(N\) 为奇数且第一行皇后刚好放在 \((n+1)/2\) 位置（即中间）时，为避免重复，第二行皇后必须放在左边一半区域。
代码实现
/**
* N皇后问题：对称优化（所有下标均从1开始）
* @param n 皇后的数量
* @return 摆法的数量
*/
int queen(int n) {
// 特判
if (n == 1)return 1;
// 棋盘 当前放置哪个皇后 解的数量
int q[n + 1], k = 1, res = 0;
memset(q, 0, sizeof q);
// 判断第k个皇后放置位置是否合适
auto check = [&](int k) {
for (int i = 1; i < k; ++i)
// 同列、同斜线已存在皇后
if (q[i] == q[k] || abs(q[i] - q[k]) == abs(i - k))return false;
return true;
};
// 中点位置 当前行最多能放到第几列
int m = (n + 1) >> 1, l;
// n是否为奇数
bool odd = n & 1;
// 开始放置皇后
while (k > 0) {
// 第k个皇后尝试下一个位置
q[k]++;
// 第一行放置的皇后不能超过中点
if (k == 1)l = m;
// n为奇数且第一行放在中间时，第二行不能超过中间
else if (k == 2 && odd && q[1] == m)l = m - 1;
// 其它情况可以放到中点右边
else l = n;
// 寻找第k行的下一个可以放置的位置
while (q[k] <= l && !check(k))q[k]++;
// 已超过当前行的上限l，回溯，返回上一行
if (q[k] > l)--k;
// 如果放置完所有皇后，则记录结果，否则放置下一行
else k == n ? res++ : q[++k] = 0;
}
return res << 1;
}
时间复杂度：\(O(n^{n^n})\)。
空间复杂度：\(O(n)\)。
标记优化
解题思路
对于棋盘单元坐标，有如下规律（图 \(2\) 为两个 \(4×4\) 的棋盘）：
- 同一正斜线所占据的单元的横纵坐标之和相等。
- 同一反斜线所占据的单元的横纵坐标之差相等。
图3
由此，可以设置数组 \(L\) 和 \(R\)，表示斜线的占有情况，从而可以做到快速判断某位置是否可以放置皇后。
① \(L[i]\) 表示和为 \(i\) 的正斜线是否被占据，\(i\) 的范围为 \([2,2N]\)，故 \(0,1\)两个位置舍去不用。
② \(R[i]\) 表示差为 \(i\) 的反斜线是否被占据，\(i\) 的范围为 \([1-N,N-1]\)，为避免负下标，对 \(i\) 作加 \(N\) 处理。
\(L[i]\) 中的 \(i\) 舍去 \(0,1\) 两个位置，\(R[i]\) 中的 \(i\) 加 \(N\) 而不是加 \(N-1\)，都是为了减少计算量。
同时，再设置数组 \(Y\)，\(Y[i]\) 表示第 \(i\) 列是否被占据，\(1≤i≤N\)。改用根据数组 \(L,R,Y\) 来判断某位置是否可以放置皇后，可减少大量判断。（ \(Y[i]\) 中的 \(i\) 不从 \(0\) 开始是为了便于处理）。
此处统一约定，对于标志数组 \(L,R,Y\)，值为 \(1\) 表示占用，值为 \(0\) 表示未占用。以 \(L\) 为例，\(L[i]=1\) 表示正斜线 \(i\) 被占用。
代码实现
/**
* N皇后问题：标记优化（所有下标均从1开始）
* @param n 皇后的数量
* @return 摆法的数量
*/
int queen_3(int n) {
// 特判
if (n == 1)return 1;
// 棋盘 当前放置哪个皇后 解的数量
int q[n + 1], k = 1, res = 0;
memset(q, 0, sizeof q);
// 标志数组
int y[n + 1], l[2 * n + 1], r[2 * n];
memset(y, 0, sizeof(y)), memset(l, 0, sizeof(l)), memset(r, 0, sizeof(r));
// 中点位置、当前行最多能放到第几列
int w = (n + 1) >> 1, e;
// N是否为奇数
bool odd = n & 1;
// 开始求解
while (k > 0) {
// 当前行放置下一个位置前，把原来占有的位置释放
if (q[k] != 0)
y[q[k]] = l[k + q[k]] = r[k - q[k] + n] = 0;
// 第k个皇后尝试下一个位置
q[k]++;
// 第一行放置的皇后不能超过中点
if (k == 1)e = w;
// n为奇数且第一行放在中间时，第二行不能超过中间
else if (k == 2 && odd && q[1] == w)e = w - 1;
// 其它情况可以放到中点右边
else e = n;
// 寻找第k行的下一个可以放置的位置
while (q[k] <= e && (y[q[k]] || l[k + q[k]] || r[k - q[k] + n]))q[k]++;
// 已超过当前行的上限E，回溯，返回上一行
if (q[k] > e)--k;
// 找到一个解
else if (k == n) res++;
else {
// 标记所在的列、斜线为不可放置
y[q[k]] = l[k + q[k]] = r[k - q[k] + n] = 1;
// 放置下一行
q[++k] = 0;
}
}
return res << 1;
}
时间复杂度：\(O(n^n)\)。
空间复杂度：\(O(n)\)。
可用优化
解题思路
前面两种实现，总是从当前行的第一个位置开始尝试，即使当前行没有位置可以放置，也需尝试完当前行每一个位置，这显然是没有必要的。新增 \(next\) 数组，\(next[i]\) 表示位置 \(i\) 的下一个可用位置（可用列），\(next[0]\) 表示第一个可用位置，\(next[i]=0\) 表示 \(i\) 是最后一个可用位置，特别的，\(next[0]=0\) 表示无可用位置，此时需要回溯。既然已经知道哪些位置可用，那就不再需要数组 \(Y\) 来判断某列是否可用。
代码实现
/**
* N皇后问题：可用优化（所有下标均从1开始）
* @param n 皇后的数量
* @return 摆法的数量
*/
int queen(int n) {
// 特判
if (n == 1)return 1;
// 棋盘 当前放置哪个皇后 解的数量
int q[n + 1], k = 1, res = 0;
memset(q, 0, sizeof q);
// 中点位置 当前行最多能放到第几列
int w = (n + 1) >> 1, e;
// n是否为奇数
bool odd = n & 1;
// 标志数组
int nex[n + 1], l[2 * n + 1], r[2 * n];
memset(l, 0, sizeof(l)), memset(r, 0, sizeof(r));
// 建立可用列链表
for (int i = nex[n] = 0; i < n; ++i) nex[i] = i + 1;
// 当前节点 cur前驱 临时节点
int cur, pre, t;
// 开始求解
while (k > 0) {
// cur指向第一个可用位置
pre = 0, cur = nex[pre];
// 第一行放置的皇后不能超过中间
if (k == 1)e = w;
// N为奇数且第一行放在中间时，第二行不能超过中间
else if (k == 2 && odd && q[1] == w)e = w - 1;
// 其它情况超过中间
else e = n;
/**
* 寻找第k行的下一个可以放置的位置
* !l[k+cur]&&!r[k-cur+n]&&q[k]<=cur：cur需要满足的条件，q[k]<=cur保证当前行尝试的位置会“一直前进”
* cur=0: 链表为空或者找到最后未发现满足条件的列
* cur>e：cur已超过当前行设定的边界，即基础实现中添加的两个限制条件
* cur&&cur<=E用以限定cur的边界
*/
while (cur && cur <= e && (l[k + cur] || r[k - cur + n] || q[k] > cur))
pre = cur, cur = nex[pre];
// 放置当前行时，把当前行原先占有的位置释放
if (q[k]) {
// 恢复成放置原先位置前的状态
t = nex[q[k]];
nex[q[k]] = nex[t];
nex[t] = q[k];
// 保持pre为cur的前驱
if (nex[q[k]] == cur)pre = q[k];
// 标记所在斜线可放置
l[k + q[k]] = r[k - q[k] + n] = 0;
}
// 未找到合适的列，回溯
if (!cur || cur > e)k--;
// 找到合适的列但当前行是最后一行，放完再回溯
else if (k == n) {
q[k] = cur;
res++, k--;
}
// 找到合适的列但非最后一行，放完后放置下一行
else {
q[k] = cur;
nex[pre] = nex[cur]; // cur已被占用，删除cur
nex[cur] = pre; // 记录前驱，用以恢复到放置前的状态
l[k + cur] = r[k - cur + n] = 1; // 标记所在斜线不可放置
q[++k] = 0; // 放置下一行
}
}
return res << 1;
}
时间复杂度：\(O(n!)\)。
空间复杂度：\(O(n)\)。
位运算
解题思路
以 \(3×3\) 的棋盘为例，最左上角的左斜线记作第一条左斜线，最右上角的第一条右斜线记作第一条右斜线。为了便于叙述，以下涉及到的二进制均只有 \(n\) 位（棋盘大小），第几位是从左往右数。
将列、左斜线（/）、右斜线（\）的可用状态分别用二进制表示，\(1\) 表示占用，\(0\) 表示可用，以列为例，\(010\) 表示第 \(1,3\) 列可用，第 \(2\) 列占用。
将斜线状态转换为列状态，以左斜线为例，如下表所示
| 第1行 | 第2行 | 第3行 | |
|---|---|---|---|
| 第1条左斜线 | 100 | 000 | 000 |
| 第2条左斜线 | 010 | 100 | 000 |
| 第3条左斜线 | 001 | 010 | 100 |
| 第4条左斜线 | 000 | 001 | 010 |
| 第5条左斜线 | 000 | 000 | 001 |
（第 \(1\) 条左斜线，第 \(1\) 行）= \(100\) 的解释为，若第 \(1\) 条左斜线不可用，对于第 \(1\) 行的影响是 \(100\)，即，第 \(1\) 列不能放置，第 \(2,3\) 列可以放置。
对于第 \(i\) 行而言，必须要放置一个皇后（放置不了就直接回溯了），放置完皇后，其对应左斜线状态必然不是 \(000\)，因为放置的这个皇后必然会导致某左斜线不可用，所以，假设第 \(i\) 行到第 \(i+1\) 行，左斜线状态状态由 \(A➡B\)，则 \(A\) 必定不为 \(000\)，在上表所有状态转换（由第 \(j\) 行到第 \(j+1\)）中，排除起始状态为 \(000\) 的转换，\((i,j+1)\) 可由 \((i,j)\) 左移一位得到。
同理可得，对于右斜线而言，\((i,j+1)\) 可由 \((i,j)\) 右移一位得到。
设考虑第 \(i\) 行时，列、左斜线、右斜线状态分别为 \(C,L,R\)，则
- 第 \(i\) 行可选的位置为 \(pos = ~(C | L | R) \& ((1<<n)-1)\) 的二进制中 \(1\) 对应的列，假设选的是第 \(k\) 列，则记为 \(P\)，\(P\) 的二进制中只有第 \(k\) 位为 \(1\)。
- 考虑第 \(i\) 行时，\(C = C|P\)，\(L = (L|P)<<1\)，\(R = (R|P)>>1\)。
注意，\(C,L,R\) 需要始终保持只有 \(n\) 位有效，由于整数 \(int\) 有 \(32\) 位，那么除开低 \(n\) 位，其余各位均需保持为 \(0\)。
代码实现
/**
* N皇后问题：位运算
* @param n 皇后的数量
* @return 摆法的数量
*/
int queen((int n) {
int res = 0, mk = (1 << n) - 1, k = 1, pos, p;
// 存放放置各行时的状态
tuple<int, int, int, int> st[n + 2];
// 第一行
st[1] = {0, 0, 0, 0};
while (k > 0) {
/**
* c表示列状态
* l表示左斜线状态
* r表示右斜线状态
* m指示当前行哪些列已经尝试过了
*/
auto [c, l, r, m] = st[k];
// 当前行可放置的位置
pos = ~(c | l | r | m) & mk;
// 无可放置的位置则回溯
if (!pos) {
k--;
continue;
}
// 取pos最低位的1
p = pos & (-pos);
// 记录当前行的位置p已尝试过
st[k] = {c, l, r, m | p};
// 状态传递，初始放置下一行时的状态，尝试放置下一行
if (k < n) st[++k] = {c | p, (l | p) << 1, (r | p) >> 1, 0};
// 放置完毕则记录答案并回溯
else res++, k--;
}
return res;
}
时间复杂度：\(O(n!)\)。
空间复杂度：\(O(n)\)。
统计与分析
五种解法均采用非递归实现，为了直观比较五种解法的效率，分别统计五种解法在 \(N=10\) 到 \(N=18\) 的情况下的求解时间（单位为毫秒），测试结果如下表所示。
| 解法\N | 10 | 11 | 12 | 13 | 14 | 15 | 116 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|
| 回溯法 | 5 | 24 | 137 | 791 | 5193 | 35500 | 256075 | 2005077 | 16683871 |
| 对称优化 | 3 | 13 | 75 | 469 | 3037 | 20814 | 152299 | 1164780 | 9376002 |
| 标记优化 | 0 | 4 | 24 | 135 | 809 | 5206 | 35373 | 253702 | 1912227 |
| 可用优化 | 1 | 3 | 16 | 89 | 526 | 3334 | 22420 | 158374 | 1179343 |
| 位运算 | 5 | 25 | 128 | 703 | 4144 | 25866 | 177143 | 1263102 | 9281287 |
根据上表数据制作散点图，如图 \(4\) 所示：
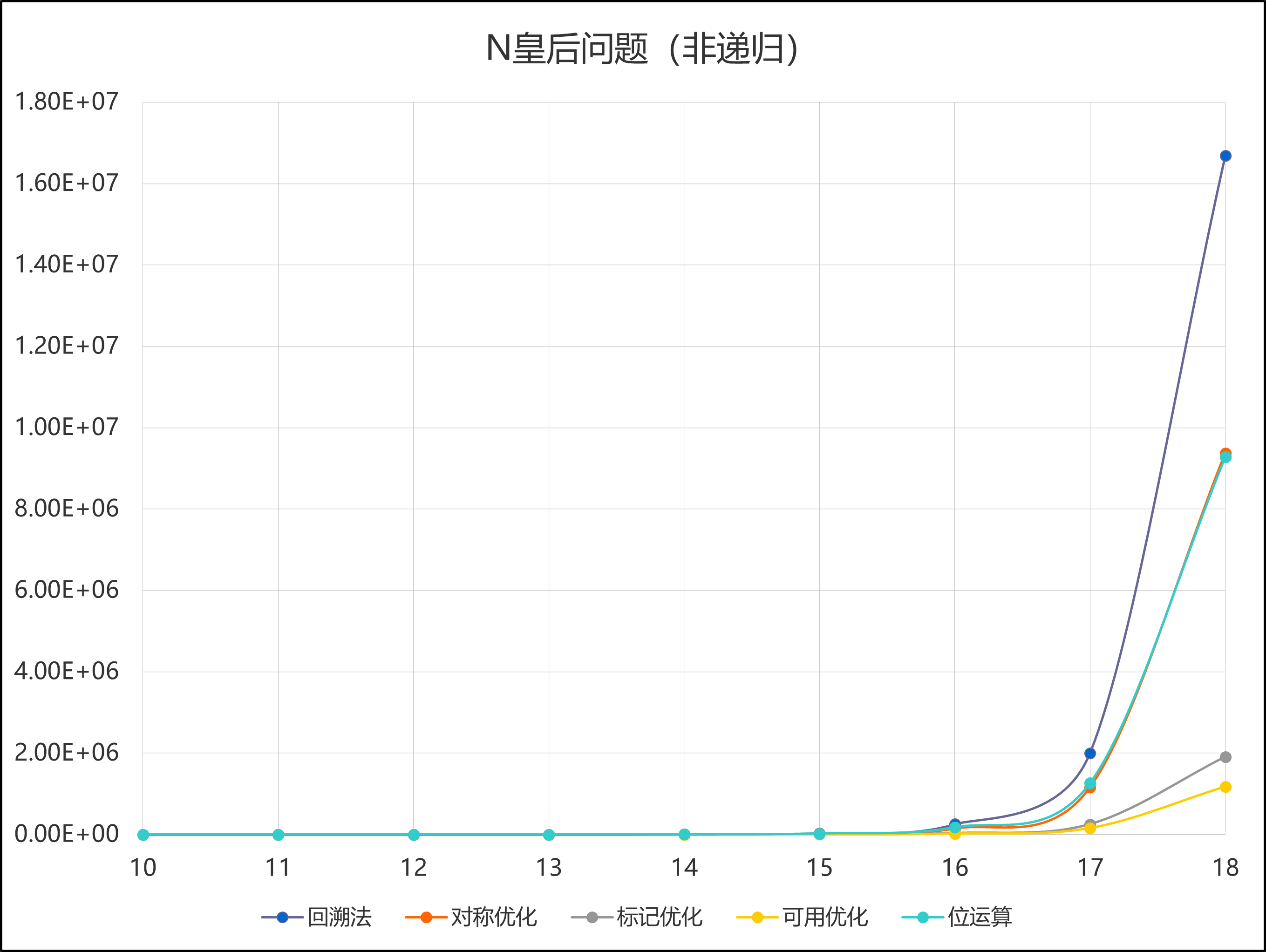
图4 N皇后问题非递归求解时间散点图
从回溯法到可用优化，通过逐步优化求解方式，求解时间也显著减少。位运算方式与对称优化方式的求解时间相当，\(N <18\) 时，位运算的求解时间大于对称优化，但是，由数据可以预见，当 \(N≥18\) 时，位运算的求解时间将小于对称优化。
END
文章文档：公众号 字节幺零二四 回复关键字可获取本文文档。
浙公网安备 33010602011771号