【笔记】机器学习基础 - Ch5. Support Vector Machines

5.1 Linear classification

考虑如下问题：$\mathbb{R} ^N$ 上的 $\cal X$ 服从某个未知分布 $\cal D$，并由目标函数 $f:\cal X\to Y$ 映射到 $\{-1, +1\}$。根据采样 $S=(({\bf x} _1, y _1),\dotsb, ({\bf x} _m, y _m))$ 确定一个二分类器 $h\in \cal H$，使得其泛化误差 $R _{\cal D}(h)=\Pr _{{\bf x}\sim \cal D}[h({\bf x})\ne f({\bf x})]$ 尽量小
选择线性分类器 linear classifier 使得复杂度比较小，即：

$${\cal H}=\{{\bf x}\mapsto \text{sign}({\bf w\cdot x}+b):{\bf w}\in \mathbb{R} ^N-\{{\bf 0}\}, b\in \mathbb{R}\}$$

也就是通过超平面 hyperplane 二分类。另外 ${\bf w\cdot x}+b$ 和 ${\bf -w\cdot x}-b$ 代表同一个超平面但是标签取反，可以把 $\bf 0$ 代入判断一下正例位置。

5.2 Separable case

本节假设样本 $S$ 线性可分，也就是样本的标签是某个待学习的超平面 $({\bf w},b)$ 对样本进行映射得到的：$\forall i\in[m],y _i({\bf w \cdot x _{\it i}}+b)\ge 0$
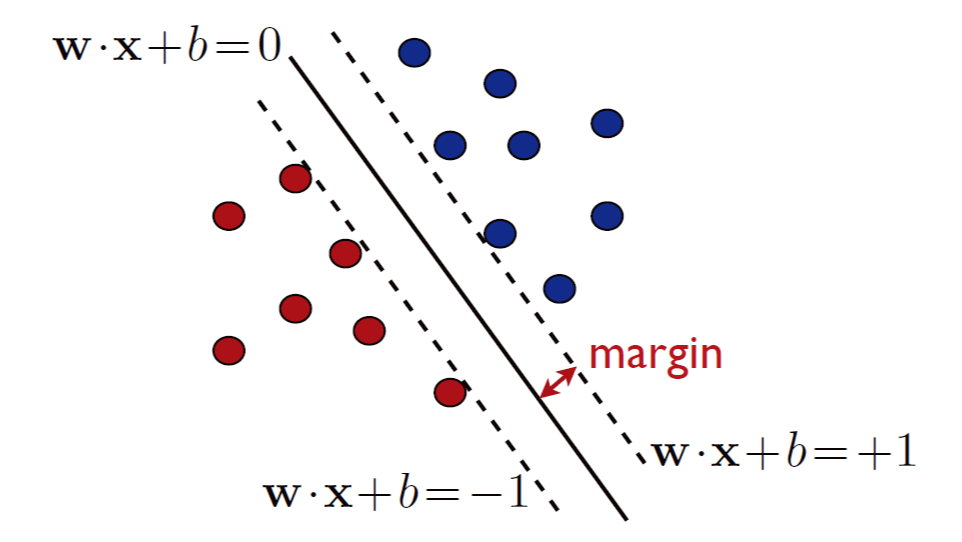
SVM 考虑几何间隔 geometric margin

定义 Geometric margin
点 $\bf x$ 和超平面 $h:({\bf w},b)$ 的几何间隔，定义为两者的欧几里得距离 $\rho _h({\bf x})$：

$$\rho _h({\bf x})=\frac{|{\bf w\cdot x}+b|}{\Vert {\bf w}\Vert _2}$$

小证一下：设沿 $\bf x$ 方向与平面交于 $\bf x'$，那么距离就是 $\bf x-x'$ 在 $\bf w$ 方向的投影长度，即 $\rho={\bf |(x-x')\cdot\frac{w}{\Vert w\Vert}|}=\frac{\bf |w\cdot x-w\cdot x'|}{\bf \Vert w\Vert}=\frac{|({\bf w\cdot x}+b)-({\bf w\cdot x'}+b)|}{\bf \Vert w\Vert}=\frac{|{\bf w\cdot x}+b|}{\bf \Vert w\Vert}$
定义线性分类器对样本 $S$ 的几何距离为 $\rho _h=\min\rho _h({\bf x} _i)$，而 SVM 应取到最大的几何距离，有：

$$\begin{aligned} {\bf w},b &= \underset{{{\bf w},b\ :\ y _i({\bf w\cdot x} _i+b)\ge 0}}{\text{arg max}}\min _i \frac{|{\bf w\cdot x} _i+b|}{\Vert {\bf w}\Vert} \\ &= \underset{{\bf w},b}{\text{arg max}}\ \min _i \frac{y _i({\bf w\cdot x} _i+b)}{\Vert {\bf w}\Vert} \qquad;\text{假设样本线性可分} \\ &= \underset{{\bf w},b\ :\ \min y _i({\bf w\cdot x} _i+b)=1}{\text{arg max}} \ \frac{1}{\Vert {\bf w}\Vert} \qquad;\text{加条件约束分式上下变动} \\ &= \underset{{\bf w},b\ :\ y _i({\bf w\cdot x} _i+b)\ge 1}{\text{arg max}} \ \frac{1}{\Vert {\bf w}\Vert} = \underset{{\bf w},b\ :\ y _i({\bf w\cdot x} _i+b)\ge 1}{\text{arg min}} \ \frac{1}{2}{\Vert \bf w\Vert} ^2 \qquad;\text{凸化} \end{aligned}$$

从而得到如下对 $({\bf w}, b)$ 的凸优化问题：

$$\min _{{\bf w}, b} \frac{1}{2}\Vert {\bf w} \Vert ^2 \\ subject\ to: g _i({\bf w},b)=1 - y _i({\bf w\cdot x} _i + b)\le 0,\forall i\in [m]$$

根据以二阶导定义的凸函数，由于 $F:{\bf w\to \Vert w\Vert} ^2/2$ 的 Hessian $\nabla ^2 F=\bf I$ 是正定的，故 $F$ 是严格的凸函数；而约束 $g _i$ 均为仿射函数，故该优化问题有唯一解。
（这类目标函数为平方次、约束为仿射的问题，属于二次规划问题 quadratic programming (QP)，已有大量相关算法；对于 SVM 问题有 block coordinate descent 等算法）
由于约束都是仿射，该问题与对偶问题等价，因此转到对偶问题：

引入 Lagrange 变量 ${\boldsymbol{\alpha}}=(\alpha _1, \dotsb, \alpha _m)'\ge 0$，定义 Lagrangian ${\cal L}({\bf w}, b, {\boldsymbol{\alpha}})$ 并给出最优解的 KKT 条件：

$${\cal L}({\bf w}, b, {\boldsymbol{\alpha}}) = \frac{1}{2}\Vert {\bf w} \Vert ^2 + \sum _{i=1} ^m \alpha _i [1- y _i({\bf w\cdot x} _i + b)]\\ \begin{aligned} & \nabla _{\bf w}{\cal L}={\bf w}-\sum _{i=1} ^{m}\alpha _i y _i {\bf x} _i = 0 &&\implies {\bf w}=\sum _{i=1} ^{m}\alpha _i y _i {\bf x} _i \\ & \nabla _{b}{\cal L}=-\sum _{i=1} ^{m}\alpha _i y _i = 0 &&\implies \sum _{i=1} ^{m}\alpha _i y _i = 0 \\ & {\boldsymbol{\alpha}}\cdot {\bf g}({\bf w},b)=0 &&\implies \forall i\in [m],\alpha _i =0\vee y _i({\bf w\cdot x} _i + b)=1 \end{aligned} ;\text{KKT}$$

根据条件，$\bf w$ 为若干 $\alpha _i$ 不为零的样本 ${\bf x} _i$（称为支持向量 support vector）的线性组合，且这些向量必定落在 ${\bf w\cdot x} + b=\pm 1$ 的平面上。注意到即使 $({\bf w},b)$ 有唯一解，$\boldsymbol{\alpha}$ 却不一定唯一，因为只需要 $N+1$ 个向量就能定义一个 $N$ 维平面
利用 KKT 条件消去 ${\bf w}, b$，得到对偶问题：

$$\max _{\boldsymbol{\alpha}} {\cal L}=\max _{\boldsymbol{\alpha}}\left[ \sum _{i=1} ^m \alpha _i - \frac{1}{2}\sum _{i=1} ^m \sum _{j=1} ^m (\alpha _i y _i {\bf x} _i) \cdot (\alpha _j y _j {\bf x} _j)\right] \\ subject\ to: {\boldsymbol{\alpha}}\ge {\bf 0}\wedge \Sigma _{i=1} ^{m}\alpha _i y _i = 0$$

这个问题同样是凸优化问题（$\nabla ^2 _{\boldsymbol{\alpha}}{\cal L}\preceq\bf 0$，concave，且为二次项，是 QP 问题，可用 SMO 算法解决）
解出 ${\boldsymbol{\alpha}}$ 后，就能得到对偶原问题的解：

$${\bf w}=\sum _{i=1} ^{m}\alpha _i y _i {\bf x} _i,\quad b=y _{sv} - {\bf w \cdot x} _{sv}\quad;\text{for any support vector $sv$}$$

从而得到假设平面 $h(\bf x)$

$$h({\bf x})=\text{sgn}({\bf w\cdot x} + b)=\text{sgn}\left(\sum _{i=1} ^m \alpha _i y _i({\bf x} _i\cdot {\bf x}) + b\right)$$

注意到假设平面只用到支持向量与输入向量的内积，我们之后在这一点上可以做文章，例如引入核方法
最后，几何间隔 $\rho ^2=1/{\Vert\bf w \Vert _2 ^2}=1/\sum _{i=1} ^m \alpha _i=1/{\Vert\boldsymbol{\alpha}\Vert _1}$，证明只需上述求 $b$ 的式子两边同乘 $\sum \alpha y$ 即可

Leave-one-out analysis
依然认为样本标签为通过某个超平面映射、始终是线性可分的
我们给泛化误差（的期望）一个上界，分析式子：

$$\begin{aligned} \mathbb{E} _{S\sim \cal D ^m}[R(h _S)] &= \mathbb{E} _{S\sim \cal D ^m}\left[\mathbb{E} _{x\sim \cal D}[1 _{h _S(x)\ne y}]\right] \\ &= \mathbb{E} _{S\sim \cal D ^m, x\sim \cal D}\left[1 _{h _S(x)\ne y}\right] \\ &= \mathbb{E} _{S'\sim \cal D ^{m+1}}\left[1 _{h _{S'/{x _1}}(x _1)\ne y _1}\right]=\mathbb{E} _{S'\sim \cal D ^{m+1}}\left[1 _{h _{S'/{x _2}}(x _2)\ne y _2}\right]=\cdots \\ &= \mathbb{E} _{S'\sim \cal D ^{m+1}}\left[\frac{1}{m+1}\sum _{i=1} ^{m+1} 1 _{h _{S'/\{x _i\}}(x _i)\ne y _i}\right] \end{aligned}$$

期望式内类似对 $m+1$ 个样本使用留一法，因此定义算法 $\cal A$ 对样本 $S'=((x _1,y _1),\dots, (x _{m+1}, y _{m+1}))$ 的 Leave-one-out error $\widehat{R} _\text{LOO}({\cal A})$，为用剩余样本分类留出样本的平均误差，并对其放缩：

$$\widehat{R} _\text{LOO}({\cal A}) = \frac{1}{m+1}\sum _{i=1} ^{m+1} 1 _{h _{S'/\{x _i\}}(x _i)\ne y _i} \le \frac{N _{SV}(S')}{m+1}$$

其中 $N _{SV}(S')$ 是用 SVM 分类 $S'$ 得到的支持向量个数；显然若某个 $x _i$ 贡献了误差，那么它必定是支持向量之一，否则去掉它不会对分类平面造成影响
结合上述式子，得到：

$$\mathbb{E} _{S\sim \cal D ^m}[R(h _S)]\le \mathbb{E} _{S'\sim \cal D ^{m+1}}[\frac{N _{SV}(S')}{m+1}]$$

这就是我们的上界。一般来说支持向量不会太多，所以右式应该不会很大；但是这个式子只对所有情况的平均值给出上界，并不是之前提到 PAC 形式。后面会给出更强的 high-probability bounds。

5.3 Non-separable case

也就是对任意 $({\bf w}, b)$ 总存在 $i\in [m]$ 使得 $y _i({\bf w\cdot x} _i + b)\not \ge 1$，一种常用的松弛做法，是引入松弛变量 slack variables $\xi\ge 0$：

$$y _i[{\bf w\cdot x} _i + b] \ge 1-\xi _i\ ,\quad \forall i\in [m],\xi _i\ge 0$$

考虑到一对矛盾的点：尽可能小的松弛因素 $\sum \xi _i$，或者更一般地 $\sum \xi _i^p$；和尽可能大的几何间隔 $1/\Vert \bf w\Vert$，揉进一个式子，得到关于 ${\bf w}, b, {\boldsymbol{\xi}}$ 的优化问题：

$$\min _{{\bf w}, b, {\boldsymbol{\xi}}} \frac{1}{2}\Vert {\bf w}\Vert ^2 + C\sum _{i=1}^m \xi _i^p \\ subject\ to: y _i({\bf w\cdot x} _i + b)\ge 1-\xi _i \wedge \xi _i \ge 0,i\in [m]$$

其中 $C\ge 0$；一般取 $p=1$，称为 hinge loss
这又是个凸优化问题（仿射约束+待优化函数为凸），扔给 Lagrangian 和 KKT：

$${\cal L}({\bf w}, b, {\boldsymbol{\xi, \alpha,\beta}}) = \frac{1}{2}\Vert {\bf w} \Vert ^2 + C\sum _{i=1}^m \xi _i - \sum _{i=1} ^m \alpha _i [y _i({\bf w\cdot x} _i + b) -1 +\xi _i ] - \sum _{i=1} ^m \beta _i \xi _i \\ \begin{aligned} & \begin{aligned} \nabla _{\bf w}{\cal L}=0\implies & {\bf w}=\sum _{i=1}^m \alpha _i y _i {\bf x} _i \\ \nabla _{b}{\cal L}=0\implies & \sum _{i=1} ^m \alpha _i y _i = 0 \\ \nabla _{\xi _i}{\cal L} = 0\implies & \alpha _i + \beta _i = C \\ \end{aligned} \\ & \forall i\in [m],\quad \alpha _i [y _i({\bf w\cdot x} _i + b) -1 + \xi _i] = 0 \\ & \forall i\in [m],\quad \beta _i \xi _i = 0 \end{aligned};\text{KKT}$$

观察式子，$\bf w$ 为支持向量的线性组合；对于一个支持向量 $\bf x$，由于 $\alpha\ne 0$，则 $[y ({\bf w\cdot x} + b) -1 + \xi] = 0$，两种情况：若 $\xi=0$，则该向量就落在支持面上，和原本的支持向量一样；若 $\xi \ne 0$，则该点在支持面内侧或者越过分类面（称为 outlier），从而 $\beta=0,\alpha=C$，从而以 $Cy\bf x$ 贡献给 $\bf w$
同样地，$\bf w$ 有唯一解，但是支持向量的解可能不唯一
对偶问题：约到剩下 $\boldsymbol{\alpha,\beta}$，发现 $C\sum \xi _i$ 和拉格朗日项里多出来的那部分抵消了，得到和原本一样的式子；但是条件部分还需要满足 $\alpha\le C$：

$$\max _{\boldsymbol{\alpha}}{\cal L}=\max _{\boldsymbol{\alpha}}\left[ \sum _{i=1} ^m \alpha _i - \frac{1}{2}\sum _{i=1} ^m \sum _{j=1} ^m (\alpha _i y _i {\bf x} _i) \cdot (\alpha _j y _j {\bf x} _j)\right] \\ subject\ to: {\bf 0}\le {\boldsymbol{\alpha}}\le {\bf C}\wedge \Sigma _{i=1} ^{m}\alpha _i y _i = 0$$

又是个 QP，解出 $\boldsymbol{\alpha}$ 后同样有：${\bf w}=\sum _{i=1} ^{m}\alpha _i y _i {\bf x} _i, b=y _{sv} - {\bf w \cdot x} _{sv}$
从而得到假设平面 $h({\bf x})=\text{sgn}({\bf w\cdot x} + b)=\text{sgn}\left(\sum _{i=1} ^m \alpha _i y _i({\bf x} _i\cdot {\bf x}) + b\right)$，它依然只依赖向量内积——之后会在此做文章

5.4 Margin theory

为分类函数 $h$ 提出 “置信间隔 confidence margin” 的概念。
考虑 $yh(x)> 0$ 刻画了分类成功的情况，此时用 $|h(x)|$ 描述这次预测的置信度 confidence。当置信度较低时，即使分类正确，也需要接受一定的惩罚。因此引入置信间隔 $\rho>0$ 和对应的损失函数 $\rho$-margin loss：$\Phi _{\rho}(x)=\min (1,\max(0, 1-x/\rho))$，也就是一个 $(-\infty,1)\to (0,1)\to(\rho,0)\to(+\infty,0)$ 的分段函数
同时定义经验边界损失：

Def. Empirical margin loss
假设 $h$ 关于样本 $S=(x _1,\dotsb, x _m)$ 的 empirical margin loss，为 $\rho$-margin loss $\Phi _\rho$ 的平均值：

$$\widehat{R} _{S,\rho}(h)=\frac{1}{m}\sum _{i=1}^m \Phi _{\rho}(y _i h(x _i))$$

之所以用 $\rho$-margin loss 而不是简单在 $\rho$ 处 0-1 突变，是因为这样保证其斜率最多为 $1/\rho$，也称之为 $1/\rho$-Lipschitz，有可用的定理：

Th. Talagrand's lemma
$\Phi _1,\dotsb, \Phi _m:\mathbb{R}\to \mathbb{R}$ 都是 $l$-Lipschitz 函数，$\sigma _1,\dotsb,\sigma _m$ 是 Rademacher 变量；对任意实函数的假设集合 $\cal H$，关于样本 $S=(x _1,\dotsb, x _m)$，都有：

$$\frac{1}{m}\mathbb{E} _{\boldsymbol{\sigma}}\left[ \sup _{h\in\cal H} \sum _{i=1} ^m \sigma _i ({\color{deeppink}{\Phi _i\circ h}})(x _i) \right] \le \frac{\color{deeppink}{l}}{m} \mathbb{E} _{\boldsymbol{\sigma}}\left[ \sup _{h\in\cal H} \sum _{i=1} ^m \sigma _i {\color{deeppink}{h}}(x _i) \right] = l\cdot \widehat{\frak{R}} _S(\cal H)$$

特别地，若 $\Phi _i=\Phi,i\in[m]$，则该式变为 $\widehat{\frak{R}} _S(\Phi\circ\cal H)\le l\cdot\widehat{\frak{R}} _S(\cal H)$

感性理解，左式某个 $\mathbb{E} _{\sigma}$ 取 $\pm 1$ 可视为某两个 $\Phi _{\sigma}\circ h _1,\Phi _{\sigma}\circ h _2$ 的差，由于斜率限制它不会大于 $h_1,h_2$ 差的 $l$ 倍
证明：
先划分为 $\mathbb{E} _{\sigma _1,\dotsb,\sigma _{m-1}}[\mathbb{E} _{\sigma _m}[\sup \sum _{i=1} ^{m-1}+\sigma _m(\Phi _m\circ h)(x _m)]]$，考虑对 $\mathbb{E} _{\sigma _m}$ 单独放缩
首先是一个套路：

如果要将 $\sup _{h}$ 向上放缩，考虑先松弛 $\sup$，表述为：$\forall \epsilon>0,\exist h _0, (1-\epsilon)\sup _h\le h _0$，再对 $h _0$ 放缩到某个 $g$；相关证毕后再说明该式对任意 $\epsilon$ 均成立，从而有 $\sup _h\le g$ 成立

用该表述，由于有 $\sigma _m$，我们分别用 $h _1,h _2$ 上限住 $\sigma _m=\pm 1$ 的情况，然后把 $\mathbb{E} _{\sigma _m}$ 替换为两者求和
接着，对于两者的 $(\Phi _m\circ h _1)(x _m)-(\Phi _m\circ h _2)(x _m)$，考虑上限住它同时摘掉 $\Phi$，就自然地引入了 $\Phi$ 的变化率，也就是 $l$-Lipschitz 概念，得到其 $\le sl(h _1(x _m)-h _2(x _m))$，其中 $s$ 是修正符号
然后是刚才的逆过程：用 $\sup$ 又上限住两者同时统一形式，一正一负的求和又把 $\mathbb{E} _{\sigma _m}$ 请了回来，最后得到 $\mathbb{E} _{\sigma _m}[\sup \sum _{i=1} ^{m-1}+\sigma _m(\Phi _m\circ h)(x _m)]\le \mathbb{E} _{\sigma _m}[\sup \sum _{i=1} ^{m-1}+\sigma _m l h(x _m)]$；对其他 $\sigma$ 同理即可

利用该定理，给出我们关于泛化误差 $R(h)$ 的上界：

Th. Margin bound for binary classification
$\cal H$ 是映射 $h:\cal X\to \mathbb{R}$ 的集合（以其符号进行二分类）。固定置信间隔 $\rho>0$，以至少 $1-\delta$ 的概率，对任意 $h\in \cal H$ 有：

$$\begin{aligned} R(h)&\le \widehat{R} _{S,\rho}(h) + \frac{2}{\rho}{{{\frak{R}} _{m}}}({\cal H})+\sqrt{\frac{\log \frac{1}{\delta}}{2m}} \\ R(h)&\le \widehat{R} _{S,\rho}(h) + \frac{2}{\rho}{{\widehat{\frak{R}} _{S}}}({\cal H})+3\sqrt{\frac{\log \frac{2}{\delta}}{2m}} \end{aligned}$$

其中 $R(h)=\mathbb{E}[1 _{yh(x)\le 0}],\ \widehat{R} _{S,\rho}(h)=\frac{1}{m}\sum _{i=1}^m \Phi _{\rho}(y _i h(x _i))$

证明，以第一个式子为例，第二个式子同理
首先 $R(h)\le \mathbb{E}[\Phi _{\rho}(yh(x))]$
记 $\widetilde{\cal H}=\{z=(x,y)\mapsto yh(x):h\in \cal H\},\ {\cal G}=\Phi _{\rho}\circ\widetilde{\cal H}$，后者元素为 $g:z\to [0,1]$，代入定理（见 3.1）

$$\mathbb{E}[g(z)]\le \frac{1}{m}\sum _{i=1} ^{m}g(z _i) + 2{{{\frak{R}} _{m}}}({\cal G})+\sqrt{\frac{\log \frac{1}{\delta}}{2m}} \\ \begin{aligned} \implies \mathbb{E}[\Phi _{\rho}(yh(x))] & \le \widehat{R} _{S,\rho}(h) + 2{{{\frak{R}} _{m}}}(\Phi _{\rho}\circ\widetilde{\cal H})+\sqrt{\frac{\log \frac{1}{\delta}}{2m}} \\ & \le \widehat{R} _{S,\rho}(h) + \frac{2}{\rho}{{{\frak{R}} _{m}}}(\widetilde{\cal H})+\sqrt{\frac{\log \frac{1}{\delta}}{2m}} \\ \end{aligned}$$

且 ${\frak{R}} _{m}(\widetilde{\cal H})=\mathbb{E} _{S,\sigma}[\sup _{h\in \cal H}\frac{1}{m}\sum _{i=1}^m \sigma _i y _i h(x _i)]$ 可以直接把 $y _i$ 去掉（可见 Rademacher 变量可以做为有无标签的桥梁），也就是 ${\frak{R}} _{m}({\cal H})$，于是得证

观察式子，它包含关于置信区间 $\rho$ 的 trade-off：增大 $\rho$，第二项会减小，但是第一项会被惩罚地更多。进一步思考：

（这是一个我从未注意过的问题）
既然这是个关于 $\rho$ 的 trade-off，那么我们能不能考虑滑动这个 $\rho$ 以达到一个理想的上界呢？
答案是不能。为什么？
当我们滑动 $\rho$ 时，我们求最值的这个过程等价于承认了这个不等式对滑到的任意 $\rho$ 成立，更完整地说，命题变成：“以至少 $1-\delta$ 的概率，对任意 $\rho$ 成立”
而我们原本的定理是：“对一个 $\rho$ 以至少 $1-\delta$ 的概率成立”。显然两者是不等价的：前者事件是后者的交，而概率会小等于后者
因此我们想要滑动 $\rho$ 的话，我们不能在原定理上滑，我们应该先给出一个对一个范围内的 $\rho$（以某个概率）同时成立的定理

Th. Margin bound for $\rho\in (0,r]$
$\cal H$ 是映射 $h:\cal X\to \mathbb{R}$ 的集合（以其符号进行二分类）。固定 $r>0$，以至少 $1-\delta$ 的概率，对任意 $h\in \cal H,\rho\in (0,r]$ 有：

$$\begin{aligned} R(h)&\le \widehat{R} _{S,\rho}(h) + \frac{4}{\rho}{{{\frak{R}} _{m}}}({\cal H})+\sqrt{\frac{\log \log _2 \frac{2r}{\rho}}{m}} +\sqrt{\frac{\log \frac{2}{\delta}}{2m}} \\ R(h)&\le \widehat{R} _{S,\rho}(h) + \frac{4}{\rho}{{\widehat{\frak{R}} _{S}}}({\cal H})+\sqrt{\frac{\log \log _2 \frac{2r}{\rho}}{m}} +3\sqrt{\frac{\log \frac{4}{\delta}}{2m}} \end{aligned}$$

证明思路，以第一个式子为例：
利用原定理的另一个表述：$\Pr[\sup _{h\in\cal H}\{f(\rho,\epsilon)\}>0]\le \exp(-2m\epsilon ^2)$，$f$ 就是把不等式的项全部移到一边
构造事件序列：$(\rho _k) _{k\ge 1}, ({\epsilon} _k) _{k\ge 1}$，套进该式，然后用 union bound 合并事件：

$$\Pr[\sup _{h\in\cal H, k\ge 1}\{f(\rho _k,\epsilon _k) \}>0]\le \sum _{k\ge 1} \exp(-2m\epsilon _k ^2)$$

后者需要进一步放缩成关于 $\epsilon$ 的式子，往级数求和收敛靠，取 $\epsilon _k=\epsilon + u _k$，狠狠放缩：

$$\begin{aligned}= \sum _{k\ge 1} \exp(-2m(\epsilon +u _k) ^2) \le \exp(-2m\epsilon ^2)\sum _{k\ge 1} \exp(-2mu _k ^2)\end{aligned}$$

根据该式构造 $u _k$：取开方，除以 $m$，再套一个 $\log$，即 $u _k = \sqrt{(\log k)/m}$，丢进去，级数求和收敛：

$$=\exp(-2m\epsilon ^2)\sum _{k\ge 1}1/k ^2=\frac{\pi ^2}{6}\exp(-2m\epsilon ^2)\le 2\exp(-2m\epsilon ^2)$$

得到对事件序列 $(\rho _k) _{k\ge 1}$ 成立的引理，接下来把 $\rho\in (0, r]$ 套进去，假设 $\rho$ 的界对应为 $g(\rho)$，即证明 $\Pr[\sup _{h\in \cal H,\rho\in(0,c]}\{ g(\rho)\}>0]\le \Pr[\sup _{h\in\cal H, k\ge 1}\{f(\rho _k) \}>0]$，不妨证明前者包含于后者，即 $\sup _{h\in \cal H,\rho\in(0,c]}\{ g(\rho)\}\le \sup _{h\in\cal H, k\ge 1}\{f(\rho _k) \}$，不妨证明对任意 $\rho \in(0,c]$，总存在 $\rho _k$ 使得 $g(\rho)\le f(\rho _k)$
由于 $f(\rho _k)=R(h)-\widehat{R} _{S,\rho _k}(h) -\frac{2}{\rho _k}{{{\frak{R}} _{m}}}({\cal H})-\epsilon-\sqrt{(\log k)/m}$，为了向下放缩，可以先取 $\rho _k=r/2 ^k$，从而对于任意 $\rho\in (0,r]$，总存在 $\rho\in(\rho _k,\rho _{k-1}],\rho \le 2\rho _k$，这样设计使得我们同时拥有 $\rho _k, \rho$ 的不同方向的不等号，方便我们对每一项选择其一进行放缩，放缩后的式子即为 $g(\rho)$，从而得证

对于有界情况，先对 Rademacher 复杂度提出一个上界：

Th. Bound for Rademacher complexity, bounded weight vectors case
容量为 $m$ 的样本 $S\sube \{{\bf x:\Vert x\Vert}\le r\}$，假设集合 ${\cal H}=\{{\bf x\mapsto w\cdot x:\Vert w\Vert}\le \Lambda\}$，则 $\cal H$ 的 Rademacher complexity 具有上界：

$$\widehat{\frak{R}} _S({\cal H})\le \sqrt{\frac{r ^2 \Lambda ^2}{m}} \\ {\frak{R}} _m({\cal H})=\mathbb{E} _{S}[\widehat{\frak{R}} _S({\cal H})]\le \sqrt{\frac{r ^2 \Lambda ^2}{m}}$$

注意到上界是一个和特征空间 $\cal X$（的维度）无关的式子，具体后面会讨论

证明：
$\widehat{\frak{R}} _S({\cal H})=\frac{1}{m}\mathbb{E} _{\boldsymbol{\sigma}}[\sup _{{\Vert {\bf w}\Vert}\le \Lambda}\sum _{i=1} ^m \sigma _i {\bf w\cdot x} _i]$
提出 $\bf w$，对 ${\bf w}\cdot \sum _{i=1} ^m \sigma _i {\bf x} _i$ 用柯西不等式 Cauchy-Schwartz $\bf |a\cdot b|\le |a|\cdot |b|$：
${\bf w}\cdot \sum _{i=1} ^m \sigma _i {\bf x} _i\le \Vert{\bf w}\cdot \sum _{i=1} ^m \sigma _i {\bf x} _i\Vert\le \Vert{\bf w}\Vert\cdot \Vert\sum _{i=1} ^m \sigma _i {\bf x} _i\Vert\le \Lambda\Vert\sum _{i=1} ^m \sigma _i {\bf x} _i\Vert$
$\mathbb{E} _{\boldsymbol{\sigma}}[\Vert\sum _{i=1} ^m \sigma _i {\bf x} _i\Vert]=\mathbb{E} _{\boldsymbol{\sigma}}[\sqrt{\sum _{i=1} ^m \sum _{j=1}^m \sigma _i\sigma _j {\bf x} _i\cdot {\bf x} _j}]=\mathbb{E} _{\boldsymbol{\sigma}}[\sqrt{\sum _{i\ne j} \sigma _i\sigma _j {\bf x} _i\cdot {\bf x} _j + \sum _{i=1} ^m \Vert{\bf x} _i\Vert ^2}]$，考虑把 $\mathbb{E}$ 塞进根号里就能去掉 $\sum _{i\ne j}$，考虑 Jensen 不等式：凸函数 $f$ 有 $f(\mathbb{E}[X])\le \mathbb{E}[f(X)]$，取 $f$ 为平方，则原式的平方小等于 $\mathbb{E} _{\boldsymbol{\sigma}}[{\sum _{i\ne j} \sigma _i\sigma _j {\bf x} _i\cdot {\bf x} _j + \sum _{i=1} ^m \Vert{\bf x} _i\Vert ^2}]=\mathbb{E} _{\boldsymbol{\sigma}}[{\sum _{i=1} ^m \Vert{\bf x} _i\Vert ^2}]\le mr ^2$，代入得到 $\Lambda \sqrt{m r ^2}/m=\sqrt{r ^2\Lambda ^2 / m}$

合并该定理和上述两种定理，分别得到：

Th. Margin bound, bounded weight vectors case
容量为 $m$ 的样本 $S\sube \{{\bf x:\Vert x\Vert}\le r\}$，假设集合 ${\cal H}=\{{\bf x\mapsto w\cdot x:\Vert w\Vert}\le \Lambda\}$，则

1. 固定置信间隔 $\rho>0$，以至少 $1-\delta$ 的概率，对任意 $h\in \cal H$ 有：

$$R(h)\le \widehat{R} _{S,\rho}(h) + \frac{2}{\rho}\sqrt{\frac{r ^2 \Lambda ^2}{m}}+\sqrt{\frac{\log \frac{1}{\delta}}{2m}}$$

2. 对于该固定的 $r>0$，以至少 $1-\delta$ 的概率，对任意 $h\in \cal H,\rho\in (0,r]$ 有：

$$R(h)\le \widehat{R} _{S,\rho}(h) + \frac{4}{\rho}\sqrt{\frac{r ^2 \Lambda ^2}{m}}+\sqrt{\frac{\log \log _2 \frac{2r}{\rho}}{m}} +\sqrt{\frac{\log \frac{2}{\delta}}{2m}}$$

观察式子，这个上界只和分类面 margin 有关，即对样本的分类惩罚项 $\widehat{R} _{S,\rho}(h)$ 和 $r\Lambda/\rho$ 项。对于线性可分情况，记当前分类面的几何距离为 $\rho _\text{geom}$，令 $\rho=\rho _\text{geom}$，则分类惩罚项为零，对于后一项显然令几何距离越大越好，这就是 SVM 算法来由的理论保障
此外，我们曾经提到过泛化误差的下界是关于特征空间 $\cal X$ 及其分布的式子，而这个定理给的上界看起来与之无关。实际上这并不矛盾，因为下界的叙述是对于总是存在的那个不好的分布 $\cal D$ 而言的，而这种分布下，上界会因为巨大的经验误差 $\widehat{R} _{S,\rho}(h)$ 变得很松；因此，即使上界从式子上看起来无关，是否存在一个好的分类面（从而使得经验误差足够小）却是和特征空间的分布有关的