高等数学A2 2020/4/14 第十五次课

返回主索引

多元函数的求导法则

多元函数与多元函数的复合

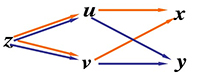
\(z=f(u,v)\;\;\) \(\;\;\begin{cases}u=\varphi (x,y)\\v=\psi (x,y)\end{cases}\) 均可偏导

于是 \(z=f[\varphi (x,y),\psi (x,y)]=z(x,y)\)

\(\begin{cases}\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}·\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}·\frac{\partial v}{\partial x}\\\;\\\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}·\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}·\frac{\partial v}{\partial y}\end{cases}\;\;\;\) （链式法则）

多元函数与一元函数复合

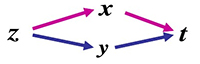
\(z=f(x,y)\;\;\;\;\begin{cases}x=\varphi (t)\\y=\psi (t)\end{cases}\) 均可导

于是 \(z=f[\varphi (t),\psi (t)]=z(t)\)

全导数 \(\frac{dz}{dt}=\frac{\partial z}{\partial x}·\frac{dx}{dt}+\frac{\partial z}{\partial y}·\frac{dy}{dt}\)

一元函数与多元函数复合

\(z=f(u)\) 可导 \(\;\;y=\varphi (x,y)\) 可偏导

于是 \(z=f[\varphi (x,y)]=z(x,y)\)

\(\frac{\partial z}{\partial x}=\frac{dz}{du}·\frac{\partial u}{\partial x}=f'(u)·\frac{\partial u}{\partial x}\)

\(\frac{\partial z}{\partial y}=\frac{dz}{du}·\frac{\partial u}{\partial y}=f'(u)·\frac{\partial u}{\partial y}\)

提示

\((1)\) 具体的函数不妨先复合再求导
\((2)\) 抽象函数的导数依照以上规则处理

多元复合函数的全微分

\((1)\;z=f(x,y)\)

\(\;\;dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}·dy\;\;\)（\(x,y\) 为自变量）

\((2)\;z=f(u,v)\;\;\) \(\;\;\begin{cases}u=\varphi (x,y)\\v=\psi (x,y)\end{cases}\)

\(dz=(\frac{\partial z}{\partial u}·\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}·\frac{\partial v}{\partial x})dx+(\frac{\partial z}{\partial u}·\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}·\frac{\partial v}{\partial y})dy\)

\(\;\;\;\;\,=\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv\;\;\)（\(u,v\) 为中间变量，服从全微分形式的不变性）