高等数学A2 2020/3/12 第六次课

返回主索引

向量及其线性运算

• 单位向量：与非零向量 \(\vec a\) 同向的单位向量记做：\(\vec{a^0}\;\) 或 \(\;\vec {e_a}\) 为 \(\;\vec a\;\)单位化的结果

• 位置向量：向量 \(\vec r\) 满足 \(\vec r = \vec{OM}\) 则称其为点 \(M\) 的位矢，由向量自身变化形成的函数 \(r=r(t)\) 称为向量函数

• 向量的加减法：满足结合律，交换律

• 常数乘向量：满足消去律 \(|k\vec F|=|k|·|\vec F|\;\;\;\;k(\vec a + \vec b)=k\vec a + k\vec b\)

• 平面象限 \((x,y)\)（右手系）：\(Ⅰ(+,+)\;\;\;\;Ⅱ(-,+)\;\;\;\;Ⅲ (-,-)\;\;\;\;Ⅳ (+,-)\)

• 空间卦限 \((x,y,z)\) （右手系）：

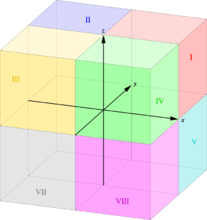
\(Ⅰ(+,+,+)\;\;\;\;Ⅱ(-,+,+)\;\;\;\;Ⅲ (-,-,+)\;\;\;\;Ⅳ (+,-,+)\)

\(Ⅴ (-,+,-)\;\;\;\;Ⅵ (+,-,-)\;\;\;\;Ⅶ (-,-,-)\;\;\;\;Ⅷ (+,-,-)\)

• 向量线性运算：即向量分量的运算 \((2,3,3)+(3,2,2)=(5,5,5)\)

• 向量平行：\(\vec{a}∥\vec{b}\Leftrightarrow \frac{a_1}{b_1}=\frac{a_2}{b_2}=\frac{a_3}{b_3}\)

• 空间两点距离：\(d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}\)

• 向量的方向余弦：一个向量的三个方向余弦分别是这向量与三个坐标正半轴之间的角度的余弦。两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。

\(\;\;\;\;cosα=\frac{x}{|\vec a|}\;\;\;\;cosβ=\frac{y}{|\vec a|}\;\;\;\;cosγ=\frac{z}{|\vec a|}\)

\(\;\;\;\;\vec{e_a}=(cosα,cosβ,cosγ)=(\frac{x}{|\vec a|},\frac{y}{|\vec a|},\frac{z}{|\vec a|})\)

\(\;\;\;\;\cos^2α+cos^2β+cos^2γ=1\)

• 向量的方向角：\(\;\;\;\;α=arccos\frac{x}{|\vec a|}\;\;\;\;β=arccos\frac{y}{|\vec a|}\;\;\;\;γ=arccos\frac{z}{|\vec a|}\)