批量归一化Batch Normalization的学习
1. 是什么
想象一下,正在训练一个很深的神经网络,比如有几十层。网络的每一层都在学习如何将输入数据变换成对最终任务更有用的表示。
现在,考虑第10层。它的输入来自于第9层的输出。在训练过程中,由于反向传播和梯度下降,第1层到第9层的所有参数(权重和偏置)都在不停地更新。这意味着,对于第10层来说,它每次接收到的输入数据的分布(比如均值和方差)都在“漂移”,非常不稳定。
这就好比一个学生(第10层)在学习,但老师(前9层)教的内容和风格总是在变,这个学生就很难学好。
这个现象在学术上被称为内部协变量偏移 (Internal Covariate Shift, ICS)。
批量归一化(BN)的核心思想就是: 在每一层的输入处(激活函数之前),强行将这些不稳定的数据分布重新“拉”回到一个稳定、标准的正态分布上(即均值为0,方差为1),从而为每一层提供一个稳定的学习基础。
所以可以理解为数据的分布就是要学习的内容
2.怎么做
Training
在训练时,我们是按一小批(mini-batch)数据进行训练的。BN的操作针对的就是这一批数据。假设一个mini-batch有 m 个样本,对于一个层级的某个特征维度,其操作步骤如下:
1计算批次均值 (μ_B):计算这个mini-batch在该特征维度上的平均值。
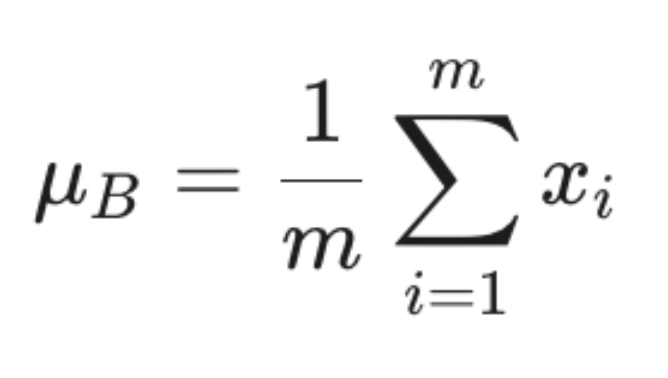
2计算批次方差 (σ_B2):计算这个mini-batch在该特征维度上的方差。
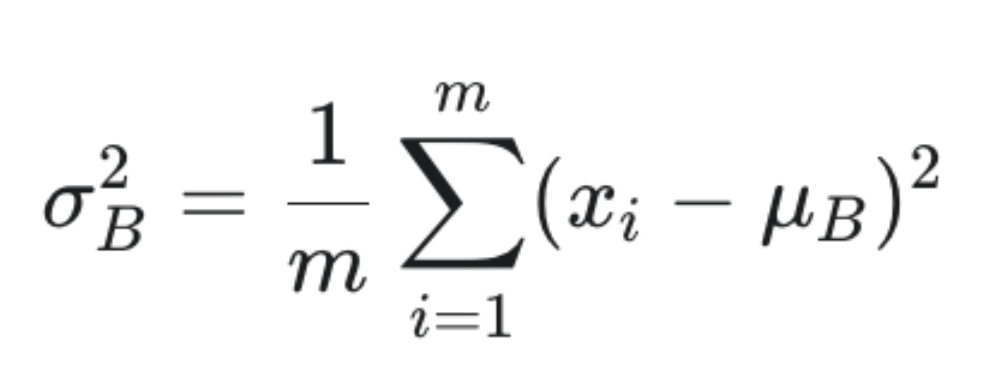
3归一化 (x_i^):使用上面计算的均值和方差,对每个样本 x_i 进行归一化。
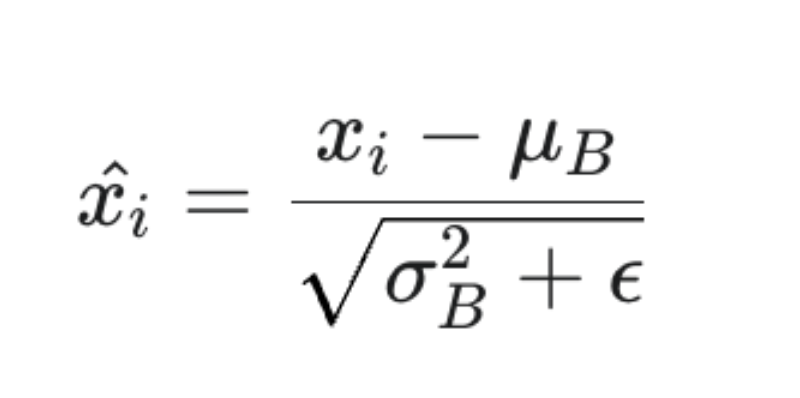
这里的 ϵ (epsilon) 是一个非常小的正数(例如 1e-5),用于防止分母为零。
4 难点 缩放和平移 (y_i):仅仅将数据归一化到标准正态分布可能会限制网络的表达能力。
这个表达能力的意思就是 网络输出值的范围,如果一直限制在0附近,那么表达能力就不太行。
例如,对于Sigmoid激活函数,我们可能不希望数据总是集中在0附近(线性区域)。
因此,BN引入了两个可学习的参数:缩放因子 γ (gamma) 和平移因子 β (beta)。
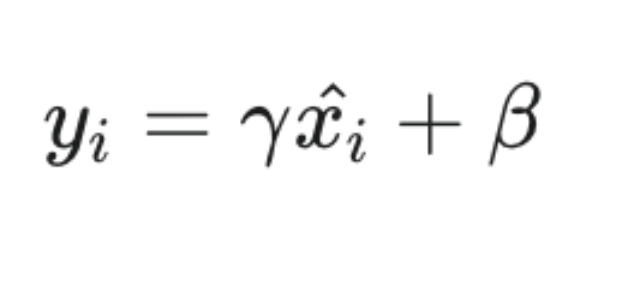
γ 和 β 与网络的其他权重一样,通过反向传播进行学习。这给了网络一个“反悔”的机会:如果标准正态分布不好,网络可以通过学习到的 γ 和 β 将数据调整到任何它认为最优的分布。
5 更新全局统计量:在训练时,BN层还会维护一个全局的均值(running_mean)和方差(running_var)。它们通过移动平均的方式,不断地汇集所有mini-batch的统计信息,为测试阶段做准备。
Inference
在测试或实际部署时,我们可能一次只处理一个样本,计算整个批次的均值和方差是不现实的。这时,在训练阶段计算并保存下来的全局统计量 running_mean 和 running_var 就派上用场了。
简单来说对每个样本就是进行使用全局统计量来直接进行归一化操作。
对于一个测试样本 x,其BN操作为:
-
归一化:使用全局统计量进行归一化。
![image]()
-
缩放和平移:使用训练好的 γ 和 β 参数。
![image]()
3advantage
-
加速训练:通过稳定每层输入的分布,使得网络可以用更大的学习率进行训练,从而加速收敛。
-
降低对权重初始化的敏感度:BN的存在使得网络对初始参数的选择不再那么苛刻。
-
自带正则化效果:由于每个mini-batch的统计量都有一些噪声,这为网络的学习过程引入了随机性,类似于Dropout,可以在一定程度上防止过拟合。
-
防止梯度消失/爆炸:将数据维持在一个合理的范围内,有助于避免激活函数进入饱和区,从而缓解了梯度问题。
具体介绍:
1没有BN时的问题:
用一个具体的例子来说明:
想象一下,我们要训练一个神经网络来完成一个多工序的任务,比如一个“机器人组装生产线”。
-
机器人A (第1层):负责在底座上打一个孔。
-
机器人B (第2层):负责将螺丝拧入A打的孔中。
-
机器人C (第3层):负责给拧好螺丝的底座喷漆。
-
...
-
机器人Z (最后一层):负责质检,判断产品是否合格。
在训练开始时,所有机器人都是学徒,它们需要同时学习和调整自己的动作。
问题1 内部协变量偏移 (Internal Covariate Shift) - “下游工友的噩梦”
这个问题是所有问题的根源。
场景描述:
-
第一次尝试 (Batch 1):
-
学徒机器人A经验不足,把孔打偏了2毫米。
-
学徒机器人B为了完成任务,费了很大劲,学会了如何针对这个偏了2毫米的孔去拧螺丝。它调整了自己的机械臂角度和力度,最终成功了。
-
学徒机器人C也学会了给这个拧好螺丝的、孔位不正的底座喷漆。
-
-
第二次尝试 (Batch 2):
-
机器人A收到了反馈(反向传播的梯度),知道了上次的孔打偏了。于是它自我修正,这次把孔打在了完美的中心位置!
-
现在轮到机器人B了。它傻眼了。它刚刚学会的“如何处理偏2毫米的孔”这套精妙的动作,现在完全没用了。输入给它的工件(带孔的底座)和上次完全不一样了。它面对的是一个全新的任务。
-
机器人B不得不抛弃刚学到的技巧,重新学习如何处理这个位于中心的孔。这个过程可能导致它矫枉过正,动作幅度非常大,结果把螺丝拧坏了。
-
机器人C就更崩溃了,因为B的输出也变得和上次完全不同。
-
这就是内部协变量偏移的本质:
对于网络中的任何一层(比如机器人B),它的工作表现不仅取决于自己,更严重地依赖于它所有上游层(机器人A)的输出。
在训练中,上游层的参数在不断更新,导致其输出数据的分布(均值、方差等)也在剧烈变化。
这会直接导致:
-
学习效率极低:下游层(机器人B、C)无法稳定地积累经验,因为它们的工作前提总是在变。它们大部分时间都花在了“适应上游的变化”上,而不是“提升自己的技能”。
这个是关键,每一层都需要学习自己的知识经验,但是学习都是基于上一层的工作前提,如果工作前提一直在变,也就是上游层的参数一直在改变,那么模型的时间都花在适应上一层参数的变化上了。 -
需要极小的学习率:为了不让整个生产线崩溃,总指挥(优化器)只能让每个机器人都进行非常微小的调整(很小的学习率)。如果机器人A一次性调整太多,机器人B可能就彻底“罢工”了(损失函数爆炸)。
这个就是为什么这种问题需要很小的学习率,所以学习效率低。
问题二:对初始化的极端敏感 - “开工第一天的赌博”
场景描述:
生产线开工第一天,我们需要给所有机器人设置一个初始状态(权重初始化)。
-
情况A:初始化权重过大
-
我们给机器人A设置了一个“过度用力”的模式。它打孔时,力量巨大,不仅打穿了底座,还把底座打出了裂缝。
-
这个带有裂缝的、夸张的“特征”被传递给机器人B。机器人B的动作也被放大了,它拧螺丝时可能直接把底座拧碎了。
-
到了机器人Z那里,它看到的是一堆碎片。它给出的反馈信号(梯度)会非常极端,这就是“梯度爆炸”。
-
-
情况B:初始化权重过小
-
我们给机器人A设置了一个“畏手畏脚”的模式。它打孔时,力量太小,只在底座上留下了一个浅浅的凹痕。
-
这个微弱的“特征”传递给机器人B,B可能根本识别不到这个凹痕,于是它什么也没做。
-
到了机器人Z那里,它看到的是一个几乎没变化的底座。它给出的反馈信号会极其微弱,近乎为零。这个信号传回给机器人A时,已经衰减没了。这就是“梯度消失”。
-
没有BN的网络,就像这个脆弱的生产线: 它要求“开局”必须设置得恰到好处。初始参数稍微有点偏差,其影响就会在深层网络中被指数级放大,导致整个学习过程在开始时就陷入瘫痪。
问题三:梯度消失 - “声音无法传达到前线”
这个问题与激活函数(如Sigmoid)的饱和区密切相关。
场景描述:
想象一下,生产线的机器人之间通过对讲机沟通反馈。
-
对讲机的特性 (Sigmoid函数):这个对讲机很奇怪,只有在音量适中时,声音才清晰。如果声音太大或太小(进入饱和区),对讲机输出的声音都会变得非常微弱,几乎听不见(梯度接近0)。
参考sigmoid函数 这里实际上对讲机输出声音就是梯度 -
没有BN时的工作流程:
-
机器人C在工作时,由于上游机器人A和B传递过来的工件特征值非常大(比如数值>10),这相当于它对着对讲机在大吼。(正向传播)
-
根据对讲机的特性,虽然输入声音很大,但输出的声音却极其微弱(梯度接近0)。(激活函数)
-
当最终的质检员Z想把“产品不合格”这个重要的反馈信息传回给A时,这个信息需要经过C、B的对讲机。(反向传播)
-
信息传到C这里,C的对讲机因为输入饱和,输出的声音变得微弱。
-
这个微弱的声音再传给B,B的对讲机可能也因为输入饱和,输出的声音变得更加微弱。
-
等这个反馈信息传到机器人A那里时,已经变成了几乎听不见的“电流声”。
-
这就是梯度消失的本质: 由于没有BN来控制每层输入激活函数的数据范围,数据很容易就进入激活函数的“饱和区”(对讲机的失真区)。在反向传播时,梯度每经过一个饱和的激活函数,就会被乘以一个接近0的数,导致梯度信号在层层回传中迅速衰减。
饱和的激活函数就是该层的输入过大或者过小。
最终结果是: 网络的前几层(机器人A、B)几乎接收不到任何有效的反馈信号,它们的参数常年得不到更新,学不到任何东西。整个深度网络,实际上只有靠近输出的最后几层在学习,名存实亡。
总的理解就是,在前向传播中,都传的过来。但是在前向传播中,输入x的值过大或者过小,都会让该层的梯度接近0,则在反向传播时,上游的梯度传到这些层的时候,都会乘上0,则这些层的梯度就消失了。所以只有靠近输出的最后几层有梯度,前面几层的梯度几乎都是0.
2有BN的情况
1 加速训练 允许使用更高的学习率
BN层就像在每一层都设置了一个“数据分布稳定器”。
-
稳定是关键:无论前面几层如何“天翻地覆”,BN层都会“粗暴”地将输入数据拉回到一个标准的、稳定的分布上(均值为0,方差为1附近)。
-
学习环境改善:现在,对于第90层来说,它看到的输入数据分布基本是稳定的。就像一个学生,虽然老师换了好几个,但教材(数据分布)是统一的。
-
解放学习率:因为输入分布稳定了,第90层就不再那么害怕前面层参数变化带来的剧烈影响。它有了“安全感”,可以更大胆地更新自己的参数。因此,我们可以设置一个更大的学习率,模型的收敛速度自然就大大加快了。
比喻: 训练一个没有BN的深层网络,就像试图在一个持续地震的沙滩上盖一座高楼。你必须非常缓慢和小心。而BN就像为每一层都打下了一个坚固的混凝土桩基,让盖楼的过程变得又快又稳。
2降低对初始化的敏感度
BN层是“数值范围的守护者”。
-
重置作用:无论上一层的线性变换(
W*x + b)因为糟糕的初始化输出了多么离谱的数值(可能非常大,也可能非常小),BN层都会将其“一视同仁”地进行归一化,强行拉回到均值为0,方差为1的范围。 -
解耦依赖:这相当于切断了每一层对前一层权重大小的强依赖关系。即使初始权重不太理想,BN也能在很大程度上“拯救”它,保证传递给下一层的数据是分布良好、数值健康的。
比喻: 没有BN的网络就像一长串多米诺骨牌,第一块骨牌(初始化)必须推得恰到好处,力量太大或太小都会导致整串骨牌无法正常倒下。而BN就像在每两块骨牌之间都放了一个自动重置装置,无论前一块骨牌以多大的力量倒过来,这个装置都会用一个标准的力量去推动下一块骨牌。
3自带正则化效果
1. 什么是正则化?
简单来说正则化就是引入随机性,提升鲁棒性。
而鲁棒性就是 系统、模型或算法在面对输入数据、环境或参数的扰动时,仍能保持其性能的稳定性和可靠性的能力。
正则化的目的是防止模型过拟合。过拟合就是模型太“死记硬背”训练数据了,以至于对新的、没见过的数据泛化能力很差。常用的正则化方法(如Dropout)通过在训练中引入随机性来迫使模型学习更鲁棒的特征。
2. BN如何实现正则化?
BN的正则化效果来自于它的一个核心机制:使用mini-batch的均值和方差进行归一化。
-
批次噪声:在训练时,每次我们都只取一小批数据(比如64张图片)来计算均值和方差。由于批次是随机抽取的,这个批次的均值和方差会和下一个批次的均值和方差有细微的差别。
-
随机扰动:这意味着,对于同一个训练样本,当它被分到不同的mini-batch中时,它被归一化后的值是略有不同的。因为用来归一化它的“尺子”(批次均值和方差)每次都不同。
-
强迫模型学习本质:这种微小的、随机的扰动,对模型来说就是一种噪声。模型为了在这种噪声下依然能做出正确的判断,就不能过分依赖输入数据中某个特定的数值,而必须去学习更本质、更通用的特征。这自然就起到了防止过拟合的正则化效果。
比喻: 这就像教一个孩子认苹果。如果你每次都只给他看一张一模一样的、完美无瑕的红苹果照片,他可能会认为“只有长这样的才是苹果”。但如果你每次给他看的照片都有轻微的不同(光线、角度、背景略有变化),他为了能认出来,就必须学会抓住“苹果”这个概念的核心特征(形状、颜色范围、质感等),而不是死记硬背某张照片。BN的批次噪声就扮演了这种“轻微变化”的角色。
4防止梯度消失/爆炸
BN层通常放在激活函数之前。
-
拉回中心区域:BN将输入数据归一化到均值为0,方差为1的范围。对于Sigmoid或tanh这类激活函数,这个范围正好是它们梯度最大、最“活跃”的中心线性区域。
-
保持梯度流动:通过强制让大部分数据落在激活函数的非饱和区,BN保证了梯度能够以一个健康的幅度进行反向传播,不容易在某一层突然变得过小或过大。这就有效缓解了梯度消失和爆炸的问题,让梯度能够“流”得更深,训练更深的网络成为可能。
比喻: 激活函数就像一个通信管道。管道的两端非常狭窄(饱和区),中间部分很宽阔(非饱和区)。没有BN,数据可能随意地涌向狭窄的两端,导致信息(梯度)无法通过。BN就像一个“交通协管员”,把所有的数据都引导到宽阔的中间道路上,确保交通(梯度流)顺畅。
4Code
前向传播
第一件事,先判断是不是第一次运行,判断依据为看gamma参数是否为None,如果是,这说明是第一次运行,需要给参数初始化。
初始化参数:
self.gamma=np.ones(D)
self.beta=np.zeros(D)
self.running_mean=np.zeros(D)
self.running_var=np.ones(D)
D为输入x的第二维度,特征数。
由y=gamma*x_norm+beta这个缩放平移公式
初始化时,gamma初始化为全1 beta初始化为全0 代表刚开始 不缩放 也不平移
全局均值
而全局均值和全局方差的初始化比较难,接下来分析一下。
将 self.running_mean 初始化为0,self.running_var 初始化为1,是因为这代表了标准正态分布(均值为0,方差为1)的统计特性。这是一种最“中性”、最“无偏”的初始假设,可以看作是网络在看到任何真实数据之前,对数据分布的一个标准化的“默认猜测”。
为什么呢?
1最合理的“无信息”先验 (Uninformative Prior)
在模型开始训练之前,我们对整个数据集的真实分布一无所知。选择 均值为0,方差为1 作为初始值,是基于标准正态分布做出的最合理、最通用的假设。
- 均值为0:假设数据在中心点是平衡的,没有任何预设的偏移或偏置。这是一个对称的、不偏不倚的起点。
- 方差为1:假设数据具有一个标准的、单位化的尺度或“胖瘦”。方差不能为0(会导致除零错误),而设为1则是一个最基础、最标准的尺度单位。任何其他值(如0.1或10)都意味着我们预先假设数据的分布非常集中或非常分散,而我们并没有依据做这样的假设。
2作为移动平均的起点
这两个值是指数移动平均的起始点。让我们看看第一次训练迭代时会发生什么:
-
running_mean的第一次更新:new_running_mean = momentum * 0 + (1 - momentum) * first_batch_mean -
running_var的第一次更新:new_running_var = momentum * 1 + (1 - momentum) * first_batch_var
可以看到,这个初始值 (0, 1) 在第一次更新后,就会立刻被第一个批次的真实统计数据“拉”向真实的方向。它只是提供了一个计算的起点,而 (0, 1) 是最稳健、最符合“归一化”思想的起点。
前向传播的时候,训练模式和推理模式有区别,参考前面的原理,关键就是在训练阶段要做两件事,更新全局均值、方差和缓存中间变量用于反向传播。
#4 更新全局均值和方差 (使用移动平均)
self.running_mean=self.momentum*self.running_mean+(1-self.momentum)*batch_mean
self.running_var=self.momentum*self.running_var+(1-self.momentum)*batch_var
#5 缓存中间变量以备反向传播
self.cashe=(x,x_norm,batch_mean,batch_var,self.gamma)
移动平均,就是使用EMA来更新参数,参考[[SMA和EMA]]
反向传播:
重点难点!!
第一层参数的梯度
前向传播的输出公式为
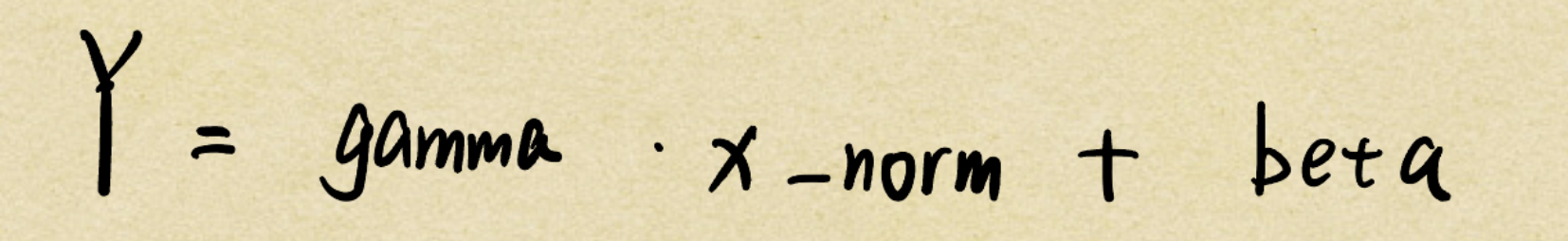
则先求dgamma 也就是损失L对gamma的梯度
由链式法则

则目标就是在这个前向传播的公式中 求Y对gamma的偏导 由偏导公式易得出
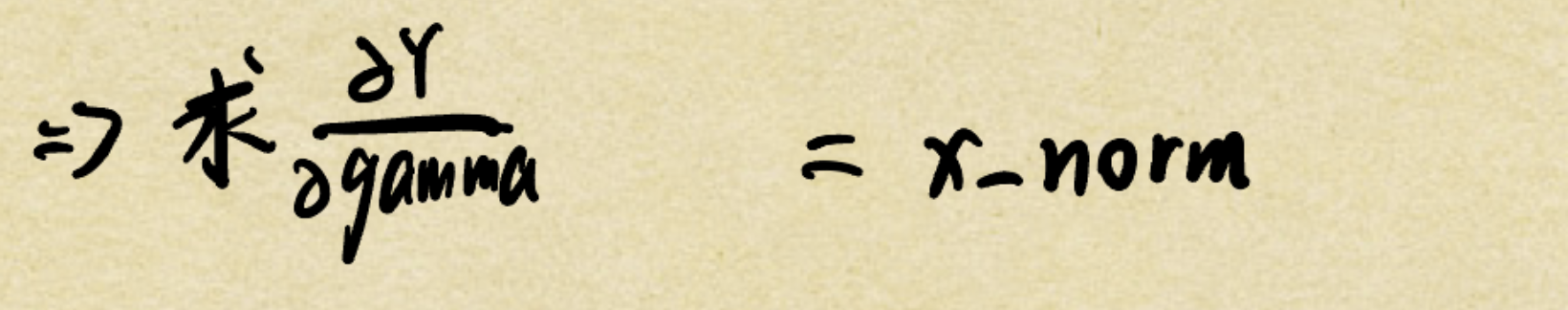
所以由链式法则:
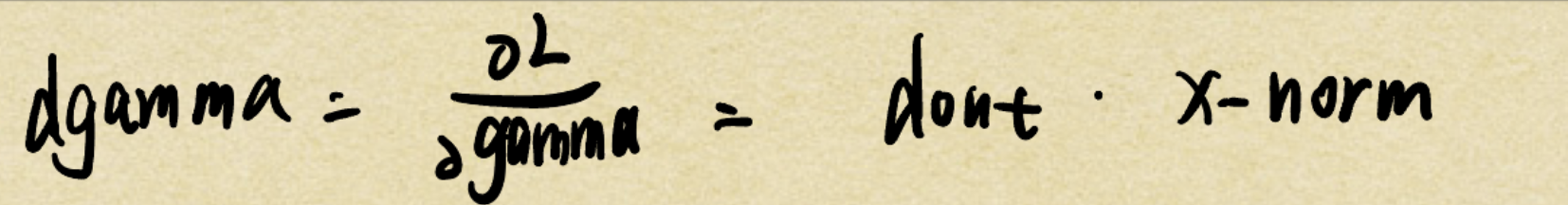
但是分析形状:
dout[bs,D] x_norm[bs,D]
看起来形状并不匹配,不能做矩阵乘法运算。但是这里就涉及到知识点:[[前向决定反向]]
所以这里做的是元素相乘 运算结果形状仍然为dgamma[bs,D]
此时还需要对dgamma做第一个维度(axis=0)上的求和操作(np.sum)
原因可以用两个理解:
在整个网络中,gamma 是一个可学习的参数 (Parameter),它的作用是独立地缩放每一个特征维度。关键在于,对于一个批次(Batch)里的所有样本(比如 N=32 个样本),它们共享同一套 gamma 参数。
- 直观比喻:一个政策如何影响一个省
-
gamma:可以看作是一项省级政策,比如“全省所有企业减税5%”。这项政策只有一个,就是gamma这个向量。 -
特征维度
D:假设省里有D个不同的行业(IT、制造、餐饮等)。gamma向量的每一个元素gamma[j]就是针对第j个行业的具体减税政策。 -
一个批次
N:可以看作是省里随机抽查的N家企业。 -
损失
L:可以看作是衡量全省经济健康程度的指标。
现在,我们要评估“减税政策 (gamma)”对“全省经济 (L)”的影响有多大(也就是求梯度)。
减税政策 gamma[j](比如针对IT行业的减税)会同时影响到我们抽查的所有 N 家企业中的IT业务部分。它会影响企业A的IT业务,也会影响企业B的IT业务,...,一直到第N家企业。
因此,要计算这项政策对全省经济的总体影响,我们不能只看它对某一家企业的影响,而必须把它对所有 N 家企业的影响全部累加起来。
这就是“求和”的本质:把一个共享参数在所有样本上产生的影响梯度进行汇总。
- 从数学和形状的角度解释(简单直观)
现在求的是dgamma 则形状要和gamma一样 所以要去掉第一个维度 所以对第一个维度做sum操作即可。
dgamma=np.sum(dout*x_norm,axis=0)
同理 dbeta易得:

所以一样需要做求和操作
dbeta=np.sum(dout,axis=0)
同理 dx_norm易得
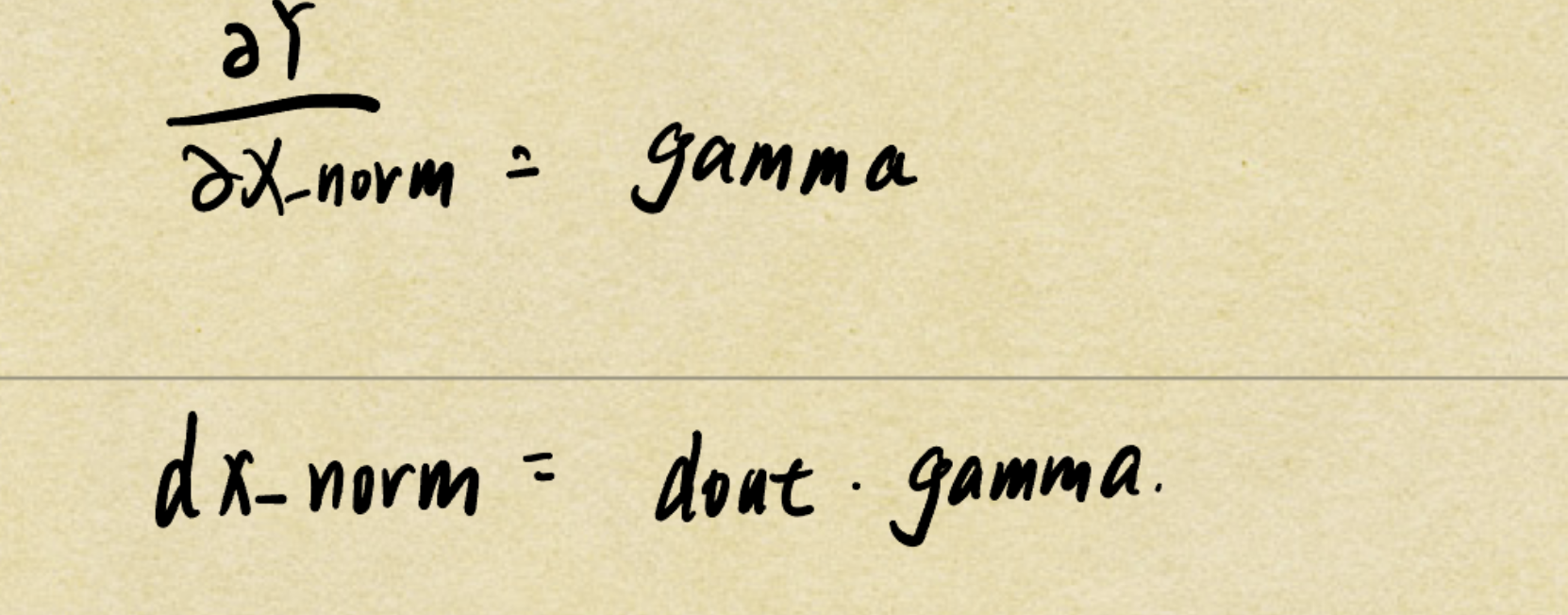
运用了广播机制 所以dx_norm的形状就是(bs,D) 符合形状,所以不需要修改。
第二层参数的梯度
为什么称为第一层,第二层
因为x_norm并不是该层的输入,是正则化后的输入,我们还需要求dx 才是最重要的梯度,称为第二层。
分析x-->x_norm的公式
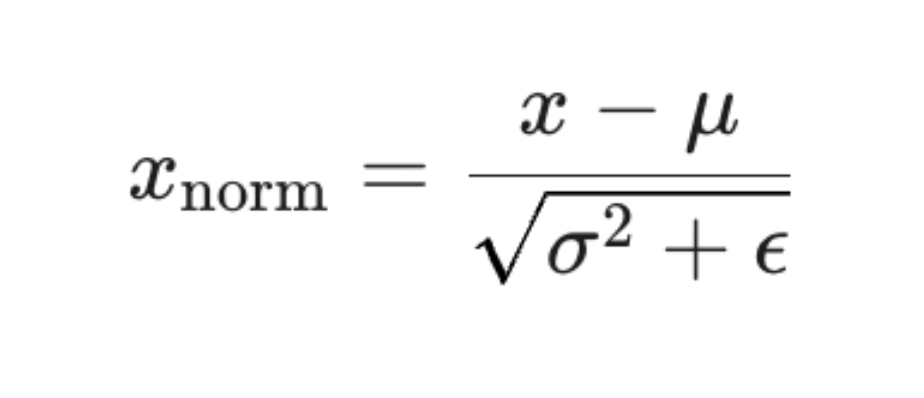
所以三个偏导数为:

这三个公式计算出的梯度被称为局部梯度 (Local Gradients)。在完整的 BN 反向传播算法中,情况会更复杂,因为 μ 和 σ2 本身也是由输入 x 计算得来的。
先实现dvar的计算
由链式法则
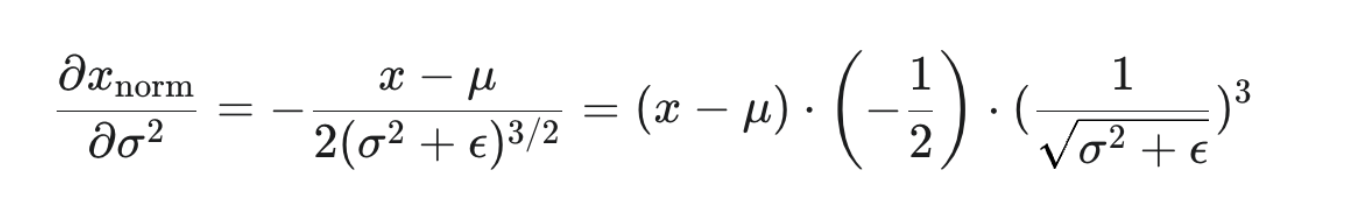
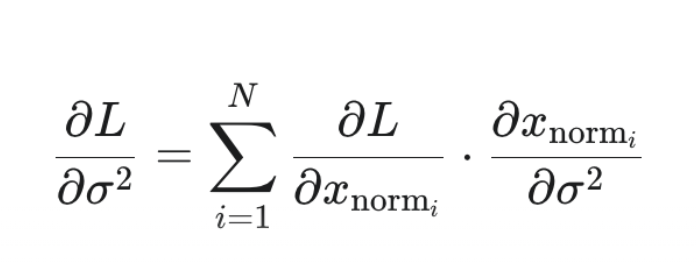
这里为什么要加求和符号,可以类比上面的dgamma,但是用形状不好判断,可以从[[聚合参数]]学习到原因。
所以我们只需要根据链式法则公式 带入参数即可:
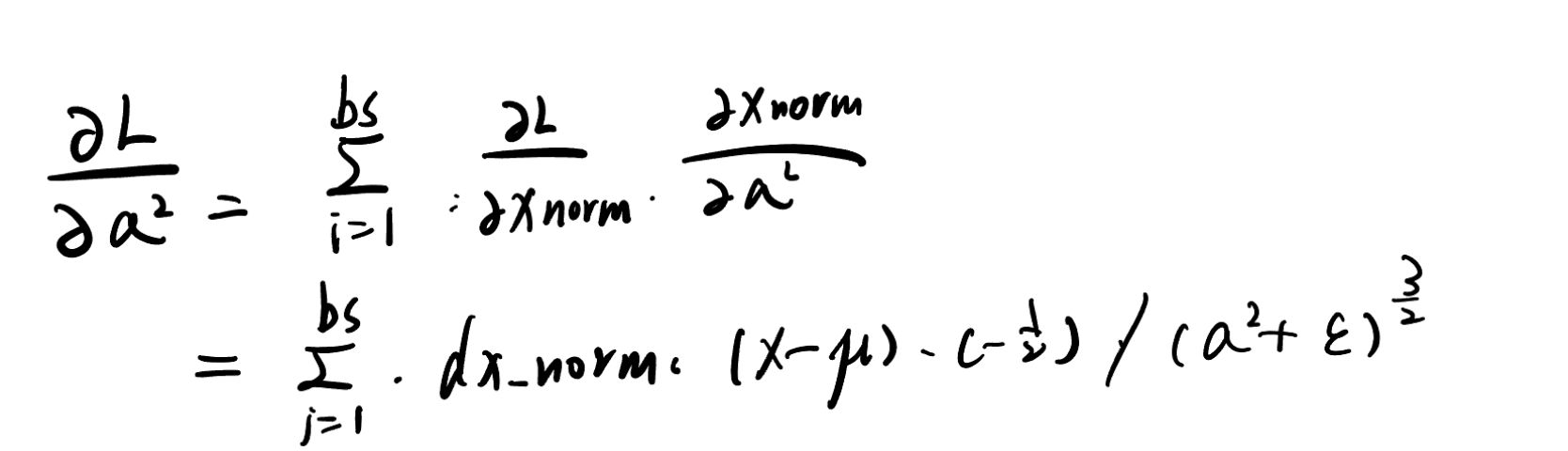
code实现为
这里要注意的一个重点是 聚合参数求梯度时候 要先求出后面的结果 再做求和操作(np.sum(axis=0))
所以code实现为
dvar_temp=dx_norm*(x-batch_mean)*(-1.0/2)/(batch_var+self.epsilon)**1.5
dvar=np.sum(dvar_temp,axis=0)
同理 dvar的梯度为

dmean_temp=dx_norm*(-1)/(batch_var+self.epsilon)**(0.5)
dmean=np.sum(dmean_temp,axis=0)
计算最终损失 L 对输入 x 的总梯度 dx 时,需要将 x 通过三条路径对 L 造成的影响全部累加起来:
-
x 直接改变 xnorm 带来的影响。
-
x 改变了均值 μ,进而改变了 xnorm 带来的影响。
-
x 改变了方差 σ2,进而改变了 xnorm 带来的影响。
因为x_norm对x求导的话,实际上mean var 都是由x得来的 则他们都是x的复合函数
所以dx:
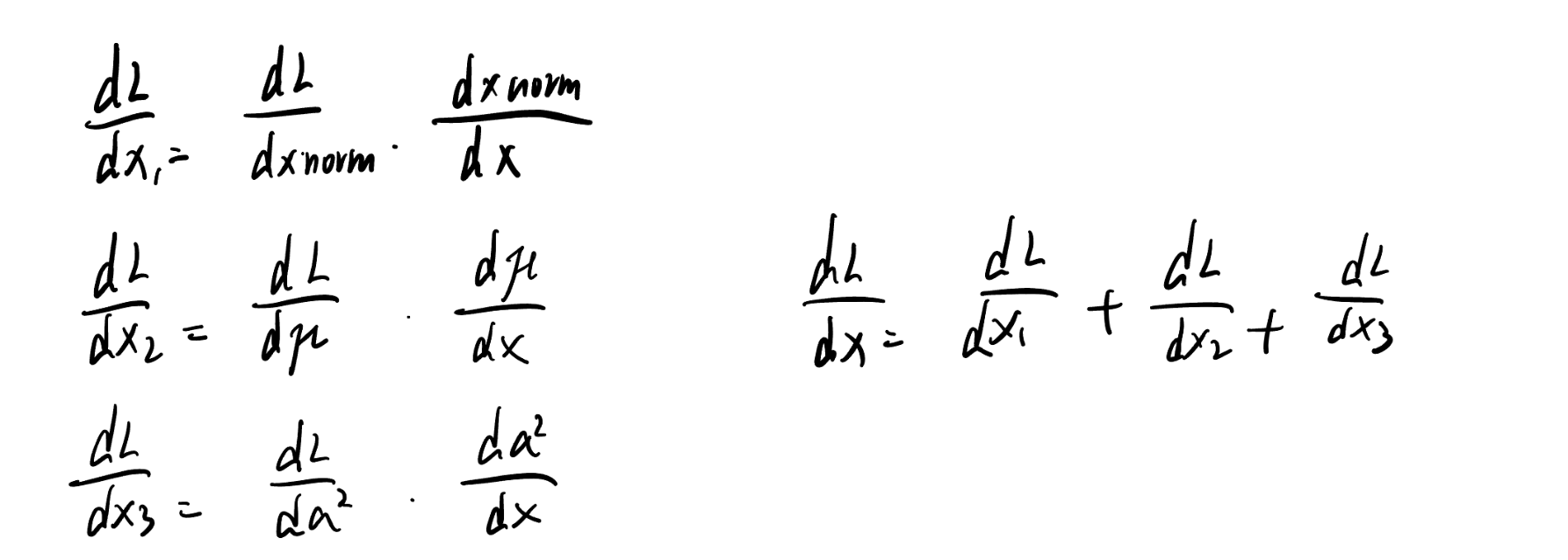
由三条路径组成 而后面两个梯度为
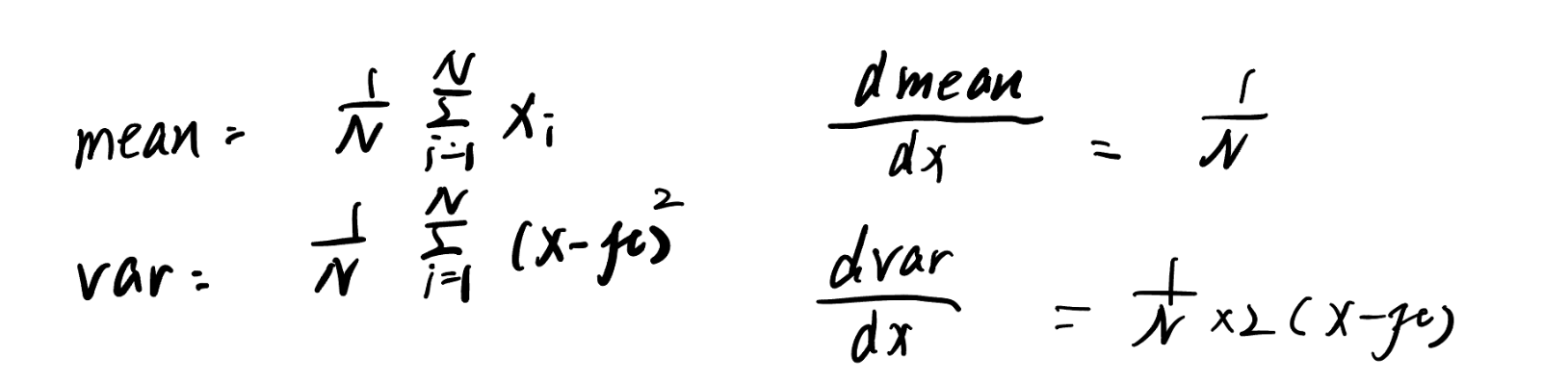
则code实现为:
dx1=dx_norm/np.sqrt((batch_var+self.epsilon))
dx2=dmean/bs
dx3=dvar/bs*2*(x-batch_mean)
dx=dx1+dx2+dx3
所以我们求dmean dvar的目的 其实就是因为要求dx的其他两个路径
5思考
为什么需要缩放和平移呢,如果只是简单的强制归一化到(0,1) 则可能会破坏网络在前一层学习到的有用信息,反而限制了模型的性能。gamma 和 beta 这两个可学习的参数,给了网络一个“反悔”的机会,让它可以自己决定最佳的输出数据分布。简单来说,缩放(gamma, γ)和平移(beta, β)是为了恢复和保留网络的原始表达能力(Representational Power)。
分析只归一化会遇到的问题:
1. 破坏了学习到的特征分布
可能前一层网络费尽心思学习到的特征,其分布的均值和方差本身就包含了重要的信息。例如,某个特征的方差较大可能代表了它的区分度很高。如果BN层强行将所有特征的分布都“捏”成完全一样的标准正态分布,就可能丢失这些有用的信息,降低了网络的表达能力。
2. 限制了激活函数的作用
这是最致命的一点。考虑一下常用的 Sigmoid 或 Tanh 激活函数。
-
Sigmoid 函数在
x=0附近的区域近似于一个线性函数。 -
在
x远离0的区域(饱和区),它才表现出强大的非线性能力,而这正是深度网络强大的原因。
如果我们将每一层的输入都严格限制在均值为0,方差为1的分布,那么大部分数据点都会落在 [-2, 2] 这个区间内,正好是 Sigmoid 函数的线性区域。这意味着激活函数基本退化成了一个线性变换,整个深度网络的能力会大打折扣,因为它无法再学习复杂的非线性映射。
网络可能需要将某些输入推向饱和区来做出决策,但强制的归一化剥夺了它这个能力。
分析两个参数具体作用
这两个参数的作用是:
-
gamma(γ):负责缩放 (scale),它可以控制输出分布的方差(胖瘦)。 -
beta(β):负责平移 (shift),它可以控制输出分布的均值(左右位置)。
最关键的是,gamma 和 beta 是通过反向传播学习到的参数,就像网络的权重 W 和偏置 b 一样。这意味着网络可以自主地学习,以决定输出的数据分布应该是什么样的,才能让最终的损失最小。
是可学习的参数!!!




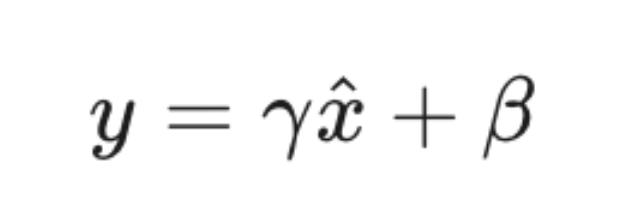

 浙公网安备 33010602011771号
浙公网安备 33010602011771号