k-means聚类入门

K-means算法

        K-均值算法是发现给定数据集的k个簇的算法，簇个数是用户给定的，每一个簇通过其质心（centroid）即簇中所有点的中心来描述。

     1、K-均值算法的流程：

        （1）对于输入样本集 {x1,x2,...,xm}，随机确定k个质心 {μ1,μ2,...,μk}；

        （2）计算每个样本xj到各个质心μi的欧式距离：dji=||xj-μi||2；

        （3）根据距离最近的μ确定样本xj的簇标记：labelj=arg minidji；

        （4）循环将数据集中的每个样本分配到各个簇中（染色），每个簇的样本数量为N1,N2,...,Nk；

        （5）更新每个簇的质心的位置，为该簇所有样本的均值；

 

 

 

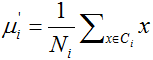
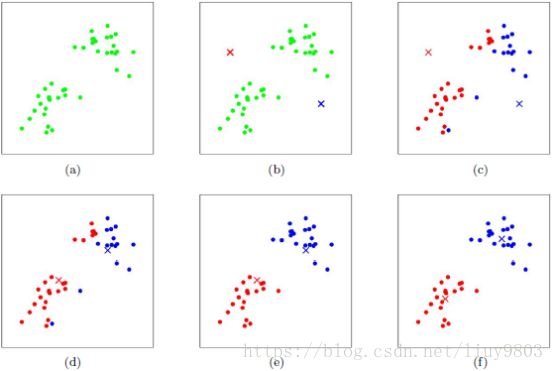
（6）重复上述步骤（染色分配-移动质心-重新染色-再次移动...），直到所有的质心均不再更新；或者达到设定的某个终止条件，如最大迭代次数、最小调整幅度阈值、最小平方误差MSE等。

K-means的优缺点

优点：

理解、实现容易；

当数据集近似高斯分布时，聚类效果非常不错；

处理大数据集的时候可以保证较好的伸缩性，时间复杂度为O(nkt)，其中n为数据集样本数量，t为迭代次数。

缺点：

k值需要调参，不同的值得到的结果不一样；

对初始质心点敏感，离群值对模型的影响比较大；

不适合非凸形状的簇、大小差别较大的簇；

可能收敛到局部极小值，在大规模数据集上收敛较慢。

K值的选择

1、样本聚类误差平方和，核心指标是SSE(sum of the squared errors，误差平方和)

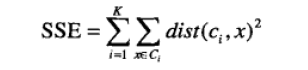
k表示k个聚类中心，ci表示第几个中心，dist表示的是欧几里得距离。
这里有一个问题就是为什么，我们更新质心是让所有的点的平均值，这里就是SSE所决定的。

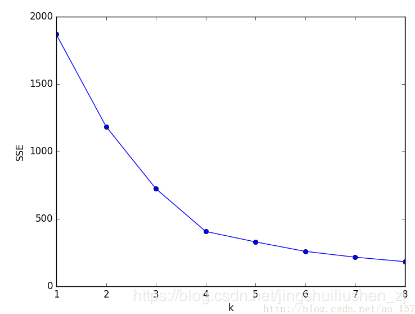
当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，这个最先趋于平缓的点就是合适的K值。

2、轮廓系数法

某个样本点X_i的轮廓系数定义如下：

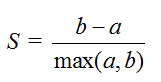
 其中，a是Xi与同簇的其他样本的平均距离，称为凝聚度，b是Xi与最近簇中所有样本的平均距离，称为分离度。而最近簇的定义是

其中p是某个簇Ck中的样本。事实上，简单点讲，就是用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后，选择离Xi最近的一个簇作为最近簇。

求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，很自然地，平均轮廓系数最大的k便是最佳聚类数。

K-means算法的改进

二分K-means算法

        为了克服K-means算法容易收敛于局部极小值的问题，可以使用bisecting K-means算法弱化随机初始质心的影响。该算法首先将所有的样本作为一个簇，然后根据某种规则将该簇一分为二；之后选择其中一个簇继续划分，直到达到停止条件（聚簇数量、迭代次数、最小SSE等）。

        选择划分聚簇的规则一般有两种：

            （1）选择样本量最大的簇进行划分；

            （2）选择SSE值最大的簇进行划分。

        伪代码如下：

            将所有样本作为一个簇

            当簇数目小于k时

                    对于每一个簇

                            计算总误差SSE

                            将给定的簇划分，对其进行k=2的K-means聚类

                            计算将该簇一分为二后的总误差

                   选择使总误差最小的那个簇进行划分操作

 

三、K-means++算法

        K-means++算法可以解决K-means对初始质心比较敏感的问题，算法的区别主要在于选择的初始k个质心的之间的相互距离要尽可能的远。

        K-means++算法的流程是：

            （1）从数据集中随机选择一个样本作为第一个质心；

            （2）对数据集中的每个样本，计算它到所有已有质心的距离的总和D(x)；

            （3）采用线性概率选择出下一个聚类中心点，即D(x)较大的点成为新增质心的概率较大；

            （4）重复步骤2直到找到k个聚类中心点

            （5）使用得到的k个质心作为初始化质心运行K-means算法。

 

        K-means++算法的缺点：

            （1）有可能选中离群点作为质心；

            （2）计算距离质心最远的点的开销比较大；

            （3）由于质心的选择过程中的内在有序性（第k个质心的选择依赖前k-1个质心的值），在扩展方面存在着性能问题。

 

四、K-means||算法

        解决K-means++算法缺点而产生的一种算法，主要思路是改变每次遍历时候的取样规则，并非按照K-means++算法每次遍历只获取一个样本，而是每次获取k个样本，重复该取样操作logm次，然后再将这些抽样出来的样本聚类出k个质心，作为K-means算法的初始质心。实践证明，一般只需要5次重复采样就可以得到比较好的初始质心。

 

五、Mini Batch K-means算法

        Mini Batch K-means算法是K-means算法的一种优化变种，采用随机抽取的小规模数据子集训练算法，减少计算时间，同时试图优化目标函数。Mini Batch K-means算法可以减少K-means算法的收敛时间，而且产生的结果一般只略差于K-means算法。

        算法步骤如下：

            （1）首先抽取数据集部分样本，使用K-means构建出k个质心的模型；

            （2）继续抽取数据集中的部分样本，将其添加到模型中，分别分配给距离最近的质心；

            （3）更新质心的位置；

            （4）循环迭代（2、3）步操作，直到质心稳定或者达到指定迭代次数，停止计算。

 

六、Canopy算法

        Canopy属于一种‘粗’聚类算法，即使用一种简单、快捷的距离计算方法将数据集分为若干可重叠的子集canopy，这种算法不需要指定k值、但精度较低，可以结合K-means算法一起使用：先由Canopy算法进行粗聚类得到k个质心，再使用K-means算法进行聚类。

        Canopy算法步骤如下：

            （1）将原始样本集随机排列成样本列表L=[x1,x2,...,xm]（排列好后不再更改），根据先验知识或交叉验证调参设定初始距离阈值T1、T2，且T1>T2 。

            （2）从列表L中随机选取一个样本P作为第一个canopy的质心，并将P从列表中删除。

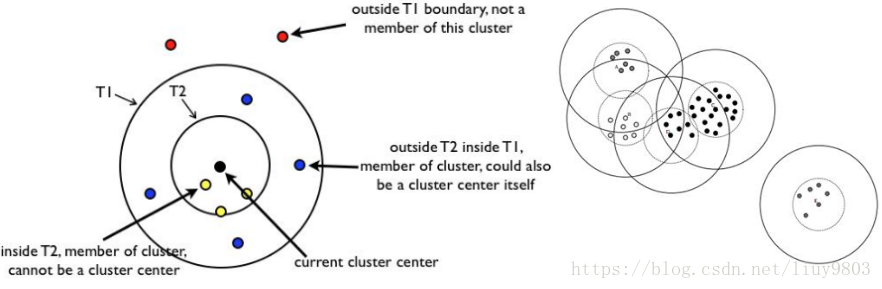
            （3）从列表L中随机选取一个样本Q，计算Q到所有质心的距离，考察其中最小的距离D：

                        如果D≤T1，则给Q一个弱标记，表示Q属于该canopy，并将Q加入其中；

                        如果D≤T2，则给Q一个强标记，表示Q属于该canopy，且和质心非常接近，所以将该canopy的质心设为所有强标记样本的中心位置，并将Q从列表L中删除；

                        如果D>T1，则Q形成一个新的聚簇，并将Q从列表L中删除。

            （4）重复第三步直到列表L中元素个数为零。

 

 注意：

            （1）‘粗’距离计算的选择对canopy的分布非常重要，如选择其中某个属性、其他外部属性、欧式距离等。

            （2）当T2<D≤T1时，样本不会从列表中被删除，而是继续参与下一轮迭代，直到成为新的质心或者某个canopy的强标记成员。

            （3）T1、T2的取值影响canopy的重叠率及粒度：当T1过大时，会使样本属于多个canopy，各个canopy间区别不明显；当T2过大时，会减少canopy个数，而当T2过小时，会增加canopy个数，同时增加计算时间。

            （4）canopy之间可能存在重叠的情况，但是不会存在某个样本不属于任何canopy的情况。 

            （5）Canopy算法可以消除孤立点，即删除包含样本数目较少的canopy，往往这些canopy包含的是孤立点或噪音点。

 

七、scikit-learn相关API

    1、生成聚类数据集的方法：

         返回产生的样本集数组X和每个样本的簇标签数组Y。

        n_samples：数据集样本总数，默认值为100个；

        n_features：每个样本的维度，默认为2维；

        centers：产生的质心点个数，默认为3个；

        cluster_std：数据集的标准差，默认值为1.0；

        center_box：质心确定后的数据边界，默认值(-10.0, 10.0)。

 2、K-means聚类算法： 

 

        返回质心数组、簇标记以及所有样本与离它最近的质心距离的平方和。

        n_clusters：k的数量，默认为8个；

        init：初始化方法，可以使用K-means++、random、或自定义的ndarray，默认使用K-means++；

        max_iter：最大迭代次数；

        tol：容忍度/阈值，即算法收敛的条件。

    3、Mini Batch K-means算法： 

     

        类似K-means。

        batch_size：数据子集的规模

        max_no_improvement：连续多少个小批量聚类计算后效果没有改善，就停止算法。默认值是10，如果不想使用这个参数可以设置为None。

初始类簇中心点的确定

1、选择批次距离尽可能远的K个点
首先随机选择一个点作为第一个初始类簇中心点，然后选择距离该点最远的那个点作为第二个初始类簇中心点，然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点，以此类推，直至选出K个初始类簇中心点。
2、 选用层次聚类或者Canopy算法进行初始聚类，然后利用这些类簇的中心点作为KMeans算法初始类簇中心点。

参考目录

机器学习之K-means、Canopy聚类：https://blog.csdn.net/liuy9803/article/details/80779692

K-means聚类最优k值的选取：https://blog.csdn.net/qq_15738501/article/details/79036255

深入理解K-Means聚类算法：https://blog.csdn.net/taoyanqi8932/article/details/53727841