K-近邻(KNN)算法
K-近邻(KNN) 作者:Yabea : https://www.cnblogs.com/ybjourney/p/4702562.html
距离度量、k值选择以及分类决策规则:https://blog.csdn.net/Daycym/article/details/81178519
KNN中的k如何选择?:https://blog.csdn.net/weixin_42234472/article/details/85062142
一文搞懂k近邻(k-NN)算法:https://zhuanlan.zhihu.com/p/25994179
KNN 算法原理
k-近邻算法(k-Nearest Neighbour algorithm)的工作原理:给定一个已知标签类别的训练数据集,输入没有标签的新数据后,在训练数据集中找到与新数据最邻近的 k 个实例,如果这 k 个实例的多数属于某个类别,那么新数据就属于这个类别。即由那些离新数据最近的 k 个实例来投票决定新数据归为哪一类。
最邻近分类算法是数据挖掘分类(classification)技术中最简单的算法之一,其指导思想是”近朱者赤,近墨者黑“,即由你的邻居来推断出你的类别。

K-近邻算法(KNN)概述
最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来,当测试对象的属性和某个训练对象的属性完全匹配时,便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢,其次就是存在一个测试对象同时与多个训练对象匹配,导致一个训练对象被分到了多个类的问题,基于这些问题呢,就产生了KNN。
KNN是通过测量不同特征值之间的距离进行分类。它的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别,其中K通常是不大于20的整数。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
同时,KNN通过依据k个对象中占优的类别进行决策,而不是单一的对象类别决策。这两点就是KNN算法的优势。
接下来对KNN算法的思想总结一下:就是在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与训练集中对应的特征进行相互比较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类,其算法的描述为:
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
kNN 的基本要素
由上述的流程可知,对于一个确定的训练集,只要确定了距离度量、k值和分类决策规则,就能对任何一个新的实例,确定它的分类。
距离度量
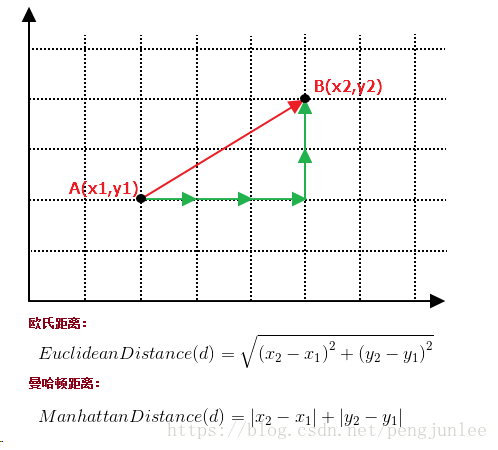
距离就是平面上两个点的直线距离
距离度量是描述特征空间中两个实例的距离,也是这两个实例的相似程度。
关于距离的度量方法,常用的有:欧几里得距离、余弦值(cos), 相关度 (correlation), 曼哈顿距离 (Manhattan distance)或其他。
在 n 维实数向量空间中,我们主要使用的距离度量方式是欧式距离,但也可以使用更加一般的 Minkowski 距离。
Minkowski 距离

欧式距离和曼哈顿距离
from math import * # python3 # 欧式距离 def eculidean_dis(x, y): return sqrt(sum(pow(a - b, 2) for a, b in zip(x, y))) x = [1, 3, 2, 4] y = [2, 5, 3, 1] print(eculidean_dis(x, y)) # 结果为3.872983346207417
# 曼哈顿距离 def manhattan_dis(x, y): return sum(abs(a - b) for a, b in zip(x, y)) print(manhattan_dis(x, y)) # 结果为7
余弦相似度(Cosine Similarity)
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上。

# 余弦相似度 def cosine_dis(x, y): num = sum(map(float, x * y)) denom = np.linalg.norm(x) * np.linalg.norm(y) return round(num / float(denom), 3) x = np.array([3, 4, 1, 5]) y = np.array([3, 4, 1, 5]) print(cosine_dis(x, y)) # 结果为1,这边是相同的两个向量
注:余弦值的范围在[-1,1]之间,值越趋近于1,代表两个向量的方向越接近;越趋近于-1,他们的方向越相反;接近于0,表示两个向量近乎于正交。
KNN中的k值
版权声明:本文为CSDN博主「加油!小小七」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_42234472/article/details/85062142
下面通过一个简单的例子说明一下:如下图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
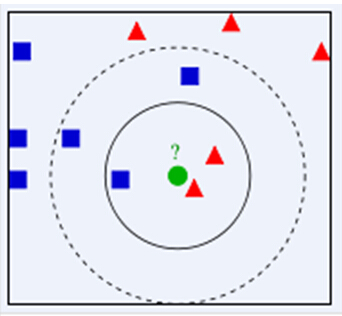
由此也说明了KNN算法的结果很大程度取决于K的选择。
K值如何选择?
答:KNN中的K值选取对K近邻算法的结果会产生重大影响。如李航博士的一书「统计学习方法」上所说:如果选择较小的K值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
如果选择较大的K值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。
K=N,则完全不足取,因为此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的累,模型过于简单,忽略了训练实例中大量有用信息。
在实际应用中,K值一般取一个比较小的数值,例如采用交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)来选择最优的K值。
近似误差和估计误差的关系?
答:近似误差:可以理解为对现有训练集的训练误差。估计误差:可以理解为对测试集的测试误差。
近似误差其实可以理解为模型估计值与实际值之间的差距。 估计误差其实可以理解为模型的估计系数与实际系数之间的差距。
近似误差,更关注于“训练”。估计误差,更关注于“测试”、“泛化”。
最小化近似误差容易过拟合
最小化估计误差整体的泛化能力好。
分类决策规则
kk近邻法中的分类决策规则往往是多数表决,即由输入实例的kk个近邻的训练实例中的多数类决定输入实例的类别。
特征归一化的必要性
首先举例如下,我用一个人身高(cm)与脚码(尺码)大小来作为特征值,类别为男性或者女性。我们现在如果有5个训练样本,分布如下:
A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]
通过上述训练样本,我们看出问题了吗?
很容易看到第一维身高特征是第二维脚码特征的4倍左右,那么在进行距离度量的时候,我们就会偏向于第一维特征。这样造成俩个特征并不是等价重要的,最终可能会导致距离计算错误,从而导致预测错误。口说无凭,举例如下:
现在我来了一个测试样本 F(167,43),让我们来预测他是男性还是女性,我们采取k=3来预测。
下面我们用欧式距离分别算出F离训练样本的欧式距离,然后选取最近的3个,多数类别就是我们最终的结果,计算如下:
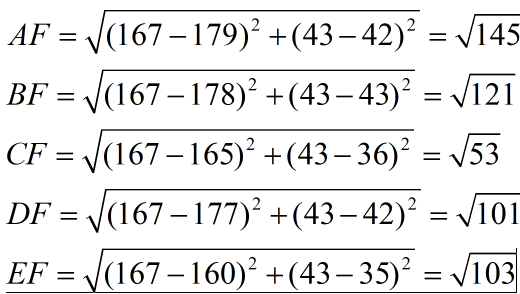
由计算可以得到,最近的前三个分别是C,D,E三个样本,那么由C,E为女性,D为男性,女性多于男性得到我们要预测的结果为女性。
这样问题就来了,一个女性的脚43码的可能性,远远小于男性脚43码的可能性,那么为什么算法还是会预测F为女性呢?那是因为由于各个特征量纲的不同,在这里导致了身高的重要性已经远远大于脚码了,这是不客观的。所以我们应该让每个特征都是同等重要的!这也是我们要归一化的原因!归一化公式如下:

实战
有人曾经统计过很多电影的打斗镜头和接吻镜头,下图显示了 6 部电影的打斗和接吻镜头数。假如有一部未看过的电影,如何确定它是爱情片还是动作片呢?我们可以使用 kNN 来解决这个问题。
构建已经分类好的原始数据集
import pandas as pd import seaborn as sns %matplotlib inline data = {'电影名称':['California Man','He’s Not Really into Dudes','Beautiful Woman','Kevin Longblade','Robo Slayer 3000','Amped II','?'], '打斗镜头':[3,2,1,101,99,98,18], '接吻镜头':[104,100,81,10,5,2,90], '电影类型':['爱情片','爱情片','爱情片','动作片','动作片','动作片','未知']} movie_data = pd.DataFrame(data) movie_data
散点图
sns.lmplot('打斗镜头','接吻镜头',movie_data,hue='电影类型', fit_reg=False)
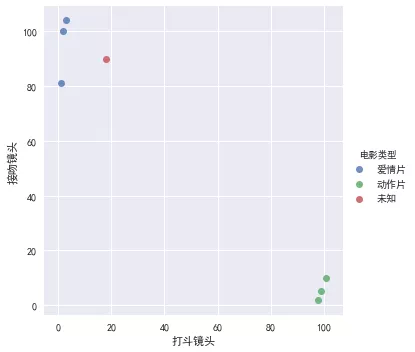
我们可以从散点图中大致推断,这个未知电影有可能是爱情片,因为看起来它距离已知的三个爱情片的点更近一点。那么,具体是如何来度量距离的呢?这个例子中我们使用欧氏距离来衡量。
计算已知类别数据集中的点与当前点之间的距离
new_data=list(movie_data.loc[6][1:3]) dist = list((((movie_data.iloc[:6,1:3]-new_data)**2).sum(1))**0.5) # .iloc:根据标签的所在位置,从 0 开始计数,选取列 # loc:根据 DataFrame 的具体标签选取列 dist
[42.5440947723653, 39.66106403010388, 26.92582403567252, 95.80187889597991, 97.30878685915265, 98.49365461794989]
将距离升序排列,然后选取距离最小的k个点
dist_l = pd.DataFrame({'dist':dist, 'labels':movie_data.iloc[:6,3]})
dr = dist_l.sort_values(by='dist')[:4]
dr
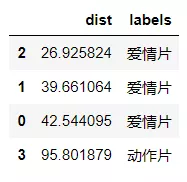
确定前k个点所在类别的出现频率
re = dr.loc[:,'labels'].value_counts() re
爱情片 3 动作片 1 Name: labels, dtype: int64
封装函数
import pandas as pd
def classify0(inX, dataSet, k):
result = []
dist = list((((dataSet.iloc[:,1:3]-inX)**2).sum(1))**0.5)
dist_l = pd.DataFrame({'dist':dist, 'labels':dataSet.iloc[:,3]})
dr = dist_l.sort_values(by='dist')[:k]
re = dr.loc[:,'labels'].value_counts()
result.append(re.index[0])
return result
#classify0(new_data, movie_data[], 4)
sklearn 实现
Scikit-learn 是专门面向机器学习的 Python 开源框架,它实现了各种成熟的算法,并且易于安装与使用。KNeighborsClassifier 在 scikit-learn 在 sklearn.neighbors 包之中。KNeighborsClassifier 使用很简单,三步:
-
创建 KNeighborsClassifier 对象;
-
调用 fit 函数;
-
调用predict函数进行预测。
from sklearn.neighbors import KNeighborsClassifier X = movie_data.iloc[:6,1:3] y = movie_data.iloc[:6,3] neigh=KNeighborsClassifier(n_neighbors=4) neigh.fit(X,y) print(neigh.predict([[18,90]]))
['爱情片']实战
之前,对KNN进行了一个简单的验证,今天我们使用KNN改进约会网站的效果,个人理解,这个问题也可以转化为其它的比如各个网站迎合客户的喜好所作出的推荐之类的,当然,今天的这个例子功能也实在有限。
在这里根据一个人收集的约会数据,根据主要的样本特征以及得到的分类,对一些未知类别的数据进行分类,大致就是这样。
我使用的是python 3.4.3,首先建立一个文件,例如date.py,具体的代码如下:
#coding:utf-8 from numpy import * import operator from collections import Counter import matplotlib import matplotlib.pyplot as plt ###导入特征数据 def file2matrix(filename): fr = open(filename) contain = fr.readlines()###读取文件的所有内容 count = len(contain) returnMat = zeros((count,3)) classLabelVector = [] index = 0 for line in contain: line = line.strip() ###截取所有的回车字符 listFromLine = line.split('\t') returnMat[index,:] = listFromLine[0:3]###选取前三个元素,存储在特征矩阵中 classLabelVector.append(listFromLine[-1])###将列表的最后一列存储到向量classLabelVector中 index += 1 ##将列表的最后一列由字符串转化为数字,便于以后的计算 dictClassLabel = Counter(classLabelVector) classLabel = [] kind = list(dictClassLabel) for item in classLabelVector: if item == kind[0]: item = 1 elif item == kind[1]: item = 2 else: item = 3 classLabel.append(item) return returnMat,classLabel#####将文本中的数据导入到列表 ##绘图(可以直观的表示出各特征对分类结果的影响程度) datingDataMat,datingLabels = file2matrix('D:\python\Mechine learing in Action\KNN\datingTestSet.txt') fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(datingDataMat[:,0],datingDataMat[:,1],15.0*array(datingLabels),15.0*array(datingLabels)) plt.show() ## 归一化数据,保证特征等权重 def autoNorm(dataSet): minVals = dataSet.min(0) maxVals = dataSet.max(0) ranges = maxVals - minVals normDataSet = zeros(shape(dataSet))##建立与dataSet结构一样的矩阵 m = dataSet.shape[0] for i in range(1,m): normDataSet[i,:] = (dataSet[i,:] - minVals) / ranges return normDataSet,ranges,minVals ##KNN算法 def classify(input,dataSet,label,k): dataSize = dataSet.shape[0] ####计算欧式距离 diff = tile(input,(dataSize,1)) - dataSet sqdiff = diff ** 2 squareDist = sum(sqdiff,axis = 1)###行向量分别相加,从而得到新的一个行向量 dist = squareDist ** 0.5 ##对距离进行排序 sortedDistIndex = argsort(dist)##argsort()根据元素的值从大到小对元素进行排序,返回下标 classCount={} for i in range(k): voteLabel = label[sortedDistIndex[i]] ###对选取的K个样本所属的类别个数进行统计 classCount[voteLabel] = classCount.get(voteLabel,0) + 1 ###选取出现的类别次数最多的类别 maxCount = 0 for key,value in classCount.items(): if value > maxCount: maxCount = value classes = key return classes ##测试(选取10%测试) def datingTest(): rate = 0.10 datingDataMat,datingLabels = file2matrix('D:\python\Mechine learing in Action\KNN\datingTestSet.txt') normMat,ranges,minVals = autoNorm(datingDataMat) m = normMat.shape[0] testNum = int(m * rate) errorCount = 0.0 for i in range(1,testNum): classifyResult = classify(normMat[i,:],normMat[testNum:m,:],datingLabels[testNum:m],3) print("分类后的结果为:,", classifyResult) print("原结果为:",datingLabels[i]) if(classifyResult != datingLabels[i]): errorCount += 1.0 print("误分率为:",(errorCount/float(testNum))) ###预测函数 def classifyPerson(): resultList = ['一点也不喜欢','有一丢丢喜欢','灰常喜欢'] percentTats = float(input("玩视频所占的时间比?")) miles = float(input("每年获得的飞行常客里程数?")) iceCream = float(input("每周所消费的冰淇淋公升数?")) datingDataMat,datingLabels = file2matrix('D:\python\Mechine learing in Action\KNN\datingTestSet2.txt') normMat,ranges,minVals = autoNorm(datingDataMat) inArr = array([miles,percentTats,iceCream]) classifierResult = classify((inArr-minVals)/ranges,normMat,datingLabels,3) print("你对这个人的喜欢程度:",resultList[classifierResult - 1])
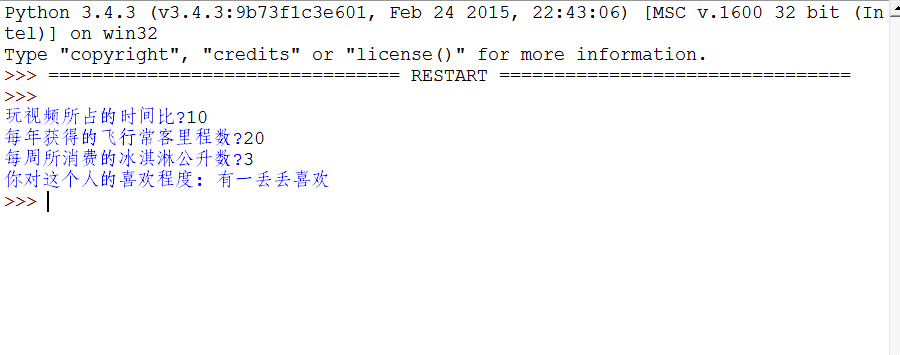
新建test.py文件了解程序的运行结果,代码:
#coding:utf-8 from numpy import * import operator from collections import Counter import matplotlib import matplotlib.pyplot as plt import sys sys.path.append("D:\python\Mechine learing in Action\KNN") import date date.classifyPerson()
运行结果如下图:
以上,是对本次算法的整理和总结。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号