概率论与数理统计

第一章 概率论的基本概念
一、概率的定义和性质
1、定义
满足下列条件的试验称为随机试验:
- 可以在相同的条件下重复地进行;
- 每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果;
- 进行一次试验之前不能确定哪一个结果会出现。
样本点:随机试验的每一个可能结果称为样本点。
样本空间S: 所有样本点全体组成的集合称为样本空间。
随机事件:样本空间S的子集称为随机事件,通常用大写字母A,B,C等表示。
2、事件的关系及运算
事件的关系及运算:(如果理解不了,去搜韦恩图表示)
- A包含B: \(A \supset B\)
- A与B相等: \(A=B\)
- A与B的和: \(A \cup B\)
- A与B的积: \(AB\) 或 \(A \cap B\)
- A与B的差: \(A-B\)
- A与B互斥: \(AB = \emptyset\)
- A的对立事件: \(\bar{A}\)
事件运算的性质:
交换律:
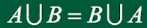
结合律:

分配律:

德摩根律:(长杠变短杠,开口变方向)
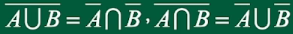
3、概率和频率的定义
频率:在相同条件下,n次试验中,事件A发生的次数,\(n_A / n\) 称为事件A发生的频率
概率:E是随机试验,S是样本空间。对于E的每一事件赋予一个实数,记 \(P(A)\),称为事件A的概率。
二、古典概型和几何概型
1、古典概型
引例:张三李四比赛猜拳,谁先赢10局谁就获得1000元。当比分8:7时,中止比赛,按当前结果如果分配这笔奖金?
解答:按8:7或3:2分配都不合理。比赛最多进行4局分成胜负,按照4局计算所有可能结果,最后结果是11:5

定义:一个试验的样本点有限,并且每个样本点出现的可能性相等,那么这个试验就是古典概型,比如仍骰子。
2、几何概型
定义:如果试验是从某一线段(平面、空间)上取一点,并且所取的点在该线段(平面、空间)内的可能性相同,那么这个试验就是几何概型。
三、条件概率
条件概率\(P(B|A)\)表示已知事件A发生的情况下,事件B发生的概率:
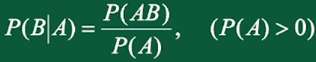
四、全概率公式与贝叶斯公式
韦恩图:B是完备事件组,所有B事件组成样本空间。
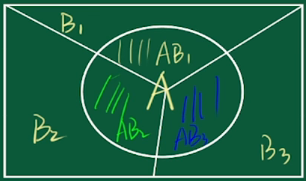
全概率公式用法:有完备事件组(如图中事件B),并且知道事件A与完备事件组B的条件概率,那么就可以求事件A发生的概率。
全概率公式:
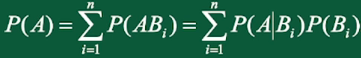
贝叶斯公式用法:有完备事件组(如图中事件B),并且知道事件A与完备事件组B的条件概率,那么就可以求事件B基于事件A的条件概率。
贝叶斯公式:
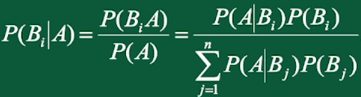
五、事件的独立性
设A,B是两个事件,如果满足:

则称事件A,B相互独立。
第二章 随机变量及其分布
一、定义
1、随机变量
定义:随机变量 \(X\) 是定义在随机试验样本空间 \(S=\{e\}\) 上的单实值函数,记为 \(X=X(e)\)
笔记:随机变量是为了数值化表示,这样更方便数学研究。\(X\) 相当于样本空间,\(x\) 相当于样本点。
2、分布律和概率分布密度
离散型随机变量X的所有可能取值为 \(x_k (k=1,2,3,...)\) ,X取到各个可能值的概率 \(P(X=x_k)=p_k\) ,称为随机变量X的概率论分布,也叫分布律。
举例:骰子每面发生的概率
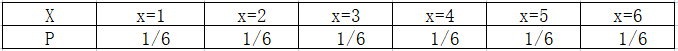
连续型随机变量X在任意位置的概率若为 \(f(x)=P(X=x)\),则称 \(f(x)\) 为随机变量X的概率分布密度。
举例:你7:00-9:00起床的概率
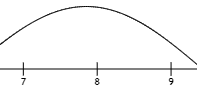
3、分布函数
若 \(F(X) = P(X<=x)\),称随机变量X的分布函数。分布函数表示将随机变量X<=x的所有取值的概率相加。
分布函数和概率密度的关系:
- \(F(x_2) - F(x_1) = \int_{x_1}^{x_2} f(x) dx = P(x_1 <= X <= x_2)\)
- \(F(x) = \int_{-\infty}^{x} f(t) dt\)
笔记:分布函数、概率密度 都是为了更方便研究,从不同角度定义的两个函数。
二、离散型随机变量及其分布
1、0-1分布
随机试验的结果只有两个,随机变量X只有两个可能取值0或1,其分布律可以写成:

也可以写成:
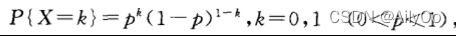
2、二项分布
只有两个结果的随机试验成为伯努利试验,独立重复n次,称为n重伯努利试验。(0-1分布是一次伯努利试验)
假设单独一次试验A发生的概率为p,不发生的概率为q(q=1-p),则n次试验中A发生k次的概率为:

我们把n重伯努利试验中A发生的次数,这个随机变量服从的分布称为二项分布,记 \(B(n,p)\)
3、泊(po)松分布
泊松分布(Poisson distribution)适合于描述单位时间(空间)内随机事件发生的次数。如加油站一个小时内到达的车辆数,一个医院一天内出生的新生儿的数量等等。
泊松分布的分布律:
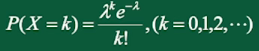
其中 \(\lambda > 0\) 是一个常数,表示单位时间(空间)内随机事件发生的平均次数;k是次数。\(X \sim P(\lambda)\) 表示随机变量X服从参数为 \(\lambda\) 的泊松分布。
泊松定理:
设 \(\lambda > 0\) 是一个常数,n是任意正整数,设 \(np_n = \lambda\),则对于任一固定的非负整数k,有
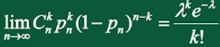
这个定理告诉我们:如果随机变量 \(X \sim B(n, p)\),当n很大,p很小时,X近似服从参数 \(\lambda = np\) 的泊松分布,即
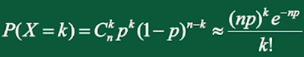
三、连续型随机变量及其概率密度
1、均匀分布
若连续型随机变量X具有概率密度
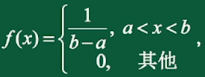
则称随机变量X服从均匀分布,记 \(X \sim U(a, b)\) 。X的分布函数为
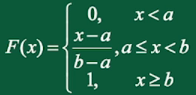
2、指数分布
若连续型随机变量X具有概率密度
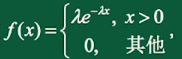
其中 \(\theta > 0\) 为常数,则称X服从指数分布,记 \(X \sim E(\lambda)\) 。 X的分布函数为:

笔记:
- 泊松分布:医院一天内出生新生儿的数量,\(\lambda\)表示一天内平均出生的数量。
- 指数分布:两个新生儿出生的时间间隔,\(\frac{1}{\lambda}\) 表示两个新生儿出生的平均间隔。
3、正态分布
正太分布(Normal distribution),也叫常态分布,高斯分布。
若连续型随机变量X具有概率密度:
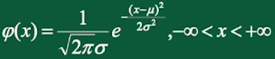
其中 \(\mu ,\sigma\)为常数,则称X服从参数为\(\mu ,\sigma\)的正态分布,记\(X \sim N(\mu, {\sigma}^2)\) 。
若 \(X \sim N(0,1)\) ,称X服从标准正态分布,有概率密度:
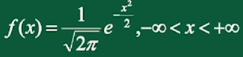
第三章 多维随机变量及其分布
1、二维离散型随机变量
二维离散型随机变量的概率分布(联合分布律):
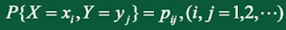
二维离散型随机变量的分布函数:
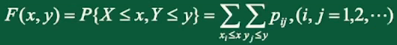
二维离散型随机变量的边缘分布函数:


独立性:
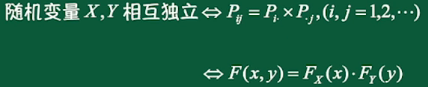
2、二维连续型随机变量
二维连续型随机变量的联合分布函数:
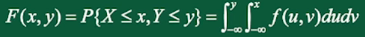
其中,\(f(x,y)\) 是二维连续型随机变量的概率分布函数。
二维连续型随机变量的边缘分布函数:
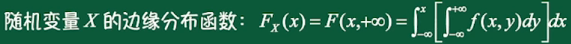
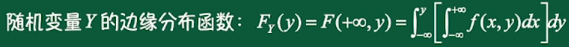
独立性:
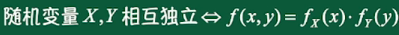
第四章 随机变量的数字特征
1、数学期望
数学期望:随机变量由概率加权的平均值
离散型随机变量的数学期望:
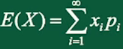
连续型随机变量的数学期望:
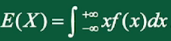
2、方差
方差:偏差平方的概率加权平均值,衡量平均偏离程度(稳定性)
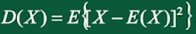
标准差或均方差:

切比雪夫不等式:
设随机变量X,其均值和方差都存在,对任意\(\epsilon > 0\) 均有:
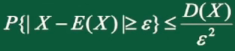
笔记:切比雪夫不等式描述了,在只知道均值和方差的情况下,可以大概知道该点落在某个区间内的概率。
3、协方差及相关系数
协方差:描述二维随机变量X,Y的线性相关性。
设 \((X, Y)\) 是二维随机变量,且EX和EY都存在,X和Y的协方差记作:
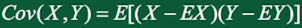
相关系数:由于协方差受量纲(单位)的影响特别严重,如果将每个维度标准化,再计算协方差,通过推理,其结果就是相关系数:
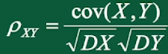
问题1:怎么标准化?
如果这些数据都符合正态分布 \(X \sim N(\mu, {\sigma}^2)\) ,其中均值等于\(\mu\),方差等于\({\sigma}^2\)。标准化过程是:
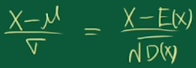
问题2:从协方差到相关系数的推理过程?
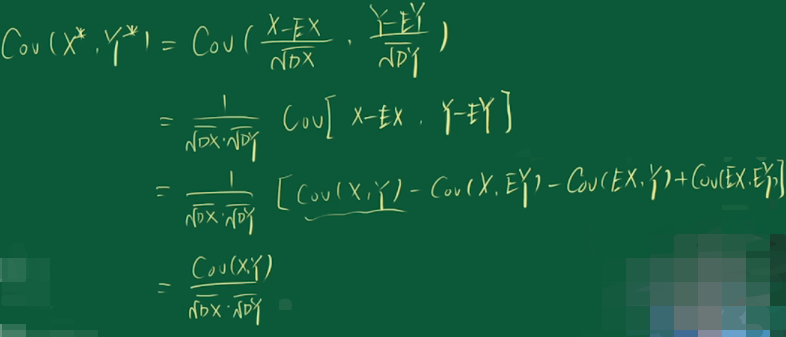
4、矩、协方差矩阵
第五章 大数定律及中心极限定理
一、大数定律
大数定理讲了什么:在样本足够多的情况下,随机变量序列的均值收敛于真实的均值;随机事件发生的概率收敛于真实的概率。
大数定理和中心极限定理为什么有很多条:就像0-1分布和伯努利分布,只有一个统一的定律,其它都是在特殊情况下的变种,这些变种是由不同的人发现的。
辛钦大数定律是切比雪夫大数定律的特殊情况;伯努利大数定律是辛钦大数定律的特殊情况。

二、中心极限定理
中心极限定理讲了什么:无论随机变量服从什么分布,在试验足够多的情况下,它们的算术平均值(如平均身高、平均寿命)都近似服从正态分布。当然,在经过标准化,近似服从标准正态分布。
重点理解:这里不是说X服从正态分布,而是在说 抽样分布 近似服从 正态分布。
什么是抽样分布:如随机抽100人计算平均身高为175,如果再进行类似的9次抽样调查,会得到10组平均身高。根据中心极限定理,这10组抽样的分布服从正态分布,所以我们就不会担心源数据具体是什么分布,都能计算出样本的相关统计量(均值和方差)。
具体数学公式就不列了,就像大数定律,这些公式平常用不到。
数理统计
科学研究有两种逻辑思维方法:
- 演绎法(deduction):从一条公理出发进行推演分析
- 归纳法(induction):从大量经验事实中总结出最接近本质的原理
概率论是演绎法,已知随机变量的分布,去研究问题。
数理统计是归纳法,通过大量试验总结规律。
数理统计的分类:
- 描述统计学:对随机现象进行观测、试验,以取得有代表性的观测值。如抽样方法、试验设计。
- 推断统计学:对已取得的观测值进行整理、分析,作出推断、决策,从而找出所研究的对象的规律性。参数估计、假设检验、方差分析、回归分析。
第六章 样本及抽样分布
一、随机样本
样本基本概念:
- 总体:试验的全部可能观测值,即随机变量X
- 个体:每一个可能的观测值
- 总体容量:总体中包含的个体的数量
- 抽样调查:从总体中随机抽取一部分个体观测结果
- 样本定义:设总体X是具有分布函数F的随机变量,若 \(X_1,X_2,...,X_n\)是与X具有同一分布函数且相互独立的随机变量,则称\(X_1,X_2,...,X_n\)为从总体X得到的容量为n的简单随机样本,简称样本。它们的观测值\(x_1,x_2,...,x_n\)称为样本值。
二、抽样分布
通过样本观察值我们可以获得一些数据,通过对这些数据进行加工处理,可以对总体进行有效的统计推断。这个加工的过程通常就是对样本构造适当的函数。比如我们求样本的平均值,来推断总体的平均值。而这个构造出来的样本的函数我们称为统计量。
统计量是样本的函数,而样本是随机向量,故统计量也是随机变量,统计量的概率分布称为抽样分布。
统计量:样本的函数,不含未知参数。
定义:设\(X_1,X_2,...,X_n\)是来自总体X的一个样本,\(g(X_1,X_2,...,X_n)\)是\(X_1,X_2,...,X_n\)的函数,若g中不含未知的参数,则称\(g(X_1,X_2,...,X_n)\)是一个统计量。
常用的统计量:

三、三大抽样分布
什么是抽样分布:如随机抽100人计算平均身高为175,如果再进行类似的9次抽样调查,会得到10组平均身高。根据中心极限定理,这10组抽样的分布服从正态分布,所以我们就不会担心源数据具体是什么分布,都能计算出样本的相关统计量(均值和方差)。
首先要明确的是,所有分布的前提是所收集的样本要服从正态分布,这需要首先进行正态分布的拟合检验,即使是大样本的情况下,样本正态的情况下分析的结论也会更严谨。
抽样分布可以分为两类:一类是关于均值的分布:正态分布和t-分布;另一类是关于方差的分布:
\(\mathcal{X}\)-分布和F-分布。
1、卡方分布
定义:设 \(X_1,X_2,...,X_n\) 相互独立且均来自总体 \(X \sim N(0,1)\) ,则称统计量
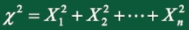
服从自由度为n的 \(\mathcal{X}^2\) 分布,记 \(\mathcal{X}^2 \sim \mathcal{X}^2(n)\)
2、t 分布
为什么叫t分布?因为作者发表文章的笔名叫"Student"
定义:设 \(X \sim N(0,1)\) ,\(Y \sim \mathcal{X}^2(n)\) ,且X,Y相互独立,则称统计量
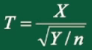
服从自由度为n的 t 分布,记 \(t \sim t(n)\)
3、F 分布
定义:设 \(U \sim \mathcal{X}^2(n_1)\) ,\(V \sim \mathcal{X}^2(n_2)\) ,且U,V相互独立,则统计量
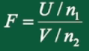
服从自由度为 \((n_1, n_2)\) 的F分布,记 \(F \sim F(n_1, n_2)\)
第七章 参数估计
判断了分布类型后,总体分布中会有一些未知参数,需要用到参数估计的方法:点估计和区间估计。
一、点估计
设总体X的分布函数\(F(x;\theta)\)的形式已知,\(\theta\)是待估计参数。\(X_1,X_2,...,X_n\)是X的一个样本,\(x_1,x_2,...,x_n\)是相应的一个样本值。点估计就是要构造一个适当的统计量\(\hat{\theta}(X_1,X_2,...,X_n)\),用它的观察值\(\hat{\theta}(x_1,x_2,...,x_n)作为未知参数\)\theta$的近似值。我们称
\(\hat{\theta}(X_1,X_2,...,X_n)\) 为 \(\theta\) 的估计量,\(\hat{\theta}(x_1,x_2,...,x_n)\) 为 \(\theta\) 的估计值。
点估计的两种方法:矩估计和最大似然估计。
1、矩估计
用样本矩 估计 总体矩。这里主要是用样本的一阶原点矩(样本均值)来估计总体均值(数学期望)。
2、最大似然估计
最大似然估计的思想是:如果一次试验的结果是A发生了,那么有理由相信A发生的概率就是最大的。因此我们求什么参数取什么值时,这个样本出现的概率最大,就用这个取值作为参数的估计值。
二、区间估计
点估计是对参数估计一个具体的值,而区间估计是对未知参数估计出一个范围。这里主要是对总体的均值和方差进行估计。
主体思想是通过从总体抽取的样本,根据一定的准确度要求,构造出合适的区间,以此作为参数真实值的估计区间。
第八章 假设检验
参考资料
《概率论与数理统计》内容讲解视频
https://www.bilibili.com/video/BV15o4y1R74P?p=22&spm_id_from=pageDriver&vd_source=c680aab5d5ef234c75928d8686b004a5
《概率论与数理统计》知识点总结
https://blog.csdn.net/Aliy66/article/details/123661773




 浙公网安备 33010602011771号
浙公网安备 33010602011771号