刷题日记：递推问题2-力扣.62.不同路径

不久前，咱们幸会了一个递推问题：力扣70.爬楼梯

今天咱们来继续看一道递推问题：力扣.62.不同路径

老规矩，先放出原题：

 

 

 

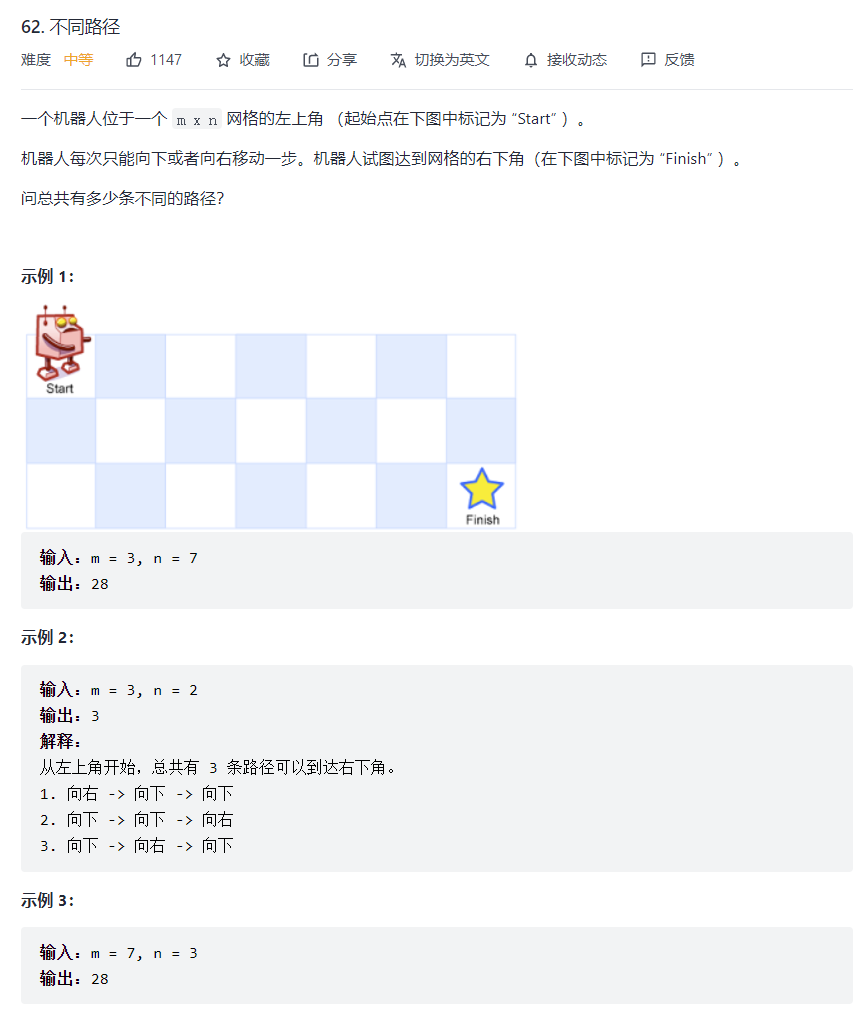
 https://leetcode-cn.com/problems/unique-paths/

 

首先，为啥这是一个递推问题？

因为机器人当前所处的状态都由上一步的状态和行动决定，

同时一次步的状态又由当前状态和行动决定。

 

其次，居然是一个递推问题，咱们上一题讲到最递推问题关键的是啥？

1初始状态，2递归公式。

 

nice，看下初始状态，初始状态是机器人处于左上角。

递推公式呢？由于机器人只能向下向右移动，而咱们要求移动到最后一步的不同路径，

同样采用逆向思维，假设咱们处于最后一格，那它上一个状态是什么呢？只能是处于左边和上边。

咱们用dp[m][n]来表示，通往m（纵坐标），n（横坐标）方格的不同路径，

可以得到如下关系：dp[m][n] = dp[m-1][n] + dp[m][n-1]，

不能说是很像，简直和上一题一模一样，

同时咱们应该看到：一个一维的问题，和一个二维的问题居然会有这么高的相似度。这就是模式的力量。

 OK，这样初始状态和递推公式都有了，咱们就可以开始编码了。

 

老规矩，咱们还是放出了代码的不同版本。

 

这次咱们先看JAVA版：

做个小说明：由于第一列和第一行都只有一个前序位置，所以没办法符合递推公式，因此咱们也给他们做了一个初始化。

其他就按递推公式走。

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i=0; i<m; i++) {
            dp[i][0] = 1;
        }
        for(int j=1; j<n; j++) {
            dp[0][j] = 1;
        }
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

 

 

接着看一下python版：

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0]*n for j in range(m)]

        for i in range(0,m):
            dp[i][0] = 1

        for j in range(1,n):
            dp[0][j] = 1

        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1];

        return dp[m-1][n-1];

 

 

然后是go版本：

func uniquePaths(m int, n int) int {
    var dp[][]int
    dp = make([][]int, m)
    for i := range dp{
        dp[i] = make([]int, n)
    }
    for i:=0; i<m; i++ {
        dp[i][0] = 1;
    }
    for j:=1; j<n; j++ {
        dp[0][j] = 1;
    }
    for i:=1; i<m; i++ {
        for j:=1; j<n; j++ {
             dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

 

 

最后看下C++版：

class Solution {
public:
    int uniquePaths(int m, int n) {
        int dp[m][n];
        for(int i=0; i<m; i++) {
            dp[i][0] = 1;
        }
        for(int j=1; j<n; j++) {
            dp[0][j] = 1;
        }
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

 

 

总结一下，还是和上一篇类似的结论，Go是最节省内存的；python是不太适合for循环的。

 

细心的朋友一定发现了，这次咱们特意把C++放在了最后。原因是我尝试用C++对代码进行了一些优化。

 

也许有人要说，这么简单的代码有什么可优化的？

可千万不能这么想，即便是简简单单的代码，一旦放到生产环境中，可能会被调用千千万万次。

况且咱们学刷算法题，应该追求质量而不是数量，尽量把学习过的东西都吃透才是。

 

那么，这么简单的代码，有什么可以优化的呢？

你想哈，力扣代码排名的指标是啥？是执行时间和内存消耗。

所以呢？优化代码考虑的也是这两点。

 

首先，咱们来考虑一下执行时间，

还是逆着来，咱们要知道一dp[m][n]，就必须知道dp[m][n-1]（前一个）和dp[m-1][n]（上一个）。

咱们要知道dp[m][n-1]，还得知道dp[m][n-2]，，，直到dp[m][1]，

咱们要知道dp[m-1][n]，还得知道dp[m-2][n]，，，直到dp[1][n]，

也就是说，咱们要知道dp[m][n]，就必须把处于它左上的格子的路径都求一遍。

咱们当前的代码，也只是完全循环一遍了这个整列，所以使用递推算法来解这个问题，在循环次数上，咱们已经没有优化空间了。

 

那么空间上呢？

空间上的最大风险在于咱们初始化了dp[m][n]这个数组，根据题意m和n的最大值可以是100，也即100。

如果不局限于这个题的话，数组可能会是一个比较大的值。

 

所以咱们现在来考虑一下，咱们是否真的需要保存这么大的空间。

显然咱们不需要，假设咱们依然按现在的循环方式，目前咱们到了第i行，咱们知道dp[i][0]=1（前一个），所以咱们只需要知道dp[i-1][2]（上一个），就能求出dp[i][2]，

咱们让循环继续进行，同理咱们既然知道了dp[i][2]，那就只需要知道dp[i-1][3]，就能求出dp[i][3]，，，

发现了吗？如果咱们知道上一行的值，就可以递推出这一行的所有值，这样的话咱们只需要2行数组即可，一行用来储蓄咱们需要依赖的值，另一行用来存储咱们正在求得的值。

如下图所示，涂色部分代表了咱们保存的数组，绿色代表咱们需要依赖的值，红色的代表咱们正在计算的值。

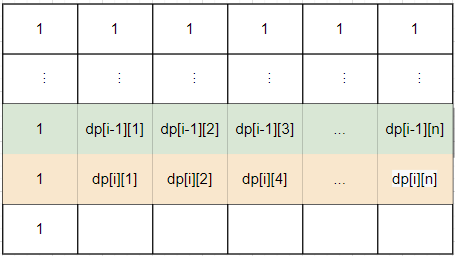
这样是否真的完备了呢？咱们不妨来看下换行的情况，根据上面的推演，已知n行，咱们可以求出i+1行，

而这时候i-1行的内容已经没有作用了，咱们只需要把求得的i+1行的信息存入i-1行即可。

那么咱们把代码改造一下吧：

#include <stdio.h>
class Solution {
public:
    int uniquePaths(int m, int n) {
        int dp[2][n];
        for(int j=0; j<n; j++) {
            dp[0][j] = 1;
        }
        dp[1][0] = 1;
        int i;
        for(i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[i%2][j] = dp[(i-1)%2][j] + dp[i%2][j-1];
            }
        }
        //printf("%d\n",i);
        return dp[(i-1)%2][n-1];
    }
};

这里，在更新数组的时候，咱们使用了一个小小的技巧，咱们把当前值写在了i%2列上，

这样，计算偶数列的时候值会被写在0列，奇数列的值则会被写在1列，免去了咱们手动切换。

怎么样，是否有体会到一点编码的美妙呢？

 

那么这么美妙的代码，效果如何呢？

纳尼！除了击败的人数多了一些，似乎没有任何变化呢，真是遗憾啊！

哦~哦，也许之前是5.89M，现在是5.80也不一定啊！一定是这样的！

 

细心点朋友也许又又发现了，咱们似乎没有必要存储两行数据啊！

还是和刚才一样，绿色是咱们已经求得并保存下来的值，橙色是咱们正在计算的值，

咱们好像只需要把黄色的值覆盖它头上的值就可以了呢？

那么咱们刚才那个小技巧，还可不可以利用呢？

哪里还需要什么小技巧嘛，咱把j列的值写在第j个数组不就好了吗？美妙！

 

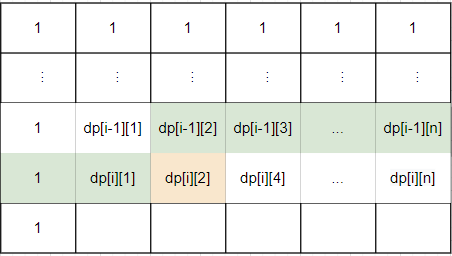
 于是咱们的代码就变成了这样：

class Solution {
public:
    int uniquePaths(int m, int n) {
        int dp[n];
        for(int j=0; j<n; j++) {
            dp[j] = 1;
        }
        int i=1, j = 1;
        for(i=1; i<m; i++){
            for(j=1; j<n; j++){
                dp[j] = dp[j-1] + dp[j];
            }
        }
        return dp[j-1];
    }
};

 

那么把数组长度由2n压榨到n以后的效果又如何呢？

 

 我的天呐，居然战生了99.95的人？

不过你我需要知道，从m*n到2n是一个显著的变化，而2n到n则相对羸弱得多，

所以这个成绩本质上不能说明什么问题，只是运行时波动而已。

如果咱们把2n的代码多运行几次，我敢说一样也会有这样的结果。

 

代码优化到这里其实就差不多了。

但是我发现我被程序员的身份束缚了，如果有人拿这个题去考一个没有学过编程的高中生，

他会不加思索地、充满鄙夷地告诉你，这个是一个简单的排列组合题，学会了只能在高考拿4分。

不妨再来看一下原题的图，咱们要从左上角走到右下角，每次只能向下或向右走一格，

无论咱们怎么走，咱们都需要往下走m-1步，往右走n-1步，总计走m-1 + n-1步。

那个这个问题就变成了从m-1 + n-1步中，选出m-1向下走，剩下的向右走。

也就是C(m+n-2)(m-1)。

那么咱们的代码就变成了：

class Solution {
public:
    int uniquePaths(int m, int n) {

        int p = min(m, n);
        int q = max(m, n);

        long long ans = 1;
        for (int i=1, j=q; i<p; i++, j++) {
            ans = ans * j / i;
        }
        return ans;
    }
};

那么这里咱们又用了什么小技巧呢？咱们知道C(8)(2) = C(8)(6)，为了使循环次数最少，咱们选择计算C(8)(2)。

 

值得一提的是，即便是这种解法，他的内存消耗也并没有什么进步。

 

所以学习算法（我指的是现有的算法）的目的是什么呢？

是用最简单的逻辑，来提升计算机的效率。

你看，使用递推算法，咱们不需要太动脑子，就让效率接近了最佳值。

这世界上所有的发明，都是为了偷懒，算法也是一样！毕竟，思考可是很费头发的。

 

那么今天就酱啦，同样感谢你耐心看完，咱们后会有期。