[寒假家里蹲培训]D1.1基础算法
基础算法
\(\mathbb{A}.\) 枚举
\(\mathfrak{a}\).
一棵苹果树上有\(n\)个苹果,每个苹果长在高度为\(A_i\)的地方。
小明的身高为\(x\)
他想知道他最多能摘到多少苹果
数据范围: \(1 ≤ n,Ai,x ≤ 100\)
基础到不能再基础的题,枚举每个苹果,比较小明身高 Nice~
\(\mathfrak{b}.\)
判断一个数\(X\)是否是素数
\(1 ≤ X ≤ 10^9\)
\(\sqrt n\)枚举判断即可
\(\mathfrak{c}.\)
求\([l,r]\)之间有多少个素数
筛法求素数
\(\mathfrak{d}.\)
T次询问,每次询问\([l,r]\)中有多少素数
筛法筛素数,维护前缀和\(Sum[i]\)记录\([1,i]\)中有多少素数
\(Sum[i]=S[i-1]+if\ \ i\ \ is \ \ prime\)
\(\mathfrak{e}.Luogu\ \ P1036\) 选数
已知n个整数\(x_1, x_2, .., x_n,\)以及一个整数\(k,k < n\)。从\(n\)个数字中任选$k \(个整数相加,可分别得到一系列的和。 例如当\)n = 4, k = 3,$四个整数分别为\(3,7,12,19\)时,可得全部的组合与他们的和为:
\(3 + 7 + 12 = 22\\
3 + 7 + 19 = 29\\
7 + 12 + 19 = 38\\
3 + 12 + 19 = 34\)
现在,要求计算出和为素数的组合共有多少种。
例如上例,只有一种组合的和为素数:\(3 + 7 + 19 = 29\)
\(1 ≤ n ≤ 20, k < n\)
\(1 ≤ x_1, x_2, .., x_n ≤ 5 * 10^6\)
用二进制位表示是否选择第\(i\)个数,不考虑\(k\)的限制,枚举所有状态,然后计算判断是否满足使用\(k\)个数,和是否为质数
for(int i=0;i<1<<n;i++) {
int tmp=0,Sum=0;
for(int j=0;j<n;j++)
if((1<<j)&i) {
tmp++;
Sum+=a[j];
}
if(tmp==k) ans+=Check(Sum);
}
\(Check\)部分即为判断是否为素数。考虑到最大\(Sum\)不超过\(20*500w\),预处理出\(10000\)以内的素数可以加速
\(\mathfrak{f}.\)
求\([l,r]\)中有多少数既是回文数又是素数
\(1\leq l<r\leq 10^7\)
策略\(1\):
枚举每个数,判断他是不是回文数,判断他是不是素数
时间复杂度\(O(N\sqrt N + NlogN)\)
策略\(2\):
预处理出区间所有素数,枚举素数判定是否是回文数
时间复杂度\(O(NlogN)\)
策略\(3\):
枚举区间内所有回文数,判断是否是素数
枚举回文数即枚举一个数的前一半,再手动扩展成完整的数
另外,偶数位数的回文数都必然是11的倍数,不需要枚举。
时间复杂度\(O(\sqrt N *\sqrt N)=O(N)\)
\(\mathfrak{g}.NOIp\)普及组\(2014\ T4\) 子矩阵:
给定一个\(n\)行\(m\)列的矩阵,试找到一个\(r\)行\(c\)列的子矩阵使得这个矩阵里分值最小.
一个矩阵的分值定义为该矩阵中所有相邻元素的差的绝对值之和.
\(1 ≤ n, m ≤ 16\)
由于\(n, m\)的限制,至多只能枚举一边,假设枚举选了哪些行.即先枚举选择了\(r\)行
首先对于每一列,我们可以直接算这一列上的元素的分值.(确定行以后,每一列上下两个格子之间的分值即可算出)
同时对于任意两列,可以算出如果这两列都选,可以得到多少分值.(我们需要对此进行\(dp\),算出选择哪\(c\)列的分值最小)
设\(dp_{i,j}\)表示前\(i\)列中选择了\(j\)列,且最后一列选的是第\(i\)列的最小分值
枚举一个\(k<i,dp_{i,j}=min\{dp_{k,j-1}+costcol_i+cost(i,k)\}\)
其中\(costcol_i\)表示第\(i\)列纵向分值,\(cost(i,k)\)表示第\(i\)列和第\(k\)列横向分值
时间复杂度\(O(C(n,r) * m^2 * n)\),一些有用的信息是\(C(n,r)\)往
往比\(2^n\)小很多.
\(\mathfrak{h}.NOIp\) 普及组\(2016\ T4\) 魔法阵:
有\(m\)个物品,每个物品有一个权值\(X_i,X_i\)不超过\(n\).
现在定义四个构成魔法阵的物品\(a, b, c, d\),满足\(X_a < X_b <X_c < X_d ,X_b − X_a = 2(X_d − X_c )\),且\(X_b − X_a < (X_c − X_b)/3\).
试问每个物品作为\(a, b, c, d\)各出现了多少次?
\(1 ≤ m ≤ 40000, 1 ≤ n ≤ 15000\).
支持常数较小的\(n^2\)算法.
注意到\(n\)比\(m\)小一些,所以肯定是直接枚举物品的大小.
如果直接枚举的话至少需要\(n^3\)的时间.
考虑说枚举\(CD\)之间的长度\(X\),然后从右往左枚举\(D\).
此时\(C\)是固定的,同时我们知道\(B\)要在某个位置的左边.
那么维护\(C\)左边的\((A, B)\)对的个数,在\(D\)往左推的时候,不断去掉不合法的\((A, B)\)对即可

\(\mathbb{B}.\)搜索:
\(\mathfrak{a}.\)
要求输出\(1 ∼ n\)构成的全排列
\(1.next\_permutation\)直接用
\(2.dfs\)
int n,way[N],vis[N];
void dfs(int x) {
if(x==n+1) {
for(int i=1;i<=n;i++)
printf("%d ",way[i]);
puts("");
}
for(int i=1;i<=n;i++) {
if(vis[i]==1) continue;
vis[i]=1;
way[x]=i;
dfs(x+1);
vis[i]=0;
}
}
int main() {
scanf("%d",&n);
dfs(1);
return 0;
}
\(\mathfrak{b}.\)八数码游戏
八数码游戏是一种非常无聊的游戏。给定一个\(3*3\)的格子,在其中\(8\)个格子中放置整数\(1 ∼ 8\),剩下一个格子空着(用\(0\)表示)。每次操作时,你可以选择将某个与空格相邻的数字移动到空格上。给定一个初始局面,求最少需要多少次操作才能将局面变成
\(1\ \ 2 \ \ 3\\
4\ \ 5\ \ 6\\
7\ \ 8 \ \ 0\)
暴力\(BFS\ \ 0\)
多组数据:从最终状态倒着\(BFS\)
\(\mathfrak{c}.\)
给出一个大小为\(N*M\)的迷宫,问从起点到终点最少经过多少障碍物
\(1 ≤ n, m ≤ 1000\)
双端队列,优先扩展没有障碍的
\(\mathfrak{d}.\)
跳房子是大家小时候的体育游戏之一,游戏的规则简单易懂、具有可变性。
我们在地面上画出一个个房子,然后扔石子,根据石子的落地位置确定跳到哪个房子。
我们将房子抽象为\(x\)轴上的连续的正整数坐标点,第\(i\)个房子的坐标为\(i\),并假设房子个数无限。
我们的游戏规则如下:
- 石子落到房子内,记为\(H\),我们可以跳到当前坐标的\(3\)倍坐标位置。
- 石子落到房子外,记为\(O\),我们需跳回当前坐标折半并向下取整的坐标位置。
例如,初始在第\(1\)个房子,要想到达第\(6\)个房子,既可以\(HHHOO\),也可以\(HHOHO\)。
请你编一个程序,给出从第\(n\)个房子到第\(m\)个房子所需要的最少跳跃次数\(k\)和石子的扔法。若最少跳跃次数下存在多种扔法,则选取字典序最小的扔法。
\(1 ≤ N, M ≤ 1000\),数据保证在\(25\)步之内有解。
因为保证在\(25\)步内有解,因此可以\(dfs\),\(dfs\)时遵循先\(H\)后\(O\)的规律
时间复杂度\(O(2^{25})\)
\(\color{Orange}{\mathfrak{e}}.\)
推箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个\(M * N\)的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工只能推箱子而不能拉箱子,因此如果箱子被推到一个角上那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.
现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.
\(N, M ≤ 7.\)
简单的\(BFS\),我们暴力记录人的位置和箱子的位置作为一个\(4\)维的状态,然后进行\(bfs\).
时间复杂度\(O(N * M * N * M)\).
\(\mathbb{C}.\)二分:
\(\mathfrak{a}.\)
一条河上有\(n\)个石子排成一条直线,第\(i\)个石子距离河岸\(x_i\)。
一只年长的青蛙想要从岸边(x=0处)到达第\(n\)个石子上(其实是对岸)。这只青蛙实在是太年长了,所以最多只能跳\(m\)次,而且他希望他这些次跳跃中距离最远的那次距离尽可能的短。请你帮他求出这个最远距离最短能是多少。
\(1 ≤ m ≤ n ≤ 10^5\)
二分最远距离,判断是否合法
\(\mathfrak{b}.\)
给定n个物品,每个物品有属性\(A_i\)和\(B_i\)。
要求在其中选择k个物品,使得选择的物品的\(sum(A)/sum(B)\)尽可能大。
二分答案:
假设\(sum(A_i)/sum(B_i) >= mid\)
则:\(sum(A_i) - mid * sum(B_i) >= 0\)
即:\(sum(A_i-mid*B_i) >= 0\)
将\(Ai-mid*Bi\)作为第\(i\)个物品的权值,问题变为能否选\(k\)个物品使得权值和大于\(0\).此时贪心选择权值最大的\(k\)个物品即可。
\(\mathfrak{c}.\)
给出一个长度为\(n\)的序列\(A_1, A_2, .., A_n\),给出值\(r,k\),定义一个\(sum[i]\)表示区间\([i-r,i+r]\)中\(A_j,j\in [i-r,i+r]\)的和,可以对这个序列进行不超过\(k\)次操作,每次操作选择一个\(A_i\)使其变为\(A_i + 1\)求\(min(sum[i])\) 的最大值
如给出长度为\(5\)的序列\(5\ 4\ 3\ 4\ 9\),给定\(r=0,k=6\)
那么序列可以变为\(6\ 6\ 5 \ 5 \ 9\),得出最优解\(min(sum[i])=5\)
\(1 ≤ r ≤ n ≤ 500000, k ≤ 10^{18}\)
显然\(k\)次都用完最优,考虑二分答案\(mid\),
对一个点判断是否\(\geq mid\),满足无需操作,如果需要增加,则加在区间的末尾
\(\mathfrak{d}.\)三分
初始有一个为空的集合,要求支持两种操作
1.不断向集合中插入一个数,且这个数比集合中所有数都大
2.在集合中找一个子集,使得找到的子集\(S\)中的最大值减去子集\(S\)中元素的平均值的差最大,并输出这个差
操作数\(≤ 500000\)
如何选取子集?
最后插入的这个数是一定要选的,然后再选小的数
就是一个最大数加上几个用来拉低平均值的小数构成了所需子集
小数一定是从最小值开始连续增加使平均值减小,直到达到一个临界点
再增加小数就会使平均值增大,易知这是一个单峰函数
因此考虑三分选多少小数即可
\(\mathbb{D}.\)贪心:
\(OI\)中使用多个错误的贪心策略进行加成有时会有良好的效果
\(\mathfrak{a}.\)
给定\(N\)个农民,第\(i\)个农民有\(A_i\)单位的牛奶,单价\(P_i\)
现在要求从每个农民手中购买不超过\(A_i\)单位,总共\(M\)单位的牛奶。求最小花费
选择价格低的买够\(M\)单位牛奶即可
\(\mathfrak{b}.\)
给定\(n\)个物品,第\(i\)个物品有大小\(l_i\),要求将这些物品装进容积为\(L\)的箱子里,每个箱子至多放两个物品,求最少所需箱子数。
\(1 ≤ n ≤ 10^5\)
将物品从大到小排序
考虑当前的最大物品,假设能与最小值凑成一对,就凑成一对
否则必然不存在一个物品能与他凑成一对,因此单列
用双指针维护这个过程即可
\(\mathfrak{c}.[CF638C]Road \ Improvement\)
给一棵树,定义如果想修理一条边,必须要边的两个点出来维修一天(中途不能够转到别的边上修),问现在想把所有的边都修理了,问如何安排修理才可以让时间最短。
N ≤ 1000000.
1.\(Ans>=max\{度数\}\) 我们可以构造方案使得答案恰好为这个值
2.构造:
从1号点开始,先将所有边都加入不同的集合,然后dfs下去,每次直接放到和父亲边不同的集合里就可以了.

\(\mathfrak{d}.[NOIP2018D1T3]\) 赛道修建
给出一棵带边权的无根树,试找到\(M\)条边不重的路径,使得长度和最短的路径长度尽量长.
\(N ≤ 50000.\)
\(Hint :\)考虑一棵菊花树时的情况
菊花图:
贪心匹配+二分
二分答案最短路径是否\(>=ans\)

\(\mathfrak{e}.\mathcal{YKY}\)打怪
\(YKY\)有\(N\)张卡片,第\(i\)张卡片可以召唤一只攻击力为\(A_i\)的生物,或者让所有生物的攻击力增加\(Bi\).
现在他可以任意调换卡片的顺序,问场攻最高能是多少?
\(N ≤ 100000.\)
枚举选择\(x\)张召唤怪兽,计算\(A_i-B_i*x\),选择代价最小的\(x\)张作为怪兽
三分法\(\color{Red}{????}\)

\(\mathfrak{f}.\)国王游戏:
恰逢\(H\)国国庆,国王邀请n位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 \(n\)位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
\(n ≤ 100000.\)
首先对于一个交换题来说\(i\)和\(i + 1\)交换必不影响其他位置的贡献.
设\(S\)是前面的乘积,\(a_i\)是左手,\(b_i\)是右手.
那么不需要交换等价于\(max(S/b_i, S * a_i/b_{i+1}) < max(S/b_{i+1}, S * a_{i+1}/b_i).\)
乘上\(b_i * b_{i+1}/S\),得到\(max(b_{i+1}, a_i * b_i) < max(b_i, a_{i+1} * b_{i+1}).\)
由于\(b_{i+1}\)必小于\(a_{i+1} * b_{i+1}\),\(a_i * b_i\)大于\(b_i\),要求上式成立,则有\(a_i * b_i < a_{i+1} * b_{i+1}\).
交换还要求比较函数是一个全序,不能A比B好,B比C好,C比A好.
按照\(a_i * b_i\)排序即可.
\(\mathbb{E}.\)分治
\(\mathfrak{a}.\)快速幂
int pow(int x,int k) {
int ans=1;
while(k) {
if(k&1) ans=ans*x%mod;
x=x*x%mod;
k>>=1;
}
return ans;
}
\(\mathfrak{b}.\)归并排序
基本思想:先将整个数组分成两个部分,分别将两个部分排好序,然后将两个排好序的数组\(O(n)\)合并成一个数组。(我懒了)
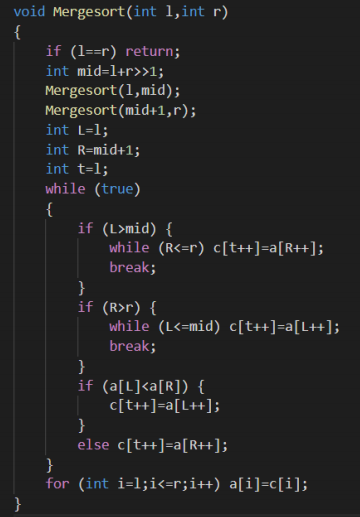
逆序对:
给定一个\(1 ∼ n\)的排列,求逆序对数量。



f[n]为n展开后得到的数字个数:
f[n]=2*f[n/2]+1
查询的时候判断一下是否在查询区间中即可
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<set>
#include<vector>
#include<map>
#include<queue>
#define N 300005
#define M 8000005
#define ls (t<<1)
#define rs ((t<<1)|1)
#define mid ((l+r)>>1)
#define mk make_pair
#define pb push_back
#define fi first
#define se second
using namespace std;
long long i,j,m,n,p,k,ans,l,r;
long long f[105];
long long work(long long x,int dep)
{
if (x<=1) return f[dep]=1;
return f[dep]=2*work(x/2,dep+1)+1;
}
void dfs(long long n,int dep,long long k)
{
if (n<=1) ans+=n;
else if (f[dep+1]+1==k) ans+=n%2;
else if (k<=f[dep+1]) dfs(n/2,dep+1,k);
else dfs(n/2,dep+1,k-f[dep+1]-1);
}
int main()
{
cin>>n>>l>>r;
work(n,0);
for (i=l;i<=r;++i) dfs(n,0,i);
printf("%d\n",ans);
}

给定二维平面上的N个点,求任意两点间的最近距离(欧几里得距离)。
\(1 ≤ n ≤ 10^5\)
不妨按照x坐标排序。对于区间[l,r],我们将其分成mid左右两个部分。
两个点都在左侧:子问题Work(l,mid)
两个点都在右侧:子问题Work(mid+1,r)
两个点一个在左侧,一个在右侧:
重点考虑第三种情况







 浙公网安备 33010602011771号
浙公网安备 33010602011771号