13.1 最小生成树算法

一、普利姆算法(Prim)

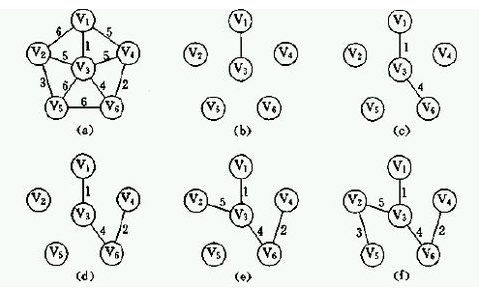
算法思路：以顶点为主导地位，从起始顶点出发，通过选择当前可用的最小权值边把顶点加入到生成树当中来：

　　1.从连通网络N={V,E}中的某一顶点U₀出发，选择与它关联的具有最小权值的边（U₀,V）,将其顶点加入到生成树的顶点集合U中。

　　2.以后每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(U,V),把它的顶点加入到集合U中。如此继续下去，直到网络中的所有顶点都加入到生成树顶点集合U中为止。 

 

二、克鲁斯卡尔算法(kruskal)

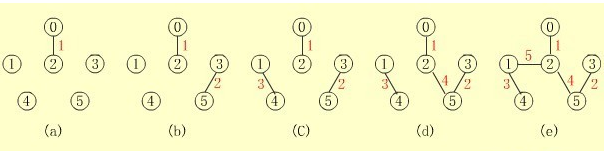
 相比于Prim算法，更常用的还是Kruskal，其原因在于Kruskal算法模板的代码量小而且思路易理解。

　　算法思路：先构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。

　　步骤：

1. 新建图G，G中拥有原图中相同的节点，但没有边；
2. 将原图中所有的边按权值从小到大排序；
3. 从权值最小的边开始，如果这条边连接的两个节点于图G中不在同一个连通分量中，则添加这条边到图G中；
4. 重复3，直至图G中所有的节点都在同一个连通分量中。

　　简单来说就是以边为主导地位，每次选择权值最小的边，判断该边连接的两点是否连通，若不连通，则合并两点（合并操作以并查集实现）。记录合并的次数，当次数等于n-1时结束。

 

三、简单总结

（1）复杂度分析：克鲁斯卡尔算法的时间复杂度为O(eloge)；

         普里姆算法的时间复杂度为，朴素算法O(v^2)，使用小顶堆优化O(VlogV + ElogV)，使用斐波那契堆优化O(E + VlogV)。

（2）克鲁斯卡尔算法主要针对边展开，边数少时效率会很高，所以对于稀疏图有优势而普利姆算法对于稠密图，即边数非常多的情况会好些。

 

四、附加内容

破圈法

每次选定图中一个环，去掉环中最大权值的边，把圈圈破掉。

所有圈破掉时，剩下的就是最小生成树