不同的二叉搜索树

 

 

详细思路

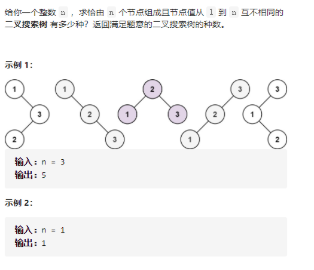
二叉树果断递归，枚举每一个数作为根结点，从左右分别调用dfs得到左右二叉搜索树的分别的个数，答案就是组合就是两边的个数相乘，

 

精确定义

dfs m为二叉搜索树的长度，如果m=1或0返回1，最后返回长度为m的二叉搜索树的个数'

class Solution {
public:
    int numTrees(int n) {
        return dfs(n);
    }
    int dfs(int m){
        if(m==1||m==0)return 1;
        int ans=0;
        for(int i=1;i<=m;i++){
            ans+=dfs(i-1)*dfs(m-i);
        }
        return ans;
    }
};

踩过的坑

 

超时！！！

 

详细思路

因为长度为m的返回值是不会变的，所有递归过程记录返回值

class Solution {
public:
    int numTrees(int n) {
        vector<int>dp(n+1,0);
        dp[1]=1,dp[0]=1;
        return dfs(n,dp);
    }
    int dfs(int m,vector<int>&dp){
        if(dp[m])return dp[m];
        int ans=0;
        for(int i=1;i<=m;i++){
            ans+=dfs(i-1,dp)*dfs(m-i,dp);
        }
        dp[m]=ans;
        return ans;
    }
};

详细思路

记忆化递归可以直接用动态规划，不过几乎一样

class Solution {
public:
    int numTrees(int n) {
        vector<int>dp(n+1,0);
        dp[1]=1,dp[0]=1;
        for(int i=2;i<=n;i++){
            dp[i]+=dp[i-1]*dp[n-i];
        }
        return dp[n];
    }
};