回文自动机（PAM） 学习笔记
原文链接www.cnblogs.com/zhouzhendong/p/PAM.html
前置知识
无。
（强行说和KMP有关也是可以的……）
关于回文串的一些性质
1. 一个长度为 n 的字符串最多有 n 个本质不同的回文子串。
2. 对于一个字符串 S，如果在其之后新插入一个字符，那么最多产生一种新的回文子串。
证明：
假设加入这个字符之后得到的最长回文后缀为 T，那么对于长度小于 T 的任何回文后缀，它们必然在更前面的位置出现过。如图所示：
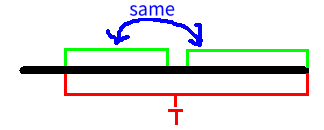
所以只有 T 可能是新的回文子串。
构造PAM
记 len[x] 表示节点 x 代表的回文串长度，设 Fail[x] 表示“代表 节点 x 所代表的回文串的最长回文后缀 的节点”。（注意这里的最长回文后缀是指长度小于原串的最长回文后缀，和后面提到的意义有差别）
设 Next[x][c] 表示节点 x 所代表的字符串在前后都加上一个字符 c 之后所到达的状态。则必然有 len[x] + 2 = len[Next[x][c]] 。
首先，我们建两个节点 A 和 B 。设 len[A] = -1, len[B] = 0 。
于是长度为 1 的回文串就可以有 A 走转移边到达。
接下来考虑如何构建 PAM 。
考虑增量法，在串 s 后面加入一个字符 c 后， PAM 变成了怎样？
假设当前插入的字符是 s[i]，字符串 s 的第 k 个字符为 s[k] 。
设 x 表示 s 的最长回文后缀，那么如果 s[i - len[x] - 1] = s[i] ，那么最长回文后缀就是 Next[x][s[i]]；否则不断使 x = Fail[x] ，直到满足条件就找到了 s 的最长回文后缀。
找到之后，如果 Next[x][s[i]] 这个节点已经存在，那么什么也不用干；否则，我们新建一个节点代表 Next[x][s[i]] ， len[Next[x][s[i]]] = len[x] + 2 ，那么如何求 Fail[Next[x][s[i]]] ？
考虑找到使 x = Fail[x] ，末尾加入字符 s[i] 之后，再找一次最长回文后缀即可。
模板
namespace PAM{
int len[N],Fail[N],Next[N][26];
int cnt;
void init(){
cnt=2;
len[1]=-1,Fail[1]=1;
len[2]=0,Fail[2]=1;
clr(Next);
}
void build(char *s,int n){
init();
s[0]='*';
int x=1;
for (int i=1;i<=n;i++){
while (s[i-len[x]-1]!=s[i])
x=Fail[x];
int c=s[i]-'a';
if (Next[x][c])
x=Next[x][c];
else {
int y=Next[x][c]=++cnt;
len[y]=len[x]+2;
if (len[y]==1)
Fail[y]=2;
else {
x=Fail[x];
while (s[i-len[x]-1]!=s[i])
x=Fail[x];
Fail[y]=Next[x][c];
}
x=y;
}
}
}
}
