BZOJ1040 [ZJOI2008]骑士 基环树林(环套树) 树形动态规划
欢迎访问~原文出处——博客园-zhouzhendong
去博客园看该题解
题意概括
有n个人,每一个人有一个最恨的人。
并且,每一个人有一个权值。
一个人不可以和他最恨的人同时被选中。
现在请你求出在这n个人中选出一些人,使得其权值和最大。
(题解在“心塞史”后面)
心塞史
注:蒟蒻第一次遇见这种基环树题QAQ。
先看样例。
3
10 2
20 3
30 1
Ⅰ
瞬间开心。
随便选了一道,居然是水题?
这种类似的题目我貌似做过,好像是找几个环就可以了?
当然,于是我找完环,打完线性动归,一交wa掉,才发现错了。约2000B。
Ⅱ
然而可怕的事情没这么容易结束。
我灵机一动~哦!不就是环再连一条线出去嘛……
分3种情况dp一下就可以了。
于是又wa掉了。约2500B。
Ⅲ
不过事情总是有转机的。
终于发现这是一道树形dp题,只不过有基环树林(环套树,而且是森林)。
理了2个小时思路,证明了一个连通分量中有且仅有一个环(应该没有自环,一个人总不至于恨自己吧)。
然后开开心心的编。一开始我还以为这一题卡栈空间,为了不用手工扩栈这种卑(ji)鄙(zhi)的手段,我打了bfs序写树形dp。结果有情况没考虑,一发wa掉。3000B
Ⅳ
第二天重看这一题。
之前的代码居然一点都看不懂,于是果断again。最终过了。
题解
这一题是一道基环树林的树形动归题。
我们按照最恨的人建边。
首先,我们可以分析,这个图虽然看似是有向的,实际上是无向的。
那么,两个不同的连通分量是互不影响的。所以我们下面只考虑一个连通分量。对于每一个连通分量,把结果加起来就可以了。
对于一个连通分量,总共有n条边。如果只有n-1条边,那么显然是一棵树。
但是多了一条边,那么这棵树中一定会出现一个环。
有,且仅有一个环!
如果不考虑环,只考虑树,那么我们明显可以写一份树形dp。
用dp[i][0]表示节点i不取的最大权值和,dp[i][1]表示取节点i的最大权值和。
那么设S为节点i的儿子集合,那么,
有dp[i][0] = Σmax(dp[x][0] , dp[x][1]) x∈S
dp[i][1] = Σdp[x][0] x∈S
那么有环的情况怎么办?
其实就是在树形dp的基础上,再限制两个节点不能同时为1。那么实际上我们可以特殊标记。
我们可以先找出环,然后断环,然后分别以环的两个端点为根跑一次树形dp。
但是事情没这么简单。
我们认为不为根的那个端点一定不取,那么我们只要在求完该子树的时候,把它的dp[][0]赋值为-INF即可。
关键是,我们不能随随便便的不取某一个点。
比如说这样一个图:
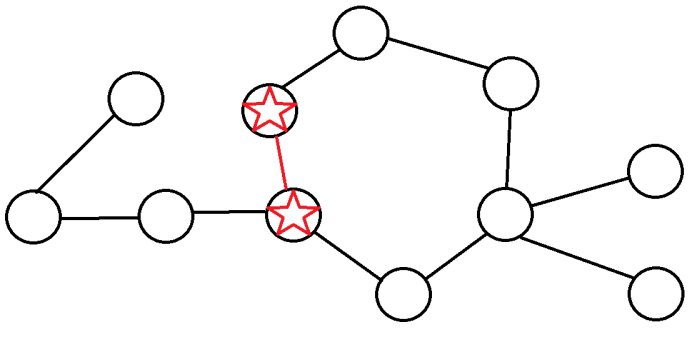
我假设以红色边断开,上面那个节点为根。
我们不可以不访问下面那个。我们要dp。
但是,我们也不能通过两个五角星之间的连边互相访问。
于是我们要判断边。
这里又有一个问题了。
聪(lan)明(duo)的我一开始选择了记录两个端点。
然后莫名wa掉了。
呵呵,对着hzwer大佬的标算对拍了一会儿。排出一组数据。
是这样的:
两个人互相恨对方。任何我保存点的方法就wa掉了。因为他们之间有两条无向边,一条是找环的时候剪掉的,一条其实还是留着的,然而都被我当作没有了。
所以我只能写了记录边的,好像改变不是很大。
我想找个环的事情总不用说了吧?既然你来做这题了,至少应该会找环吧?。
该程序挺繁的,100w个数字,建议读入优化。
代码
#pragma comment(linker, "/STACK:1024000000,1024000000") #include <cstring> #include <algorithm> #include <cstdio> #include <cstdlib> #include <cmath> using namespace std; typedef long long LL; bool isd(char ch){return '0'<=ch&&ch<='9';} void read(int &x) {x=0;char ch=getchar();while (!isd(ch))ch=getchar();while (isd(ch))x=x*10+ch-48,ch=getchar();} void readLL(LL &x){x=0;char ch=getchar();while (!isd(ch))ch=getchar();while (isd(ch))x=x*10+ch-48,ch=getchar();} LL max(LL a,LL b){ return a>b?a:b; } const LL N=1000000+5,M=N*2,INF=N*N; struct Gragh{ int cnt,x[M],y[M],nxt[M],fst[N]; void set(){ cnt=1; memset(fst,0,sizeof fst); } void add(int a,int b){ y[++cnt]=b,x[cnt]=a; nxt[cnt]=fst[a],fst[a]=cnt; } }g; LL v[N],dp[N][2]; int n,p[N],head,tail,fa[N],q[N],vis[N],vis_cnt,dis_use_point; int pointx,pointy,del_point,del_e; void dfs(int prev,int rt){ dp[rt][0]=0,dp[rt][1]=v[rt]; for (int i=g.fst[rt];i;i=g.nxt[i]){ int y=g.y[i]; if (y==prev||i==del_e||(i^1)==del_e) continue; dfs(rt,y); dp[rt][0]+=max(dp[y][0],dp[y][1]); dp[rt][1]+=dp[y][0]; } if (rt==del_point) dp[rt][1]=-INF; } LL solve(int root){ head=tail=0; q[++tail]=root,vis[root]=vis_cnt; fa[root]=0; pointx=pointy=del_point=0; while (head<tail) for (int x=q[++head],i=g.fst[x];i;i=g.nxt[i]){ int y=g.y[i]; if (y==fa[x]) continue; if (vis[y]==vis_cnt){ pointx=x,pointy=y; del_e=i; continue; } vis[y]=vis_cnt; fa[y]=x; q[++tail]=y; } for (int i=1;i<=tail;i++) dp[q[i]][0]=dp[q[i]][1]=0; del_point=pointx; dfs(0,pointy); LL ans1=max(dp[pointy][0],dp[pointy][1]); for (int i=1;i<=tail;i++) dp[q[i]][0]=dp[q[i]][1]=0; del_point=pointy; dfs(0,pointx); LL ans2=max(dp[pointx][0],dp[pointx][1]); return max(ans1,ans2); } int main(){ read(n); for (int i=1;i<=n;i++) readLL(v[i]),read(p[i]); g.set(); for (int i=1;i<=n;i++) g.add(i,p[i]),g.add(p[i],i); memset(vis,0,sizeof vis); vis_cnt=0; LL ans=0; for (int i=1;i<=n;i++){ if (vis[i]) continue; vis_cnt++; ans+=solve(i); } printf("%lld",ans); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号