KSN2021
D1T1
题意
给定一个长度为 \(N\) 字符集为 \(\{{\texttt?},{\texttt A},{\texttt B}\}\) 的字符串,求将每个 \(\texttt?\) 替换为 \(\texttt A\) 或 \(\texttt B\) 后可以得到多少个恰有 \(K\) 个长度为 \(M\) 只包含一种字符的子串。
\(N\leq 3000\)。
题解
考虑 dp。记 \(f_{i,j,c}\) 为长为 \(i\) 的前缀,恰有 \(j\) 个只含一种字符的长为 \(M\) 的子串且结尾字符为 \(c\) 的填法数量。
不难想到枚举结尾的 \(c\) 连续段长度转移。注意到预处理出从每个位置往前可能最长的连续的 \(c\) 的长度后贡献形如矩阵中一列之和与斜对角线之和,可以使用前缀和优化,复杂度 \({\mathcal O}(n^2)\)。
点击查看代码
#include <iostream>
using namespace std;
const int N = 3005, mod = 1e9 + 7;
const char ch[3] = {'A', 'B', '?'};
int n, m, K;
string s;
int las[2];
int f[N][N][2];
int g[N][N][2], h[N][N][2];
int main() {
cin >> n >> m >> K >> s;
f[0][0][0] = f[0][0][1] = 1;
for (int i = 0; i <= n; ++i) g[i][0][0] = g[i][0][1] = h[i][i][0] = h[i][i][1] = 1;
for (int i = 1; i <= n; ++i) {
if (s[i - 1] != '?') las[s[i - 1] - 'A'] = i;
for (int j = 0; j <= K; ++j) {
for (int c = 0; c < 2; ++c) {
int &tmp = f[i][j][c];
if (i - las[!c] >= m) {
tmp = (g[i - 1][j][!c] - g[i - m][j][!c]
+ h[i - m][j - 1][!c] - ((!las[!c] || las[!c] + j - 2 + m < i) ? 0 : h[las[!c] - 1][las[!c] + j - 2 - i + m][!c])) % mod;
} else tmp = g[i - 1][j][!c] - (!las[!c] ? 0 : g[las[!c] - 1][j][!c]);
if (tmp < 0) tmp += mod;
g[i][j][c] = (g[i - 1][j][c] + tmp) % mod;
h[i][j][c] = (h[i - 1][j - 1][c] + tmp) % mod;
}
}
}
cout << (f[n][K][0] + f[n][K][1]) % mod << endl;
return 0;
}
D1T2
题意
\(N\times M\) 的网格图,第 \(i\) 行第 \(j\) 列的格子是黑色当且仅当 \(i\ \text{and}\ j = 0\)。\(Q\) 组询问子矩形内的黑色四连通块数量。
\(N,M\le 10^9,Q\le 10^5\)。
题解
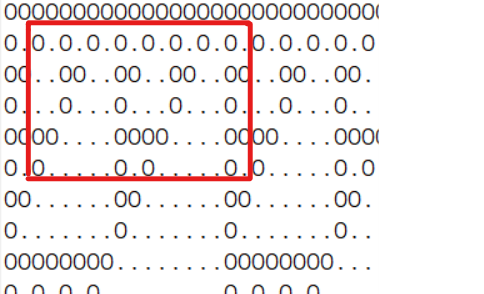
可以看到,放眼于无限大的平面,黑色格子所构成的图形具有以下特点:
- 是一颗树。
- 不存在 \((x,y),(x-1,y),(x,y-1)\) 同为黑色的情况。
有了这两个性质,我们可以断言:红色方框内的连通块数量即为 跨左、上两条边的黑色方格对数。使用数位 dp 求出,复杂度 \({\mathcal O}(Q\log n)\)。
点击查看代码
#include <iostream>
#include <cstring>
using namespace std;
int Q;
int f[40][2];
int dfs(int k, int n, int x, bool op) {
if (k == -1) return 1;
if (f[k][op] != -1) return f[k][op];
if (x >> k & 1) {
if (n >> k & 1) return f[k][op] = dfs(k - 1, n, x, false);
return f[k][op] = dfs(k - 1, n, x, op);
} else {
if (!op) return f[k][op] = dfs(k - 1, n, x, false) * 2;
else if (n >> k & 1) return f[k][op] = dfs(k - 1, n, x, false) + dfs(k - 1, n, x, true);
return f[k][op] = dfs(k - 1, n, x, true);
}
}
int solve(int n, int x) {
if (x == 0 || n == -1) return 0;
memset(f, -1, sizeof f);
return dfs(29, n, x | (x - 1), true);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> Q >> Q >> Q;
while (Q--) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << ((!x1 && !y1) ? 1 : solve(y2, x1) - solve(y1 - 1, x1) + solve(x2, y1) - solve(x1 - 1, y1)) << '\n';
}
return 0;
}
D1T3
题意
\(N\) 个小球排成一行,球有颜色,每次可以向交互库询问区间内颜色数量。需要求出所有小球相对的颜色。记询问上限为 \(Q\)。
\(N\le 1000\)。
- 不超过 \(4\) 种颜色 / 不少于 \(N-1\) 种颜色 / 同种颜色编号连续,\(Q=2000\)。
- 无特殊限制,\(Q=10000\)。
题解
数据分治。
不少于 \(N-1\) 种颜色 / 同种颜色编号连续:思博题。
无特殊限制:从前往后扫,假设进行到第 \(i\) 个球时,已经求出前 \(i-1\) 个球的情况。记 \(f(l,r)\) 为 \([l,r]\) 内颜色数,\(g(x)=[f(x,i-1)=f(x,i)]\)。注意到 \(g\) 取值具有单调性,而 \(f(x,i)\) 可以通过询问交互库得出,二分即可在不超过 \(\log N!\le \frac{1}{2}N\log N\) 次询问解决。
不超过 \(4\) 种颜色:维护每种颜色当前最靠右的位置,并对此二分。精细实现可以使询问数不超过 \(2N\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int Query(int l, int r) {
int x;
cout << "? " << l << ' ' << r << endl;
cin >> x;
return x;
}
int T;
int n, Q;
int col[N], totc = 0;
bool vis[N];
int myque(int l, int r) {
memset(vis, false, sizeof vis);
int cnt = 0;
for (int i = l; i <= r; ++i) if (!vis[col[i]]) vis[col[i]] = 1, ++cnt;
return cnt;
}
int pos[5], tmp[5];
int main() {
cin >> T;
cin >> n >> Q;
if (T == 2) {
col[1] = ++totc;
for (int i = 2; i <= n; ++i) col[i] = Query(i - 1, i) > 1 ? ++totc : col[i - 1];
}
else if (T == 3 || T == 4) {
pos[col[1] = ++totc] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= totc; ++j) tmp[j] = pos[j];
sort(tmp + 1, tmp + totc + 1);
if (totc == 1) col[i] = (Query(1, i) == 1 ? col[1] : ++totc);
else if (totc == 2) col[i] = (Query(tmp[2], i) == 1 ? col[tmp[2]] : Query(tmp[1], i) == 2 ? col[tmp[1]] : ++totc);
else if (totc == 3) col[i] = (Query(tmp[2], i) == 2 ? (Query(tmp[3], i) == 1 ? col[tmp[3]] : col[tmp[2]]) : (Query(tmp[1], i) == 3 ? col[tmp[1]] : ++totc));
else col[i] = (Query(tmp[3], i) == 2 ? Query(tmp[4], i) == 1 ? col[tmp[4]] : col[tmp[3]] : Query(tmp[2], i) == 3 ? col[tmp[2]] : col[tmp[1]]);
pos[col[i]] = i;
}
}
else if (T == 5) {
bool flag = false;
for (int i = 1; i <= n; ++i) {
if (!flag && Query(1, i) < i) {
flag = true;
col[i] = col[1];
for (int j = i - 1; j > 1; --j) {
if (Query(j, i) < i - j + 1) {
col[i] = col[j];
break;
}
}
} else col[i] = ++totc;
}
} else {
for (int i = 1; i <= n; ++i) {
int l = 1, r = i - 1, p = 0;
while (l <= r) {
int mid = (l + r) / 2;
if (Query(mid, i) == myque(mid, i - 1)) l = mid + 1, p = mid;
else r = mid - 1;
}
if (!p) col[i] = ++totc;
else col[i] = col[p];
}
}
cout << "! ";
for (int i = 1; i <= n; ++i)
if (i < n) cout << col[i] << ' ';
else cout << col[i];
cout << endl;
return 0;
}
D2T1
题意
给定长为 \(N\) 的排列,每次操作可以将当前相邻的两数中删去较大者。求经过任意次操作后的序列个数。
\(N\le 3\times 10^5\)。
题解
观察到性质:\((l,r)\) 能被删空意味着 \([l,r]\) 最小值等于 \(\min(a_l,a_r)\)。
令 \(f_i\) 表示以位置 \(i\) 为结尾的序列个数。根据上述性质容易写出转移并优化。具体地,用数据结构(比如 set)对于所有 \(i\) 维护出 \(p<i\) 满足 \(a_p<\min(a_{p+1},…,a_i)\) 的 \(p\) 所构成集合 \({\rm S}_i\),则转移为 \(f_i=\sum_{j=\max \text{S}_i+1}^{i-1}f_j+\sum_{j\in \text{S}_i}f_j\)。复杂度 \({\mathcal O}(n\log n)\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
const int mod = 1e9 + 7;
int n, a[N];
using ii = pair<int, int>;
int dp[N];
int sum[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
set<ii> s;
sum[0] = 1;
for (int i = 1, res = 0; i <= n; ++i) {
ii u;
while (!s.empty()) {
u = (*s.rbegin());
if (u.first > a[i]) {
res = (res - dp[u.second] + mod) % mod;
s.erase(u);
} else break;
}
if (s.empty()) dp[i] = sum[i - 1];
else dp[i] = (res + sum[i - 1] - sum[u.second]) % mod;
if (dp[i] < 0) dp[i] += mod;
sum[i] = (sum[i - 1] + dp[i]) % mod;
s.insert({a[i], i});
res = (res + dp[i]) % mod;
}
int ans = 0;
for (ii u: s) ans = (ans + dp[u.second]) % mod;
cout << ans << endl;
return 0;
}
D2T2
题意
给定长为 \(N\) 的序列 \(A,B\)。以此生成图 \(G\):\(x\) 与 \(y\) 间有边当且仅当 \(A_x\oplus A_y>\max(A_x,A_y)\)。求每个点所属连通块的 \(B\) 值之和。
\(N\le 10^5,A_i<2^{31}\)。
题解
从生成方式入手,不妨设 \(a<b\),则 \(a\oplus b>\max(a,b)\) 等价于 \(b\) 在 \(a\) 的最高位为 \(0\)。
那么将点按 \(A\) 从大到小排序后扫一遍。如果将此前在当前最高位为 \(0\) 的点暴力连边复杂度难以接受,但是注意到最终的连通性必然形如:所有在此位为最高位且之前有点在此位为 \(0\) 的点 和 此位为 \(0\) 且此后有点以此为最高位的点 所构成的集合同属一连通块。记录下每一位的情况即可做到 \({\mathcal O}(n(\log n+\log V))\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 1e5 + 10;
int n;
struct Node {
int id;
int A, B;
} a[N];
bool cmp(Node x, Node y) { return x.A > y.A;}
vector <int> vec[30];
int pos[30];
int fa[N], sz[N];
LL val[N];
int getfa(int x) { return x ^ fa[x] ? fa[x] = getfa(fa[x]) : x;}
void merge(int u, int v) {
u = getfa(u), v = getfa(v);
if (u ^ v) {
if (sz[u] > sz[v]) swap(u, v);
fa[u] = v, sz[v] += sz[u], val[v] += val[u];
}
}
LL ans[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i].A, a[i].id = i;
for (int i = 1; i <= n; ++i) cin >> a[i].B;
sort(a + 1, a + n + 1, cmp);
for (int i = 1; i <= n; ++i) {
if (!a[i].A) break;
fa[i] = i, sz[i] = 1, val[i] = a[i].B;
int p = 31 - __builtin_clz(a[i].A);
if (!vec[p].empty()) pos[p] = i, vec[p].push_back(i);
for (int j = 0; j < 30; ++j) if (!(a[i].A >> j & 1)) vec[j].push_back(i);
}
for (int i = 0; i < 30; ++i) {
for (int j = 1; j < vec[i].size(); ++j) if (vec[i][j] <= pos[i]) merge(vec[i][j], vec[i][j - 1]);
}
for (int i = 1; i <= n; ++i) ans[a[i].id] = val[getfa(i)];
for (int i = 1; i <= n; ++i) cout << ans[i] << endl;
return 0;
}
D2T3
题意
二维平面,第 \(i\) 列有一座高度为 \(H_i\) 的山。你可以进行移动,每次移动可以 左上 / 右上 / 正上,耗费 \(4\) 代价;左下 / 右下 / 正下,耗费 \(1\) 代价;左 / 右,耗费 \(2\) 代价。两个个维度的移动距离均为 \(1\)。可以悬空,不能穿山。
\(Q\) 组询问,每次给定 \(S_i,T_i\),问从 \(S_i\) 列的山峰移动到 \(T_i\) 列的山峰最少需要多少代价。
\(N,Q\le 2\times10^5\)。
题解
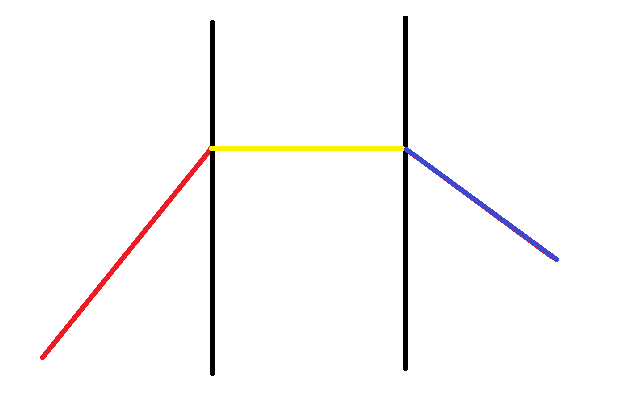
不妨设 \(s<t\),其路线必然形如上图。其中红色的上升段仅有 右 / 正上 / 右上,黄色的平行段仅有 右,蓝色的下降段仅有 右 / 正下 / 右下。分界点即为最大值最靠左和最靠右的位置。
贪心地选择,必然在红色和蓝色段尽量多的选择 右下 和 右上,因为这可以减少总的移动次数。怎样尽量多的选择?以红色段为例,我们考虑在最开始的时候抬升到一个位置,使得其可以持续向右上走直到达到黄色段的高度。如图:
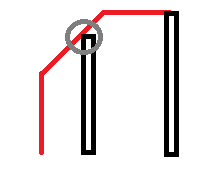
由于不希望浪费步数,最优策略一定会如上图一样,使得这条斜线恰好切到某座山,那么抬升的高度即为 过这些点斜线的截距最大值 - 过起点斜线的截距,也即 \(\left(\max\limits_{i=s}^p(H_i-i)\right)-(H_s-s)\),其中 \(p\) 为分界点位置。仔细思考,由于过分界点后的点斜线的截距一定变小,因此无需知道分界点。直接用 ST 表维护,复杂度 \({\mathcal O}(n\log n+Q)\)。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, Q, h[N];
int st0[N][20], st1[N][20], st2[N][20];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> h[i];
st0[i][0] = h[i], st1[i][0] = h[i] - i, st2[i][0] = h[i] + i;
}
for (int i = 1, h = 1; i <= 18; ++i, h *= 2) {
for (int j = 1; j + h <= n; ++j) {
st0[j][i] = max(st0[j][i - 1], st0[j + h][i - 1]);
st1[j][i] = max(st1[j][i - 1], st1[j + h][i - 1]);
st2[j][i] = max(st2[j][i - 1], st2[j + h][i - 1]);
}
}
cin >> Q;
while (Q--) {
int s, t;
cin >> s >> t;
int l = min(s, t), r = max(s, t), g = log2(r - l + 1);
int a = max(st0[l][g], st0[r - (1 << g) + 1][g]);
int b = max(st1[l][g], st1[r - (1 << g) + 1][g]);
int c = max(st2[l][g], st2[r - (1 << g) + 1][g]);
cout << a - 4LL * h[s] - h[t] + 2LL * (b + c) << '\n';
}
return 0;
}
总结
这套题目都还比较简单,有些题比较清新,有些则比较套路。不过断断续续做了很长时间,由此可以看出我的菜!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号