可持久化权值线段树/主席树
迫于无奈只好提前开坑。
主席树,是动态开点线段树、权值线段树、可持久化等的结合,可用于解决区间第k小问题。
什么是可持久化?意思是可以支持回退,访问之前的历史版本。
可持久化线段树
这里直接放课件吧,图示很清晰。。
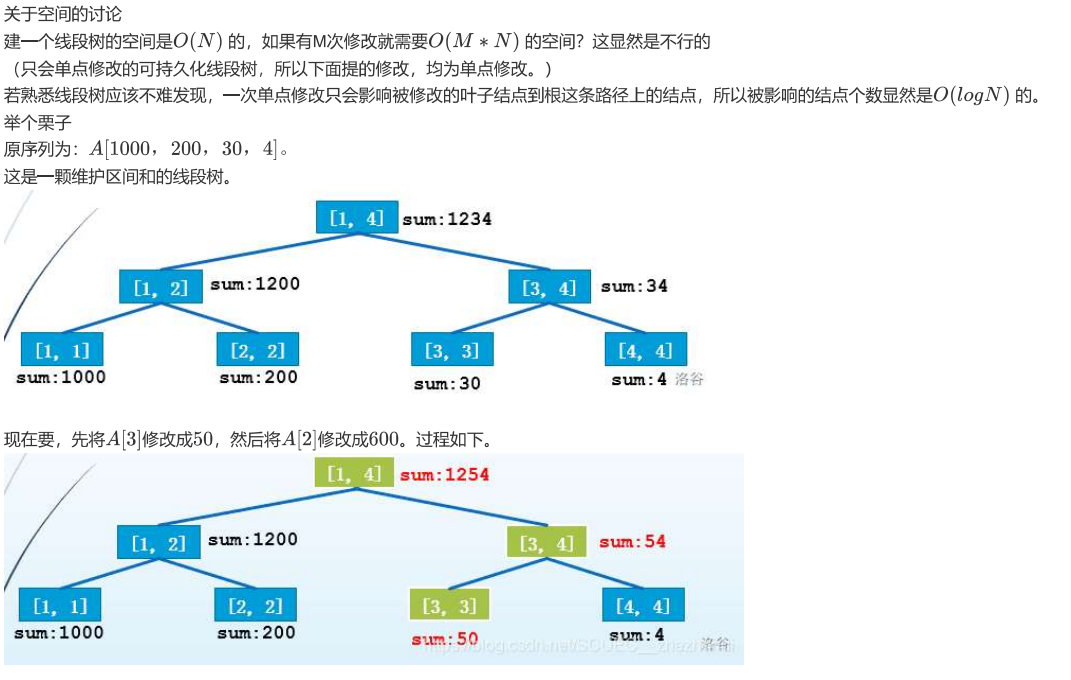
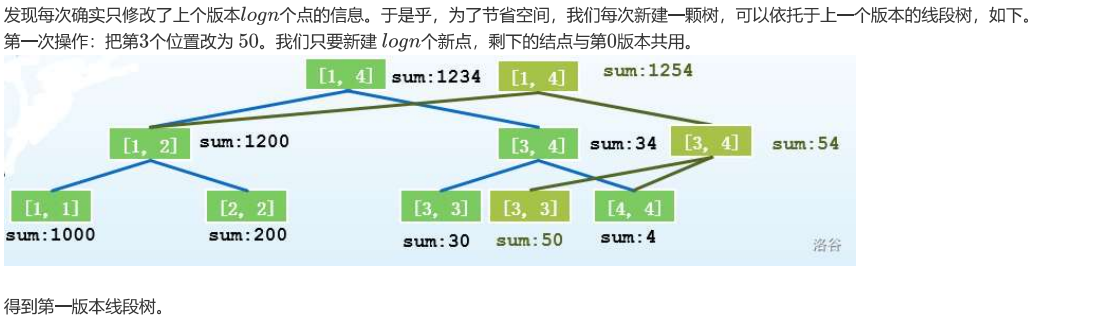
以此类推,把所有点建出来。
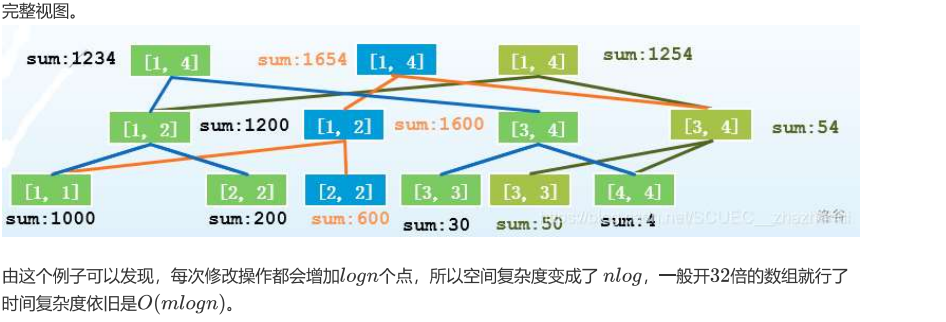
其实最后会发现可持久化线段树就是一堆线段树交错在一起,将没有被修改的儿子重复使用,节省了空间。
主席树的一些性质:
- 每一次修改增加的节点个数为log(n)。
- 增加的非叶子结点会连向一个是其他版本的节点,一个是连向新节点。
- 主席树有很多根。
- 对于每一个根都可以构成一棵完整的线段树。
- 每一个节点都有可能有不只一个爸爸。
例题
例1:【模板】可持久化线段树 1(可持久化数组)
根据题意即可领悟到它和普通动态开点线段树的区别。
然后除了代码实现应该也没啥难理解的。
关于代码实现:虽然有很多节点,但无论它是根还是叶节点,都按照建点顺序编号即可,开一个数组rt记录每个版本的根的序号,线段树tr数组的l和r像动态开点线段树一样记录它的儿子。至于当前节点和历史版本的儿子连边,直接把那个历史版本的 和当前节点同样位置的 节点照搬过来,然后把不一样的地方修改即可。
但其实它的代码也很好写,又短又清晰。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+5;
int n, m, a[maxn], root;
struct tree{
int l, r, val;
}tr[maxn<<5];
int rt[maxn], idx;
int newnode(int id)
{
idx++;
tr[idx]=tr[id];
return idx;
}
void build(int &id,int l,int r)
{
id=++idx;
if(l==r)
{
tr[id].val=a[l];
return ;
}
int mid=(l+r)>>1;
build(tr[id].l, l, mid);
build(tr[id].r, mid+1, r);
}
int update(int id,int l,int r,int p,int val)
{
id=newnode(id);
if(l==r)
{
tr[id].val=val;
return id;
}
int mid=(l+r)>>1;
if(p<=mid) tr[id].l=update(tr[id].l, l, mid, p, val);
else tr[id].r=update(tr[id].r, mid+1, r, p, val);
return id;
}
int query(int id,int l,int r,int p)
{
if(l==r) return tr[id].val;
int mid=(l+r)>>1;
if(p<=mid) return query(tr[id].l, l, mid, p);
else return query(tr[id].r, mid+1, r, p);
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
build(rt[0], 1, n);
for(int i=1;i<=m;i++)
{
int v, opt, p, c;
cin>>v>>opt>>p;
if(opt==1)
{
cin>>c;
rt[i]=update(rt[v], 1, n, p, c);
}
else
{
cout<<query(rt[v], 1, n, p)<<"\n";
rt[i]=rt[v];
}
}
return 0;
}
例2:【模板】可持久化线段树 2
感觉这道更像真正意义上的模板题。
将权值线段树可持久化后就是主席树。
首先可能会有疑惑,题目里没有提到历史版本,那该怎么使用主席树?考虑将序列的1~i看作n个历史版本,修改操作即为每次往里加入一个数,那么查询该怎么办?现在我们所有的历史版本都是[1,i]这个区间的数,考虑类似于前缀和的思想,将第r个版本的线段树“减去”第l-1个版本的线段树。减去这里是指相同位置的节点权值相减。毕竟它的每个节点是对 数的个数 的统计,是有可减性的。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+5;
int n, m, a[maxn], root, lsh[maxn];
struct tree{
int l, r, sum;
}tr[maxn<<5];
int rt[maxn], idx;
int newnode(int id)
{
idx++;
tr[idx]=tr[id];
return idx;
}
void build(int &id,int l,int r)
{
id=++idx;
if(l==r)
{
return ;
}
int mid=(l+r)>>1;
build(tr[id].l, l, mid);
build(tr[id].r, mid+1, r);
}
int update(int id,int l,int r,int p)
{
id=newnode(id);
tr[id].sum++;
if(l==r)
{
return id;
}
int mid=(l+r)>>1;
if(p<=mid) tr[id].l=update(tr[id].l, l, mid, p);
else tr[id].r=update(tr[id].r, mid+1, r, p);
return id;
}
int query(int lx,int rx,int l,int r,int p)
{
int mid=(l+r)>>1;
int sub=tr[tr[rx].l].sum-tr[tr[lx].l].sum;
if(l==r) return l;
if(p<=sub) return query(tr[lx].l, tr[rx].l, l, mid, p);
else return query(tr[lx].r, tr[rx].r, mid+1, r, p-sub);
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
lsh[i]=a[i];
}
sort(lsh+1, lsh+n+1);
int tot=unique(lsh+1, lsh+n+1)-lsh-1;
build(rt[0], 1, tot);
for(int i=1;i<=n;i++)
{
int x=lower_bound(lsh+1, lsh+tot+1, a[i])-lsh;
rt[i]=update(rt[i-1], 1, tot, x);
}
for(int i=1;i<=m;i++)
{
int l, r, k;
cin>>l>>r>>k;
cout<<lsh[query(rt[l-1], rt[r], 1, tot, k)]<<endl;
}
return 0;
}
例3:Count on a tree
延续上一道例题的套路,但现在是在一棵树上,关于树上两点之间的路径,能想到什么?
显然是lca。每一个点成为一个历史版本,那么就把u到v的路径拆分为3条,它是具有可减性的。具体的,就是这么一个式子:
f是倍增父亲数组。剩下的和上一道题一模一样。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+5;
int n, m, idx, tot, a[maxn], lsh[maxn], dep[maxn], f[maxn][20];
int head[maxn], edgenum, rt[maxn];
struct edge{
int next;
int to;
}edge[maxn<<1];
void add(int from,int to)
{
edge[++edgenum].next=head[from];
edge[edgenum].to=to;
head[from]=edgenum;
}
struct tree{
int l, r, sum;
}tr[maxn<<5];
int newnode(int id)
{
idx++;
tr[idx]=tr[id];
return idx;
}
void build(int &id,int l,int r)
{
id=++idx;
if(l==r) return ;
int mid=(l+r)>>1;
build(tr[id].l, l, mid);
build(tr[id].r, mid+1, r);
}
int update(int id,int l,int r,int p)
{
id=newnode(id);
tr[id].sum++;
if(l==r) return id;
int mid=(l+r)>>1;
if(p<=mid) tr[id].l=update(tr[id].l, l, mid, p);
else tr[id].r=update(tr[id].r, mid+1, r, p);
return id;
}
void dfs(int u,int fa)
{
dep[u]=dep[fa]+1;
f[u][0]=fa;
rt[u]=update(rt[fa], 1, n, a[u]);
for(int i=1;i<=18;i++)
{
f[u][i]=f[f[u][i-1]][i-1];
}
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
dfs(v, u);
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x, y);
for(int i=18;i>=0;i--)
{
if(dep[f[x][i]]>=dep[y])
{
x=f[x][i];
}
}
if(x==y) return x;
for(int i=18;i>=0;i--)
{
if(f[x][i]!=f[y][i])
{
x=f[x][i], y=f[y][i];
}
}
return f[x][0];
}
int query(int a,int b,int c,int d,int l,int r,int p)
{
int mid=(l+r)>>1;
int sub=tr[tr[a].l].sum+tr[tr[b].l].sum-tr[tr[c].l].sum-tr[tr[d].l].sum;
if(l==r) return l;
if(p<=sub) return query(tr[a].l, tr[b].l, tr[c].l, tr[d].l, l, mid, p);
else return query(tr[a].r, tr[b].r, tr[c].r, tr[d].r, mid+1, r, p-sub);
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
lsh[i]=a[i];
}
sort(lsh+1, lsh+n+1);
tot=unique(lsh+1, lsh+n+1)-lsh-1;
for(int i=1;i<=n;i++)
{
a[i]=lower_bound(lsh+1, lsh+tot+1, a[i])-lsh;
}
for(int i=1;i<n;i++)
{
int x, y;
cin>>x>>y;
add(x, y), add(y, x);
}
build(rt[0], 1, n);
dfs(1, 0);
int lst=0;
while(m--)
{
int x, y, k;
cin>>x>>y>>k;
x^=lst;
int LCA=lca(x, y);
lst=lsh[query(rt[x], rt[y], rt[LCA], rt[f[LCA][0]], 1, n, k)];
cout<<lst<<endl;
}
return 0;
}
练习
练1:[BZOJ3207]花神的嘲讽计划
因为k是固定的,考虑把一个长为k的子串哈希一下,每一位存从这一位开始k位子串哈希值,然后查询区间中是否存在即可。
☆练2:[HZOI 2015]疯狂的颜色序列
感觉暑假有很多场模拟赛都遇到这种问题然后不会做。。所以给这道题打五角星☆
注意到不同颜色只有在区间内第一次出现才会有贡献,那么就给每个点记录pre表示上一个和它颜色相同的位置,对于区间内的每个点判断pre是否在区间内并累计即可,换言之就是求pre在[1,l]的个数。所以我们反向思考一下,考虑给每个点记录是否成为“上个相同颜色点”,也就是在pre处修改,那么它就具有可减性了,就能判断这一个区间是否改变了它的值,也就是判断是否出现了相同颜色。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号