考试心得4
2025/7/5 | 2025CSP-S模拟赛11
link：https://www.gxyzoj.com/d/hzoj/contest/6864d4194162b00ad15fd4f9/problems
挂着凑数。
2025/7/7 | 2025CSP-S模拟赛12
link：https://www.gxyzoj.com/d/hzoj/contest/68692bd54162b00ad1615dff/problems
明明很颓却不想改变什么，啊。
T1想了1个小时吧，不会写第一个包（据说是搜索？）但我真的没什么头猪，于是写的v=2那个包，其实思路是对的，就把能到达的相邻连续段看成一个点，然后瞎写就可以了，正解是很神仙的状压dp，设pre[s]表示跳的层数的状态为s时最大前缀和，l[i][j]表示在满足第i层限制时，右端点为j的最大连续段的左端点的位置，suf和r数组相反。提前预处理在不同层数时的l和r数组，然后状压转移，最后然后枚举每个子集，看它的补集和它自己能不能构成合法答案即可。
总得来说还是很难的，尤其是打死我也想不到的pre等数组的定义：
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+5;
int n, v, a[maxn], l[20][maxn], r[20][maxn], pre[1<<19], suf[1<<19];
signed main()
{
cin>>n>>v;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
int m=__lg(v)+1;
// cout<<m<<endl;
for(int i=0;i<=m;i++)
{
l[i][1]=1, r[i][n]=n;
for(int j=2;j<=n;j++)
{
if(a[j]-a[j-1]<=(v>>i)) l[i][j]=l[i][j-1];
else l[i][j]=j;
}
for(int j=n-1;j>=1;j--)
{
if(a[j+1]-a[j]<=(v>>i)) r[i][j]=r[i][j+1];
else r[i][j]=j;
}
}
memset(suf, 0x3f3f3f3f, sizeof(suf));
suf[0]=n+1;
for(int i=0;i<=(1<<m)-1;i++)
{
for(int j=1;j<=m;j++)
{
if((i>>(j-1))&1) continue;//第j层是否用过
pre[i|(1<<(j-1))]=max(pre[i|(1<<(j-1))], r[j][min(pre[i]+1, n)]);
suf[i|(1<<(j-1))]=min(suf[i|(1<<(j-1))], l[j][max(suf[i]-1, 1ll)]);
}
}
int cnt=0;
for(int i=1;i<=n;i=r[0][i]+1) cnt++;//第一层连续段数
if(cnt>m+1)
{
for(int i=1;i<=n;i++)
cout<<"Impossible"<<endl;
}
else
{
for(int i=1;i<=n;i=r[0][i]+1)
{
bool flag=0;
for(int j=0;j<=(1<<m)-1&&!flag;j++)
{
if(pre[j]>=i-1&&suf[((1<<m)-1)^j]<=r[0][i]+1) flag=1;
}
for(int j=i;j<=r[0][i];j++)
{
if(flag) cout<<"Possible"<<endl;
else cout<<"Impossible"<<endl;
}
}
}
return 0;
}
T2拼尽全力打暴力，当然正解的二分我也是完全没有想到的。将第n行的数根据二分的答案x，将小于x的设为0，大于等于x的设为1，判断最顶上的数是0还是1即可。有一个很巧妙的性质在于：如果有相邻的两个数相同，那么这两个数上面全都是这个数。然后答案从中间扩展至两边，手模一下即可。
T3其实不难。考试时没有看到这句话“输出点集中的 n 个点或边集中的 n 条边”然后一直在纠结直接输出1不就完了吗。。。其实仔细想想会发现大小为n的独立点集和n条互不有公共顶点的边（即下文中的匹配）加起来刚好有3n个点，也就是说是没有无解的情况的，那么随便搞出来一组匹配，剩余的点就是独立点集啦，肯定满足两个要求中的一个。
T4其实是诈骗题。打表找规律显然，我用一种很感性的方法证明出来（当然也是根据答案推结论）。题解证明：
2025/7/8 | 2025CSP-S模拟赛13
link：https://www.gxyzoj.com/d/hzoj/contest/685aaf3a1d7fa7ec65a04269/problems
拜谢T3数据，大爱评测姬。
T1大概写了1个半小时吧。想到背包dp但设错状态，但是想的有点复杂了，明明是很基础的dp转移。设 \(dp[i][j][k]\) 表示前三个条件分别满足i、j、k个时至少用多少匹马，转移就再枚举xyz三个变量满足不超过ijk并且总花费不超过100，\(dp[i][j][k]=min(dp[i][j][k],dp[i-x][j-y][k-z]+1)\)，你可能会问为啥这里是加1，注意到前面的定义里是“至少”，也就是说完全不考虑前面的马是否有剩余，所以整体还是相对简单的啦。
T2感觉题解写得很复杂啊（？）从部分分理解的话其实很简单：将每个数分解质因数，把立方部分剔除，然后给剩下的数分别配一个数使得他们的乘积为完全立方数，那么这些配的数和原数不能同时出现在选的集合里，答案即为这两种数的个数的最大值。时间复杂度瓶颈在于分解质因数，正解讲得很玄学，但是翻了翻其他大佬的代码例如dzb的：
点击查看代码
il void work(int v) {
ll res1 = 1, res2 = 1;
for(int i = 2; i * i * i <= v; i++) {
int cnt = 0;
while(v % i == 0) v /= i, cnt++;
cnt %= 3;
if(cnt == 1) res1 = res1 * i, res2 = res2 * i * i;
else if(cnt == 2) res1 = res1 * i * i, res2 = res2 * i;
}
int t = sqrt(v);
if(t * t == v) res1 = res1 * v, res2 = res2 * t;
else res1 = res1 * v, res2 = res2 * v * v;
if(res1 == 1) {tot++; return ;}
if(mp.find(res1) == mp.end() && mp.find(res2) == mp.end()) mp[res1] = res2;
num[res1] += 1;
}
2025/7/9 | 2025CSP-S模拟赛14
link：https://www.gxyzoj.com/d/hzoj/contest/6864e3484162b00ad15fdad2/problems
就改了两道题。如何呢？
其实考试时已经做好抱蛋的准备，没想到T1居然还能送50，还是我在1分钟内打的寥寥几行代码取得的。இ௰இ T2的17没拿到不太应该，不就是两遍前缀和吗，我甚至做过类似的题，但考场上却一点都想不到。T3不说了。T4的20分还有提升空间，还有就是有没有人看懂正解20分std是啥意思吗？求解答。
T1是收获最大的啊。考试时打的dfs表示(l,r)区间的最小答案以及剩余魔力值，这就是dp的定义啊！！但因为考场上我深知自己的dp实力于是放弃写区间dp了，dp转移分为两部分：从中间断开左右叠加和前面直接创到后面。剩下的也没啥了。
T2果断跳过。
T3以为又是什么神秘做法。实际上是二分+dp+博弈。注意到子任务二的s和t之间有连边，我们想到此时小N的最优策略一定是尽量走到叶子节点，然后恢复(v,u)这条边再被小Y逼着走到T。基于这样的思路，对于子任务3、4，小N肯定是从s先走一段距离，然后再走到叶子节点最后回退。二分枚举答案，预处理出两个数组：\(f[u]\) 表示从u出发走u的子树最后回到u的最小代价。\(g[u]\) 表示从u点到根节点的所有分叉路经（除了这一条）因为N希望总次数最大所以会选\(f[v]\) 最大的v走，而因为Y他最终只会走次大的。所以\(f[u]= se\max f[v]+son[u]\).check里面如果 \(g[s]+f[v]>mid\) 那么这个v必须删掉，如果有不合法的儿子就剪掉，如果当前操作次数大于可操作次数就返回无解即可。
2025/7/11 | 2025CSP-S模拟赛15
我是鸽子。
果然不能隔太久再写啊，忘得一干二净了
link：https://www.gxyzoj.com/d/hzoj/contest/68686a1d4162b00ad160d895/problems
T1考场上妄图推出正解，，但确实就差一点点，手搓不知道多少组数据，最后发现会根据初始边的两点差和总数n有关联。具体地，设差值为d，那么如果gcd(n,d)
2025/7/12 | 2025CSP-S模拟赛16
我是鸽子*2。
2025/7/14 | 2025CSP-S模拟赛17
不行不能再鸽了啊。。。
link：https://www.gxyzoj.com/d/hzoj/contest/686a3d884162b00ad1617209/problems
T1考场上很显然地看出了是dp，但是根本想不出来，最后打完暴力就跑路（为啥我暴力能打1h？）正解的dp吧，也不是特别难，感觉这个状态设计得是手模样例猜出来的吧。前缀和优化要牢记：dp前先累计，dp转移给下一个状态的l和r。
T2长得挺像钱仓，依然打特殊性质后跑路。尝试写树的包，用的贪心，但还是假掉。自己想的是钱从叶节点和根节点转移出来，实际上从叶节点向上传就可以了，如果儿子的钱大于0但减掉边权后小于0就舍掉，否则会成为累赘。结果判断根节点是否合法即可。转移的过程中无形地将各个点的钱积累在一起，这算dp吗？可能吧。正解就是一棵 \(∑(ai − bi) ≥∑ wi\) 的树一定存在合法方案。与之对立地，如果一棵 \(∑(ai − bi) <∑ wi\) 的树存在合法方案，则必然存在一条边在这个方案中没有被经过，此时删去这条边答案不会变劣。所以对于一个子图，如果它的最小生成树是合法的，那么这个子图就一定是合法的。dp状压转移即可（枚举子集，判断子集和补集是否同时合法即可）。复杂度O(T3^n)。
2025/7/15 | 2025CSP-S模拟赛18
link：https://www.gxyzoj.com/d/hzoj/contest/6864da694162b00ad15fd7e3/problems
险些考好。（＞人＜；）
T1虽然考场上没有推出选的是后缀，但还是大差不差地推完了（其实伪掉），（毕竟我代码里没有对后缀乱七八糟地限制）。首先不难想到排序。考虑选取的一定是一段后缀，证明----假设答案不为后缀，而是由两个区间AB（A左B右）组成的。那么可以把区间A向右平移，直到与B合并更优。于是答案就是最有后缀里答案最大的那一个。
T2是推狮子题。不想写了。
点击查看图片
顺便求问一下：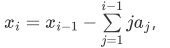
这个式子是怎么得到的？
T3其实不难，第二个包给我们启发了一些思路：对于m中的点，总和即为两两之间的距离*2(m-1)！，那么全排列的问题就解决了。基于这样的思路，考虑统计树上每一条边在m里出现的次数，这个次数怎么计算呢？我们这样考虑一条边，一条边可以把树分为两个部分，那么就是这两个部分的特殊点的个数乘积就是它的值了。那么修改就很方便了。
2025/7/16 | 2025CSP-S模拟赛20
***好烦啊。
link：https://www.gxyzoj.com/d/hzoj/contest/686c954b0b40eb58e00b6adc/problems
T3少打一行初始化痛失80pts。
T1神秘结论题。发现如果下标和其做对应的数的奇偶性不同，那么一定无解。然后注意到一次交换减少了3个逆序对，所以如果总逆序对数不是3的倍数，那也一定无解。再注意到一次交换奇数下标序列或偶数下标序列的逆序对数减一，那么这两种序列的逆序对数是总对数的1/3是有解的必要条件，至于为啥是充分条件。。。
显然这个条件也是充分的。
那我就不说啥了。
T2这个思路真的很巧妙！将时间和位置相互转化了一下，让人难以想到啊，考场上A的都是大佬啊啊Orz
考虑将操作按照位置排序（修改操作差分到两个位置，但最终的修改针对时间的），查询就是查询l到r这段时间值的第k小值。具体来讲，对于一个点x，如果这个点上有修改标记，就把[i,m]这个区间内的时间+k，如果x上有查询标记，就直接查询。因为按照位置排序了，所以无形的根据前面差分修改了当前位置的值，又因为修改的是时间，所以能保证操作不会乱。然后将时间分块以下即可。有个小trick，求l到r的第k小，可以像教主的魔法一样，二分答案，check时判断比该数小的数是否大于等于k即可。
2025/7/19 | 2025CSP-S模拟赛21
link：https://www.gxyzoj.com/d/hzoj/contest/686d04e10b40eb58e00bcdbb/problems
T1的O(nq)太*了，还有我T2T4考场上在干什么啊（6分也是分啊
2025/7/20 | 2025CSP-S模拟赛22
link：https://www.gxyzoj.com/d/hzoj/contest/686f67cc0b40eb58e00d3cbd/problems
T1没开unsigned挂50，哭。没写L=1的，又痛失20pts，那很好了。
考场上妄想O(nlogn）能过，但最后还是我想多了，考虑反着求ST表，原来不是从单个点一步步推向区间的么，现在考虑从区间推向单个点，像这样子：
点击查看代码
for(int j=20;j>=0;j--)
{
for(int i=1;i+(1<<j)<=n;i++)
{
dp[i][j]=max(dp[i][j], dp[i][j+1]);
dp[i+(1<<j)][j]=max(dp[i+(1<<j)][j] , dp[i][j+1]);
}
}
修改的时候直接修改两个长度为2^k的区间即可。
T2线性基？没学过，开学。基向量？阿贝尔群？三维欧氏空间？好，摆烂。few hours later
好像线性基只需要背结论、背代码就好了。首先有个性质就是选原图的任意一棵生成树，那么还会剩下一些环，两点之间的路径异或和可由两点在树上的路径异或上若干个环上的路径所得。树上两点的异或和可以先dfs出来（存为a数组），环上的异或和我们把他们扔到线性基里，那么现在就是要任选两个点 \(a_i a_j\) ，在线性基里选一些异或和（b），使得 \(a_i⊕a_j⊕b\) 最大。令 \(b=b_1\oplus b_2\)，答案即为 \(\max(\max(a_i\oplus b_1) \oplus\min(a_j\oplus b_2))\)，感性理解，我们要尽可能让前者高位含有 1尽可能多，让后者高位含有的 1 尽可能少。求 \(\max(a_i\oplus b_1)\)，直接线性基，若当前异或上 $ d_i $ 更大，就更新；求 $ \min(a_j\oplus b_2)$，就先把 $ a_j$ 翻转，求完最大值然后再翻转回来。
r
然后就是常见的trick：在01trie上解决异或路径最长的问题。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+5;
int n, m, vis[maxn], a[maxn], ans, idx;
int head[maxn], edgenum;
int son[maxn*65][5], cnt[maxn], d[65];
struct edge{
int next;
int to;
int w;
}edge[maxn<<1];
void add(int from,int to,int w)
{
edge[++edgenum].next=head[from];
edge[edgenum].to=to;
edge[edgenum].w=w;
head[from]=edgenum;
}
void add(int x)
{
for(int i=60;i>=0;i--)
{
if(x&(1ll<<i))
{
if(d[i]) x^=d[i];
else
{
d[i]=x;
break;
}
}
}
}
void insert(int x)
{
int p=0;
for(int i=60;i>=0;i--)
{
int u=x>>i&1;
if(!son[p][u]) son[p][u]=++idx;
p=son[p][u];
}
}
void dfs(int u,int fa)
{
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(vis[v])//找到环 扔进线性基
{
add(a[u]^edge[i].w^a[v]);
continue;
}
vis[v]=1;
a[v]=a[u]^edge[i].w;
dfs(v, u);
}
}
int query(int x)//trie树上相反路径
{
int p=0, ans=0;
for(int i=60;i>=0;i--)
{
int u=x>>i&1;
if(son[p][!u]) ans|=1ll<<i, p=son[p][!u];
else p=son[p][u];
}
return ans;
}
int getmax(int x)
{
for(int i=60;i>=0;i--)
{
if((x^d[i])>x) x^=d[i];
}
return x;
}
signed main()
{
// freopen("ex_path2.in","r",stdin);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u, v, w;
cin>>u>>v>>w;
add(u, v, w), add(v, u, w);
}
vis[1]=1;
dfs(1, 0);
for(int i=1;i<=n;i++)
{
insert(getmax(a[i]));//取最大
ans=max(ans, query(~getmax(~a[i])));//取最小
}
cout<<ans;
return 0;
}
/*
5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2
*/
2025/7/21 | 2025CSP-S模拟赛23
link：https://www.gxyzoj.com/d/hzoj/contest/687b61e425f82e94859b0363/problems
又是打部分分的一场。没怎么挂。那很好了。
已经稳定地每天改两道题了。
T1考场上决定先写暴力。事实证明我的选择是正确的，半小时写完40pts然后开始思考正解，当时想到按位考虑了，但是觉得这样不好算平方然后没有继续想下去。其实只要跟紧部分分继续想就行了，手模样例、分类、找规律、猜性质、猜时间复杂度，现在基本都是以这样的策略想T1的。一定不要发呆，没有思路一定要果断跳过。 回到这道题。由异或的性质可得原式变为：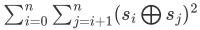
。考虑 \(s_i⊕s_j\) 怎么处理。设 \(s_i=2^a+2^b+2^c\) ，\(s_j=2^b+2^c+2^d\)
那么它们异或后的值即为 \(2^a+2^d\) ，平方后是 \((2^a)^2+2×2^a×2^b+(2^b)^2\)，考虑计算这个值。枚举a和d，记录每个数这两位的情况（计算总个数），只有01 10、10 01、00 11、11 00会有贡献。顺序是无所谓的，所以是01×10+00×11（个数）。a和d都是0~20的范围相当于把×2省略了。再考虑式子两边如何计算。其实枚举的时候已经算过了。即a=d，此时只有00×11，这个就是给a和d不同时的式子补上首项和末项，细想一下会发现个数是一样的。就完啦。
2025/7/22 | 2025CSP-S模拟赛24
link：https://www.gxyzoj.com/d/hzoj/contest/687b9d9025f82e94859b31ab/problems
挂30。其实还好。
T1是不难的构造题。赛时思路没啥问题，写完60pts才意识到距离正解不远了。大样例是在考了一半多才看的，导致自己没有想出数量最多的构造。反正就是很蠢了。考虑每一列按照"ryxy"这样填下去，如果有多余将y所在行按需修改为x，如果不够把最后一行修改为“ryxy”即可。SPJ非常好写。
T2看起来似乎难难哒，实际hh。考虑直接算概率是不简单的，注意到题目里有这样一句话：
，设学生进入实验室的概率为 \(p_i\) ，那么老师抓住学生的期望就是 \((1-p_i)*q_i*a_i\) (设老师进入实验室的概率为 \(q_i\) ，对于题面里的第一句话（同下面的第一/二句话），学生的概率是一定的，那么老师的最优方案一定是让一个q为1，剩下的全为0，那么最优期望是 \(max((1-p_i)*a_i)\) ，因为学生希望这个期望尽量小，考虑二分答案（最大的最小）。因为学生的总概率是1，有第一句话的限制，判定就不难写了。
至于为什么满足第二句话
T3不会改。
T4你猜这个题为啥叫滈葕呢当然最后我写的是dfs的写法。因为CD连边的限制比AB多，所以考虑先放CD，放完了再放AB是比较优的。分三次建图，能填C的（边权为0），能填D的（边权为0，建反图），填AB的（设A为0，B为1，遇到边1就取反，遇到边0就取同）。前两个为什么必须是边权为0的很好理解（只有0才能确保起点和终点都为C/D），建反图是因为D的限制是终点为D的。剩下的代码也不是很难写。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=5e5+5;
int n, m, tot, fl1[maxn], fl[maxn], c[maxn], vis[maxn];
int head[maxn], edgenum;
struct edge{
int next;
int to;
int w;
}edge[maxn<<1];
void add(int from,int to,int w)
{
edge[++edgenum].next=head[from];
edge[edgenum].to=to;
edge[edgenum].w=w;
head[from]=edgenum;
}
struct e{
int u, v, w;
}a[maxn<<1];
int dfs(int u)
{
vis[u]=1;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(vis[v]&&fl[v]==0) continue;
if(fl[v]||dfs(v)==0)
{
fl[u]=1;
return 0;
}
}
c[u]=3;
return 1;
}
int dfs1(int u)
{
vis[u]=1;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(vis[v]&&fl1[v]==0) continue;
if(fl1[v]||dfs1(v)==0)
{
fl1[u]=1;
return 0;
}
}
c[u]=4;
return 1;
}
int dfs2(int u,int col)
{
c[u]=col;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(c[v])
{
if(c[v]!=((c[u]-1)^edge[i].w)+1) return 1;
continue;
}
if(dfs2(v, ((col-1)^edge[i].w)+1)) return 1;
}
return 0;
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int x, y, z;
cin>>x>>y>>z;
if(x==y&&z==1)
{
cout<<"NO";
return 0;
}
if(x!=y)
{
if(z==1) fl1[x]=fl[y]=1;
a[++tot]=(e){x,y,z};
}
}
for(int i=1;i<=tot;i++)
{
if(a[i].w) continue;
if(fl[a[i].u]==0) add(a[i].u, a[i].v, a[i].w);//起点是C的
}
for(int i=1;i<=n;i++)
{
if(!c[i]&&fl[i]==0) dfs(i);
}
memset(head, 0, sizeof(head));
memset(vis, 0, sizeof(vis));
edgenum=0;
memset(edge, 0, sizeof(edge));
for(int i=1;i<=tot;i++)
{
if(a[i].w) continue;
if(fl1[a[i].v]==0) add(a[i].v, a[i].u, a[i].w);//终点是D的
}
for(int i=1;i<=n;i++)
{
if(!c[i]&&fl1[i]==0) dfs1(i);
}
memset(head, 0, sizeof(head));
memset(vis, 0, sizeof(vis));
edgenum=0;
memset(edge, 0, sizeof(edge));
for(int i=1;i<=tot;i++)
{
if(c[a[i].u]||c[a[i].v]) continue;
add(a[i].u, a[i].v, a[i].w);
add(a[i].v, a[i].u, a[i].w);
}
for(int i=1;i<=n;i++)
{
if(!c[i])
{
if(dfs2(i, 1))
{
cout<<"NO"<<endl;
return 0;
}
}
}
cout<<"YES"<<endl;
for(int i=1;i<=n;i++)
{
if(c[i]==1) cout<<"A";
else if(c[i]==2) cout<<"B";
else if(c[i]==3) cout<<"C";
else cout<<"D";
}
return 0;
}
但是这道题不能这么简单地过掉，不能辜负出题人想题目名称的心思。
于是我去学了2-sat。(安利一篇写得特别清楚的博客）对于这道题，设i表示这个点有A凝集素，i+n没有A凝集素，i+2*n有B凝集素，i+3n没有B凝集素。连边时根据题目里的要求和边权的限制连，跑tarjan，缩点，跑拓扑序，根据顺序推出所含有的凝集素分别判断每个点是哪个血型即可。
2025/7/24 | 2025CSP-S模拟赛25
link：https://oj.gxyzh.com/d/hzoj/contest/687ca4e4ff39c5c21831686b/problems
先鸽着。。。
鸽子来补空了！(❁´◡`❁)
今天的T1T2比较简单（既然简单为什么你还没有切），T3个人感觉没有改得很明白，以后有时间再回来看看吧。
T1手模样例即可得出简单的构造，然而自己因为考场上忘记判a-b=3而挂5pts，不说啥了。
T2暴搜就能得95pts，正解是二分+BFS，考场上很容易地3想到了二分，但是自己一直不会写路径的判断（BFS不够熟练啊），然后最后没写。所以在此放一下bfs的代码，一定要熟记！！！
点击查看代码
bool check(int mid)
{
memset(vis, 0, sizeof(vis));
memset(c, 0x3f3f3f3f, sizeof(c));
c[1]=0;
queue<int> q;
while(q.size()) q.pop();
q.push(1);
while(q.size())
{
int u=q.front();
q.pop();
if(vis[u]) continue;
vis[u]=1;
if(u==n) return 1;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if((c[u]+1)*edge[i].w<=mid)
{
c[v]=min(c[v], c[u]+1);//这里就是你想不到的地方
q.push(v);
}
}
}
return 0;
}
2025/7/25 | 2025CSP-S模拟赛26
link：https://oj.gxyzh.com/d/hzoj/contest/687df2ebff39c5c2183230a5/problems
挂了90pts。哭哭哭
由于换了个地方训练导致需要自己带笔记本，打字速度减少了很多，OJ还卡的不行，花了1.5h做T1，1.5h做T2，T3T4几乎没怎么看。最后还是垫底了。
T1该想的性质都想到了，就是没有想到双指针。考场上想k=1那个点时，想偏了然后就没有然后了。后来一看题解恍然大悟，其实每次只需要统计增加了多少个区间，也就是考虑以每个点为右端点的合法区间个数，也就是找到其对应的最小的l，然后这个双指针就很明显了。线段树维护最大子段和一定注意pre，suf的更新 if(tr[lid].maxx==tr[lid].r-tr[lid].l+1) tr[id].pre=tr[lid].maxx+tr[rid].pre;这两行忘写了T1直接爆蛋了🙃
T2的暴力啊，考场上真的写了很久，哪怕是最后20秒我依旧在调，考后加了一行cnt=0直接50了。所以场上的T2我也获得了0pts🙃，好好好，白费3h。
然后正解吧，其实也就多了个预处理和倒着扫一遍。先正着跑一遍，处理出询问为1的答案以及t数组。t数组是干什么的呢？t[i] 表示i这一位数不是最大值的最初时刻，他的作用相当于是对答案的定位，因为我们会发现t值相同的位置答案也是相同的，所以只需要倒着边跑边处理答案并记录即可。
代码实现很巧妙：
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=998244353, maxn=1e6+5;
int n, q[maxn], ans[maxn], lsh[maxn], t[maxn], tot, c[maxn], as[maxn];
struct cz{
int opt, x;
}a[maxn];
int qpow(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
vector<pair<int,int> > vec;
signed main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
int opt, x;
cin>>opt;
a[i].opt=opt;
if(opt==0)
{
cin>>x;
a[i].x=x;
lsh[++tot]=x;
}
}
int cnt=0, sum=0, maxx=0, num=0;
int maxid=0;
for(int i=1;i<=n;i++)
{
if(a[i].opt==0)
{
if(maxx==0)
{
maxx=a[i].x, maxid=i;
}
else if(a[i].x>maxx)
{
sum=(maxx+sum)%mod, maxx=a[i].x;
t[maxid]=i, maxid=i;
cnt++;
}
else
{
sum=(a[i].x+sum)%mod, t[i]=i;
cnt++;
}
}
else
{
if(cnt==0)
{
ans[i]=maxx, ans[maxid]=i, maxx=0;
}
else
{
ans[i]=sum*qpow(cnt, mod-2)%mod;
c[i]=cnt;
sum=(sum-ans[i]+mod)%mod;
cnt--;
}
}
}
for(int i=1;i<=n;i++)
{
if(t[i]) vec.push_back(make_pair(t[i], i));
}
//cout<<endl;
sort(vec.begin(), vec.end());
int anss=0;
int l=vec.size()-1;
for(int i=n;i>=1;i--)
{
if(c[i]) anss=(anss*(c[i]-1)%mod+i)%mod*qpow(c[i], mod-2)%mod;
while(l>=0&&vec[l].first==i)
{
ans[vec[l].second]=anss;
l--;
}
}
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
return 0;
}
Yeah，7/26没有模拟赛。困困地改题。T3是一个输出a[i]之和就能得20pts的题。考场上没想到像区间dp一样设计状态，然后发现很多情况很难处理。设 \(dp[l][r][p]\) 表示第l到第r列只考虑p层（层数自下而上）以上的答案。显然答案是 \(dp[l][r][0]\) 。把所有可能的划分情况归一下类，会发现最终只有两种不同的转移，横着切和竖着切。具体的，前者是将蛋糕从当前l到r中最小的高度横着切，即 \(dp[l][r][p]=dp[l][minid[l][r]-1][a[minid[l][r]]]+dp[minid[l][r]+1][r][a[minid[l][r]]+val\) ，val这个值怎么求就不用细说了。后者就是将蛋糕从最高列两侧切两刀（因为题面里有这样一句话：特别地，对于宽（列数）为
1 的矩形，代价为矩形内权值的最大值。请你最小化划分整个蛋糕的代价。 ），转移就是 \(dp[l][r][p]=dp[l][max[l][r]-1][p]+dp[max[l][r]+1][r][p]+val\) ，然后这两者取min就可以了。
但会发现这个状态个数是n^2的
原因：
2025/7/28 | 2025CSP-S模拟赛28
link：https://oj.gxyzh.com/d/hzoj/contest/687dfcb5ff39c5c218323863/problems
看在后天就可以解放了，这个挂分不提也罢！！
T1鉴于已经多次被创，考场上迅速想到topo排序，也是迅速想出了dp（特别像5.4考的T1的最长路），但是写得时候非常脑抽地写出两个煞笔错误。①dp时没有取max（那这还能叫dp吗）②没有给暂未加入队列的v更新，总结下来和上一场T1犯的错误差不多，就是写得不熟练，然后会因生疏出一些纰漏，警钟长鸣😐
T2过于轻狂认为n小于等于3时只需要判断两点是否相等即可。最后的教训还是要老老实实打爆搜。当然这个题还是特别神奇的。首先将数组差分，即 $ d_i=a_i⊕a_i-1$ ，那么就可以将区间[l,r]修改转化为l和r+1单点修改，显然最终也是希望d数组全为0。考虑将每一个d看作一个点，把一次操作看作两个点之间连一条无向边，那么所有能使得d全为0的操作能将这些点连成若干个联通块，且连通块的边数为x或x-1（x为点数，原因：x-1时即为一棵树，考虑自底向上将底部的数变为0，那么根节点要么为0要么为其他，为0时就不动它了，边数为x-1，否则要增加一条自环的边将根变为0），由此还能得出另一条结论：当该联通块d异或和为0时，操作次数最少为x-1，那么就预处理出d的子序列的异或和是否为0，然后dp枚举子集使得子序列异或和为0的数量最大即可。
T3点分治套点分树，最终硬是看着std把这道题改过去，唉，有点累了，以后再写吧
不行，还是要来写的，从部分分入手，特殊性质A的b相当于没用，问题变成往点集插入一个点，或者询问距离某个点最近的点的距离。
写不完了，颓。
2025/7/29 | 2025CSP-S模拟赛29
link：https://www.gxyzoj.com/d/hzoj/contest/6886df7383c7b5a33cfdcf05/problems
挂19，有进步！
个人认为今天考场上还是尝试了很多以前没有尝试过的东西，比如T1写出来goushi树状数组优化dp，T2写出了点分树（多亏了昨天认认真真改T3）虽然有轻微挂分且依然名次不高但已经很好了，至少我是这么觉得的。
本来想写点废话，还是抓紧正事，先把总结写了吧。
T1想到了以前做的友好城市，然后就完全偏了，虽然也能写，但复杂度最高飙到了O(n2m2)，那直接原地去世（实测其实没炸）所以考场上写了树状数组优化，但因为这个状态本来设得差太多，再怎么优化也是A不了的。其实它本质是个LCS，一般情况下都是dp[i][j]表示第一个串到i，第二个串到j的最大匹配，但显然时空都是过不去的。注意到这个题的答案至多为n，那么我们将答案设到状态里，最后枚举判合法即可。设dp[i][j]表示第一个串到i，答案为j的在第二个串匹配的最小位置。采用刷表法分i+1是否匹配即可，细节不多。
2025/8/9 | 2025CSP-S模拟赛31
link：https://www.gxyzoj.com/d/hzoj/contest/6883500283c7b5a33cfcfc3c/problems
没挂分。
T1打完暴力后干瞪眼了0.5h无果。往最大子矩阵方面想了想也没想出来，原因是一直以为复杂度是O(nm)的。后来听别人一说恍然大悟，n和m里必然有一个小于根号下2e5，复杂度其实是O(n^2m)。两层n分别枚举上下行，m枚举右边的j，维护左边的边的最大值，和后面的三条边拼一起取max。具体一点，可以把这个口字形的框看作两部分：
然后我直接放代码吧，口述真得讲不清楚。。。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n, m, sum[N], cnt, b[N], s1[N], s2[N];
vector<int> vec[N], s[N];
int id(int x,int y)
{
if(x==0||y==0) return 0;
return (x-1)*m+y;
}
signed main()
{
freopen("flower.in","r",stdin);
freopen("flower.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n>>m;
if(n<m)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) cin>>sum[id(i,j)];
}
}
else
{
swap(n,m);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++) cin>>sum[id(j,i)];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
sum[id(i, j)]+=sum[id(i-1, j)]+sum[id(i, j-1)]-sum[id(i-1, j-1)];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
s1[id(i, j)]=sum[id(i, j)]-sum[id(i-1, j-1)];
s2[id(i, j)]=sum[id(i-1, j)]-sum[id(i, j-1)];
}
}
int ans=-1e9;
for(int i=1;i<=n;i++)
{
for(int a=i+1;a<=n;a++)
{
int res=-1e9;
for(int b=1;b<=m;b++)
{
ans=max(ans, res+s1[id(a, b)]-s2[id(i, b)]);
res=max(res, s2[id(a, b)]-s1[id(i, b)]);
}
}
}
cout<<ans;
return 0;
}
/*
5 4
3 -2 -2 -4
0 4 2 1
5 -1 0 -2
-6 -1 1 -1
1 3 -1 0
*/
T2是数据结构优化dp，首先能推出一个简单的dp式子，（然后加一个小优化你就会发现只有一个点T了😐）。
先放一下优化前代码
dp[0]=0;
for(int i=1;i<=n;i++)
{
for(int j=i-1;j>=0;j--)
{
if(sum[i]-sum[j]<=m)
dp[i]=min(dp[i], dp[j]+RMQ(j+1, i));
else break;//小优化
}
}
线段树优化dp的思路是什么呢？线段树维护dp式子里必不可少的部分。考虑每次加入i时，对线段树维护的值的影响，然后进行更改查询。
首先那个sum可以用一个指针l处理出来。注意到影响最小值的有两个东西，dp值和区间最大值，dp这个不用说，肯定是要维护的，设b[k]表示k到i的最大值，考虑每次i++，这个新来的a[i]肯定只会影响[p,i]，其中p是最小的满足b[p]<=a[i]。会发现dp也是单调不减的，那么假如将一个区间[l,r]的b全部修改为val，那它们的答案都为dp[l-1]+val。根据这个修改dp值即可。
优化后
#include<bits/stdc++.h>
#define lid id<<1
#define rid id<<1|1
#define inf 1e18
#define int long long
using namespace std;
const int maxn=1e5+5;
int n, m, a[maxn], dp[maxn], sum[maxn], f[maxn][100], Log2[maxn];
inline void init()
{
for(int i=1;i<=n;i++) f[i][0]=a[i];
for(int j=1;(1<<j)<=n;j++)
{
for(int i=1;i+(1<<j)-1<=n;i++)
{
f[i][j]=max(f[i][j-1], f[i+(1<<j-1)][j-1]);
}
}
}
inline int RMQ(int l,int r)
{
int k=Log2[r-l+1];
return max(f[l][k], f[r-(1<<k)+1][k]);
}
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
x=x*10+ch-'0',ch=getchar();
return x*f;
}
void write(int x)
{
if(x<0)
putchar('-'),x=-x;
if(x>9)
write(x/10);
putchar(x%10+'0');
return;
}
struct seg_tree{
int l, r, b, minn, lazy;
}tr[maxn<<2];
void build(int id,int l,int r)
{
tr[id].l=l, tr[id].r=r;
tr[id].lazy=-1;
if(l==r) return ;
int mid=(l+r)>>1;
build(lid, l, mid);
build(rid, mid+1, r);
}
void pushup(int id)
{
tr[id].minn=min(tr[lid].minn, tr[rid].minn);
tr[id].b=min(tr[lid].b, tr[rid].b);
}
void pushdown(int id)
{
if(tr[id].lazy!=-1)
{
tr[lid].b=tr[id].lazy;
tr[lid].minn=tr[id].lazy+dp[tr[lid].l-1];
tr[rid].b=tr[id].lazy;
tr[rid].minn=tr[id].lazy+dp[tr[rid].l-1];
tr[lid].lazy=tr[id].lazy, tr[rid].lazy=tr[id].lazy;
tr[id].lazy=-1;
}
}
void update(int id,int l,int r,int val)
{
if(tr[id].l>=l&&tr[id].r<=r)
{
tr[id].minn=dp[l-1]+val;
tr[id].lazy=tr[id].b=val;
return ;
}
pushdown(id);
int mid=(tr[id].l+tr[id].r)>>1;
if(l>mid) update(rid, l, r, val);
else if(r<=mid) update(lid, l, r, val);
else update(lid, l, mid, val), update(rid, mid+1, r, val);
pushup(id);
}
int find(int id,int p)
{
if(tr[id].l==tr[id].r) return tr[id].l;
pushdown(id);
int mid=(tr[id].l+tr[id].r)>>1;
if(tr[lid].b<=p) return find(lid, p);
else return find(rid, p);
}
int query(int id,int l,int r)
{
if(tr[id].l>=l&&tr[id].r<=r)
{
return tr[id].minn;
}
pushdown(id);
int mid=(tr[id].l+tr[id].r)>>1;
if(l>mid) return query(rid, l, r);
else if(r<=mid) return query(lid, l, r);
else return min(query(lid, l, mid), query(rid, mid+1, r));
}
signed main()
{
freopen("split.in","r",stdin);
freopen("split.out","w",stdout);
n=read(), m=read();
for(int i=1;i<=n;i++)Log2[i]=(1<<Log2[i-1]+1)>i?Log2[i-1]:Log2[i-1]+1;
for(int i=1;i<=n;i++)
{
a[i]=read();
sum[i]=sum[i-1]+a[i];
}
init();
build(1, 0, n);
memset(dp, 0x3f3f3f3f, sizeof(dp));
dp[0]=0;
int l=1;
for(int i=1;i<=n;i++)
{
while(l<=i&&sum[i]-sum[l-1]>m) l++;
int p=find(1, a[i]);
update(1, p, i, a[i]);
dp[i]=query(1, l, i);
}
cout<<dp[n]<<"\n";
return 0;
}
2025/8/11 | 2025CSP-S模拟赛33
link：https://www.gxyzoj.com/d/hzoj/contest/687e0dcaff39c5c21832557e/problems
又是人均切T1而我没有。原因竟是漏写了一行，大洋里全过了，因为大洋里除了我漏的这一种其他情况都有，惨获90pts高分。然后T2因为该死的重边挂了10分。
T1是很简单的dfs。
T2个人觉得其实不是特别难（那你怎么还不会写）考虑在一棵树且无修改的情况下，答案是 每个点所连的边的颜色个数-1 之和，加上环，如果环上所有颜色相同，那么答案还要+1。然后带上修改
2025/8/14 | 2025CSP-S模拟赛34(nhh)
link：https://www.gxyzoj.com/d/hzoj/contest/6889d7869667b1880c536af9/problems
说实话我其实并没有看懂T1的单调性是为啥。有没有大佬讲一下啊。
T2其实是简单题，最大最小首先能想到二分。二分最终的答案，如果各边总和小于mid的的数的数量不小于k，那么它一定是合法的。（为什么这里是不小于而不是等于呢？因为如果数量大于k，那么有一些数是可以不选的，把多余的剔除掉，此时选的数的答案一定会被二分到），然后显然是要贪心地选数使得数量尽量多，用优先队列实现即可。
点击查看代码
bool check(int mid)
{
priority_queue<int> q;
int sum=0;
for(int i=1;i<=n;i++)
{
q.push(a[i]);
sum+=a[i];
while(sum>mid) sum-=q.top(), q.pop();
b[i]=q.size();
}
sum=0;
while(q.size()) q.pop();
for(int i=n;i>=1;i--)
{
q.push(a[i]);
sum+=a[i];
while(sum>mid) sum-=q.top(), q.pop();
if(b[i-1]+q.size()>=k) return 1;
}
return 0;
}
2025/8/15 | 2025CSP-S模拟赛35
link：https://www.gxyzoj.com/d/hzoj/contest/689731873a834f30a6c2f304/problems
跳跃的时间，是笔者颓废的印记。
算是近几天打得好一点的场了，连续考了3天倒7已经无欲无求了X﹏X
T1赛时以为自己场切了，然而带了一只log遂被卡常（写的还是大常数的线段树）。其实考场上已经想到并查集了，当时写的暴力代码还有一个跳pre的过程，啊啊当时要是多想想就能把并查集写出来了，就是一个求a[i]-1的祖先和把a[i]挂到a[i]-1下两步，真的不难啊。
T2考场上疯狂打表找规律捞到40，事实证明这档部分分对正解几乎没有什么启发。设dp[i][j][0/1][k]表示[1,i-1]和[j+1,n]全部加入，左边大/右边大，大的那边大多少，然后就能推出以下dp式子：
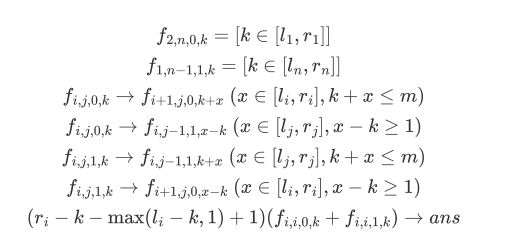
但复杂度显然过不去，考虑差分优化（填表前缀和，刷表差分）。差分的思路就是：找到增加量相同的 只有一维不相同的dp值，将那一维的最小和最大情况差分修改。注意先累加这一维再修改，说得好像有点丑陋，放以下代码（这里只放关键部分，初始化省略）：
优化前
for(int x=l[i];x<=r[i];x++)
{
for(int k=0;k<=m-x;k++) (dp[i+1][j][0][k+x]+=dp[i][j][0][k]%mod)%=mod;
for(int k=0;k<=x-1;k++) (dp[i+1][j][0][x-k]+=dp[i][j][1][k]%mod)%=mod;
}
for(int x=l[j];x<=r[j];x++)
{
for(int k=0;k<=x-1;k++) (dp[i][j-1][1][x-k]+=dp[i][j][0][k]%mod)%=mod;
for(int k=0;k<=m-x;k++) (dp[i][j-1][1][k+x]+=dp[i][j][1][k]%mod)%=mod;
}
优化后（由于我换了写法，暂放了Aapwp_的代码(orz)）
for(int k=m;k>0;k--){
f[i][j][0][k]=(f[i][j][0][k+1]+sum[i][j][0][k])%mod;
f[i][j][1][k]=(f[i][j][1][k+1]+sum[i][j][1][k])%mod;
}
for(int k=0;k<=m;k++){
sum[i+1][j][0][min(k+r[i],m)]=(sum[i+1][j][0][min(k+r[i],m)]+f[i][j][0][k])%mod;
sum[i+1][j][0][min(k+l[i]-1,m)]=(sum[i+1][j][0][min(k+l[i]-1,m)]-f[i][j][0][k]+mod)%mod;
sum[i+1][j][0][max(r[i]-k,0ll)]=(sum[i+1][j][0][max(r[i]-k,0ll)]+f[i][j][1][k])%mod;
sum[i+1][j][0][max(l[i]-k-1,0ll)]=(sum[i+1][j][0][max(l[i]-k-1,0ll)]-f[i][j][1][k]+mod)%mod;
sum[i][j-1][1][max(r[j]-k,0ll)]=(sum[i][j-1][1][max(r[j]-k,0ll)]+f[i][j][0][k])%mod;
sum[i][j-1][1][max(l[j]-k-1,0ll)]=(sum[i][j-1][1][max(l[j]-k-1,0ll)]-f[i][j][0][k]+mod)%mod;
sum[i][j-1][1][min(k+r[j],m)]=(sum[i][j-1][1][min(k+r[j],m)]+f[i][j][1][k])%mod;
sum[i][j-1][1][min(k+l[j]-1,m)]=(sum[i][j-1][1][min(k+l[j]-1,m)]-f[i][j][1][k]+mod)%mod;
}
能很清晰地看出来了吧？注意到上面代码中k的循环起始终止位置不同，但为什么优化后的k可以统一呢？
其实就是把一些条件用min、max来限制，然后还是遵循上面说的差分思想。写的时候一定要一切从简，一些边边角角的地方思考一下，看看能不能把它们归到普通的流程中，不要写太多特判了。
T3改了一上午，是很有必要说一下了，赛时其实已经找到规律，但我自己并没有拆位来算，然后很可惜啊。跟着wyl的做法学的，其实我自己找规律时唯一的问题就是找不到起始位置在哪个循环节里。他这个做法很好的一点就是这一句话：还有更神奇的事情，当 i+1 的贡献循环一次时，i 的贡献加一！就可以通过上一位来定位这一位，然后拆位计算贡献即可。
其实这道题还挺锻炼码力的，自己一开始写了一坨式子竟然一遍过大样例了，写的还是O(n)的做法😁？惨获20pts，然后找啊找啊，在wsq的帮助下，花了2~3小时（包括中间放弃的1h）终于调过了，问题出在这里捏：
- 忘记分讨k的大小，k是否出循环节等等。起始写代码时只需注意(k-a)状物然后用脑子判断一下要不要特判。
- 取模，首先是一些判断类的（如判断k是否出循环节）的数、除数等是不能乱取模的！！只有乘法和加法可以随便取。
然后也没啥了。
2025/8/18 | 2025CSP-S模拟赛36
祝她生日快乐。
T1是小学数学题，考虑只要n大于ax，那么n就减去(ax-b)，否则，答案几位n/x，算出最多能减几个(ax-b)，然后就完了。记得特判特殊情况。
T2其实不是很难，注意到题目里有这样一句话：
保证每种颜色至少出现一次且 n 边形上相邻的两个点颜色不同。
会发现一定没有无解，如果存在一个颜色只出现了一次，那么直接把这个点和所有其他点相连即可。也会发现一定有相邻的3个点颜色互不相同，那么这三个点就可以构成一个三角形，删去中间的点，剩下两个点连边，然后用链表（其实就是开俩数组记录前驱后继）维护没有被删的点。边界条件就是上面那个。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+5;
int n, dp[3005][3005], stk[maxn], top, pre[maxn], nxt[maxn], col[maxn], cnt[5], vis[maxn];
string s;
queue<int> q;
inline bool check(int x)
{
return col[x]!=col[pre[x]]&&col[x]!=col[nxt[x]]&&col[pre[x]]!=col[nxt[x]];
}
vector<pair<int,int> > ans;
int main()
{
freopen("polygon.in","r",stdin);
freopen("polygon.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin>>n>>s;
s=' '+s;
for(int i=1;i<=n;i++)
{
if(s[i]=='R') col[i]=0;
if(s[i]=='G') col[i]=1;
if(s[i]=='B') col[i]=2;
}
for(int i=1;i<=n;i++) cnt[col[i]]++;
for(int i=1;i<=n;i++) nxt[i]=i+1,pre[i]=i-1;
pre[1]=n,nxt[n]=1;
queue<int> q;
for(int i=1;i<=n;i++)
{
if(check(i)) q.push(i);
}
while(1)
{
if(cnt[0]==1||cnt[1]==1||cnt[2]==1)
{
int p=0;
for(int i=1;i<=n;i++)
{
if(!vis[i]&&cnt[col[i]]==1) p=i;
}
for(int i=1;i<=n;i++)
{
if(!vis[i]&&i!=p&&i!=nxt[p]&&i!=pre[p])
ans.push_back(make_pair(p,i));
}
break;
}
int t=q.front();
q.pop();
if(vis[t]) continue;
if(check(t))
{
vis[t]=1;
cnt[col[t]]--;
ans.push_back(make_pair(pre[t],nxt[t]));
pre[nxt[t]]=pre[t];
nxt[pre[t]]=nxt[t];
if(check(pre[t])) q.push(pre[t]);
if(check(nxt[t])) q.push(nxt[t]);
}
}
for(int i=0;i<ans.size();i++) cout<<ans[i].first<<" "<<ans[i].second<<"\n";
return 0;
}
2025/8/19 | 2025CSP-S模拟赛37
link：https://www.gxyzoj.com/d/hzoj/contest/689c4a6f4bf262c31f87f2f0/problems
T2也是签到题。可惜没有看出来，然后就凉了。
T1做了1h都要放弃了，然后开T2的时候突然有了思路，发现自己比较sb地卡在一个点上好久，万幸最后做出来了。
然后T2就想了20多分钟，抱着“自己从没有做出过博弈论题”的心态就去看T3了。
T2没有看清数据范围就去打dp了，然后我打的复杂度疑似是O(n^3)的，而且还开了三个5000*5000数组，还RE了，把我那个前k个s[i]是0的4个点也拖下水了。喜提零蛋🙃
T4也是毫无希望。
写一下T2T3吧，T2当时注意到只需要把点移到一个距离直径端点为1的地方就必胜了，但因为它是一棵树很不好考虑。所以换一种思路，每次把直径两头的点去掉，它的必胜策略和去之前是一样的。去到底只会剩两个或一个节点，那么就能轻而易举地判断出是A还是B赢。总的来说，如果起始点位于直径中点，那么B赢，反之A赢。
2025/8/20 | 2025CSP-S模拟赛38
link：https://www.gxyzoj.com/d/hzoj/contest/689e9d4db330a4c3c5799897/problems
做前3题时心都凉了，看到T4的板子又诈醒过来，然而最后T4并没有骗到分(￣_￣|||)
T1题解上的所有性质啥的都想到了，甚至Miller Rabin都想到了，甚至部分分的分配都想到了，但真的没学过最小割。。但后来发现匈牙利算法也能写，将点根据奇偶性分为两部分，一开始如果一个奇数加一个偶数的和为质数，那么这个奇向偶连边。因为除最大匹配完剩下的就没有可以连的对儿了，也就是我们的答案。有一个小问题就是总点数-最大匹配=最大独立集，好像是跟最小割相关的？不太清楚。
T2也是考场上的思路没有任何问题，并查集也想到了了，但就是代码不是很会写。感觉炸弹和炸弹连比较复杂，还要给它们编号。所以我们不妨换一个思路，连接行和列，那么就会形成一个个连通块。如果一个连通块有环，那么这个块的答案就是包含的行和列的水晶个数，否则还需要减去最小的一列/一行。可以提前算出每个连通块的总个数，以及减掉某一行/列的消耗（注意这里并不单单只是一行/列的个数，比如同一行里有些列的水晶可能连通，有些不通），找最小值只需dfs即可。
点击查看代码
//直接行列连边即可，不用连炸弹，否则会写得很麻烦
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=3005;
int n, m, k, b, minn, cnt[maxn*2], h[maxn*2], fa[maxn*2], a[3005][3005], cir, vis[maxn*2], ans, s[maxn*2];
int find(int x)
{
return x==fa[x]?x:fa[x]=find(fa[x]);
}
void merge(int a,int b)
{
a=find(a), b=find(b);
if(a==b) return ;
fa[a]=b;
}
struct edge{
int next, to;
}edge[maxn*4];
int head[maxn*2], edgenum;
void add(int from,int to)
{
edge[++edgenum].next=head[from];
edge[edgenum].to=to;
head[from]=edgenum;
}
void dfs(int u,int fa)
{
if(vis[u])
{
cir=1;
return ;
}
vis[u]=1;
if(cnt[u]==1) minn=min(minn, h[u]);
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
dfs(v, u);
}
}
signed main()
{
// freopen("boom.in","r",stdin);
cin>>n>>m>>k>>b;
for(int i=1;i<=n+m;i++) fa[i]=i;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
char x;
cin>>x;
if(x=='b')
{
a[i][j]=1;
merge(i, j+n);
add(i, j+n), add(j+n, i);
cnt[i]++, cnt[j+n]++;
}
if(x=='.') a[i][j]=-1;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(a[i][j]==0)
{
s[find(i)]++;
if(find(i)!=find(j+n))
{
s[find(j+n)]++;
h[i]++, h[j+n]++;
}
}
}
}
for(int i=1;i<=n+m;i++)
{
if(vis[i]) continue;
minn=1e18, cir=0;
dfs(i, 0);
if(cir) ans=max(ans, s[find(i)]);
else ans=max(ans, s[find(i)]-minn);
}
cout<<ans;
return 0;
}
/*
3 3 4 2
k..
kk.
bbk
*/
T3真得改地很辛苦，先学Nim游戏，然后是SG函数，然后学SG定理，最后再看题解。网上题解写得也很清楚，必须要赞一下。
整体的思路就是把每个棋子单独考虑，然后求出每个棋子的sg值，然后答案就是把这些棋子的sg异或出来判断即可。
此题首先根据部分分能看出要分成两部分考虑：当前行无障碍和当前行有障碍。
sg函数是要从下往上倒着推的。
注意到棋子只可能往左，往右，往下走，那么sg函数就是由这3个后继状态转来的，求它们的mex即可。
x为当前行，i为当前列。
当前行有障碍：
障碍将这一行分为一段一段的（可以断环为链，首尾相接），然后单独计算每一段，往下走这个后继状态为sg[x+1][i]，接着考虑往左和往右。会发现如果往左走后就不能往右走了，只能一直往左走到上一个障碍（中途也可以往下走），设f[0/1][i]表示从左/右走过来到当前行的第i列的sg值，倒着想一下（具体地，我现在是从右往左想的，求f的时候需要从左往右倒推），那么对于i，它向左边走的后继状态就是f[0][i-1]，右边同理。用这三个值更新即可。
点击查看代码
void solve(int x)
{
for(int i=1;i<=m;i++) c[x][i+m]=c[x][i];//断环为链
int p=1;
for(int i=1;i<=m;i++)
{
if(c[x][i]=='#')
{
p=i;
break;
}
}
memset(f, 0, sizeof(f));
int r=0;
for(int l=p;l<m+p;l=r)
{
r=l+1;
while(r<m+p&&c[x][r]!='#') r++;
if(r==l+1) continue;
f[0][l+1]=mex(sg[x+1][chg(l+1)], -1, -1);
for(int i=l+2;i<r;i++) f[0][i]=mex(f[0][i-1], sg[x+1][chg(i)], -1);
f[1][r-1]=mex(sg[x+1][chg(r-1)], -1, -1);
for(int i=r-2;i>l;i--) f[1][i]=mex(f[1][i+1], sg[x+1][chg(i)], -1);
for(int i=l+1;i<=r-1;i++)
{
if(i==l+1&&i==r-1) sg[x][chg(i)]=mex(sg[x+1][chg(i)], -1, -1);
else if(i==l+1) sg[x][chg(i)]=mex(sg[x+1][chg(i)], f[1][i+1], -1);
else if(i==r-1) sg[x][chg(i)]=mex(sg[x+1][chg(i)], f[0][i-1], -1);
else sg[x][chg(i)]=mex(sg[x+1][chg(i)], f[1][i+1], f[0][i-1]);
}
}
}
当前行无障碍：
感觉麻烦了很多。
没有障碍后整个行都是联通的，还是保持原有思路不变，考虑向左，向右，向下的后继状态。向下就不需要说了。我们先考虑向左的，向左走和上面一样，但因为没有障碍了所以形成一个环，不断往左走最终会到i+1这个位置，它左右都无法走（因为i是需要更新的，不能再往左走了），它的后继状态只有向下的，把这个值求出来后，倒着推一遍（也就是不断和向下的后继状态去取mex），最后退回我们想要的值。
但因为这样写的话求每一个i都是O(m)的，考虑优化。仔细想想其实可以把这个不断向左走的过程划分为2个段：1i,i+1m。如果我们可以提前预处理出这两段的倒推就好了，但我们预处理时不知道最初位置（也就是i+1那个位置）的答案，怎么办？注意打因为sg只是求3个数的mex，它不可能超过3，那我们枚举它的值再求就好啦。还有一点是到1和m这两个分界点比较麻烦，那我直接放题解吧，写不动了。。
点击查看代码
void solve1(int x)
{
if(m==1)
{
sg[x][1]=mex(sg[x+1][1], -1, -1);
return ;
}
memset(g, 0, sizeof(g));
for(int i=0;i<=3;i++)
{
g[0][i][1]=i;
g[1][i][m]=i;
g[2][i][1]=i;
g[3][i][m]=i;
}
for(int i=2;i<=m;i++)
{
for(int j=0;j<=3;j++) g[0][j][i]=mex(g[0][j][i-1], sg[x+1][i], -1);
}
for(int i=m-1;i>=1;i--)
{
for(int j=0;j<=3;j++) g[1][j][i]=mex(g[1][j][i+1], sg[x+1][i], -1);
}
for(int i=2;i<=m;i++)
{
for(int j=0;j<=3;j++) g[2][j][i]=g[2][mex(j, sg[x+1][i-1], -1)][i-1];
}
for(int i=m-1;i>=1;i--)
{
for(int j=0;j<=3;j++) g[3][j][i]=g[3][mex(j, sg[x+1][i+1], -1)][i+1];
}
for(int i=1;i<=m;i++)
{
int t, t1=-1, t2=-1;
int nxt=chg(i+1);
int ed=g[3][mex(sg[x+1][nxt], -1, -1)][nxt];//往回推到m
if(i==1) t1=ed;
else
{
if(i==m) t=mex(sg[x+1][1], -1, -1);
else t=mex(sg[x+1][1], ed, -1);
t1=g[0][t][i-1]; //推到1再推到i-1
}
int lst=chg(i-1+m);
int st=g[2][mex(sg[x+1][lst], -1, -1)][lst];//往回推到1
if(i==m) t2=st;
else
{
if(i==1) t=mex(sg[x+1][m], -1, -1);
else t=mex(sg[x+1][m], st, -1);//推到m再推到i+1
t2=g[1][t][i+1];
}
sg[x][i]=mex(t1, t2, sg[x+1][i]);
}
}
2025/8/22 | 2025CSP-S模拟赛39
link：https://www.gxyzoj.com/d/hzoj/contest/689ea1d8b330a4c3c5799bea/problems
2025/8/23 | 2025CSP-S模拟赛40
link：https://www.gxyzoj.com/d/hzoj/contest/68a28c9db73bee9a8b31a39b/problems
2025/8/25 | 2025CSP-S模拟赛41
link：https://www.gxyzoj.com/d/hzoj/contest/68a41b65b73bee9a8b32c525/problems
嗓子疼，打完就走了。
但还是要写一下T1。
2025/8/26 | 2025CSP-S模拟赛42
link：https://www.gxyzoj.com/d/hzoj/contest/68a51f09b73bee9a8b334ef9/problems
又是全场切T1而我没有的一场ε(┬┬﹏┬┬)3
T1想的离正解挺近的，当时卡在一个点：无法求出以t为根时，s和s'的lca，然而实际上在原树上多求几遍lca即可，还有一个小问题就是判断从s点还是s'点跳祖先的判定写的有点问题。把主函数挂到这里吧。
点击查看代码
dfs(1, 0);
for(int i=1;i<=q;i++)
{
int s, t, s1;
s=read(), t=read(), s1=read();
int lca1=LCA(s, t), lca2=LCA(lca1, s1);
if(lca1==lca2)
{
lca2=LCA(s, s1);
if(lca1==lca2) lca2=LCA(s1, t);
}
else lca2=lca1;
int d1=getdis(s, lca2), d2=getdis(s1, lca2);
if(d1<d2) cout<<getdis(s1, t)<<" "<<t<<"\n";
else
{
int lca=LCA(s, s1);
int d=d1+d2;
if(d/2<=getdis(s1, lca))
{
int p=getk(s1, d/2);
cout<<getdis(p, s)<<" "<<p<<"\n";
}
else
{
int p=getk(s, d-d/2);
cout<<getdis(p, s)<<" "<<p<<"\n";
}
}
}
然后T2考场上想出了一种O(nm)做法，只需考虑每次增加了一个数后增加了多少区间，然后对于当前的i，将当前cnt数组每一位减去整个数组最小的值，如果这一串数以前出现过，那么从以前出现的位置到i这个区间就是合法的。这一串数哈希一下，拿map一存就很简单了。
然后正解是一个很神奇的东西，考虑给每一个a[i]映射一个值，我们大胆定下结论：如果一个区间的和是 1~m映射的值的和 的倍数，它就是合法的。如果这个和是0的话，就相当于这两个区间的前缀和相同，那这就很好求了。考虑让这个和变为0，然后给前缀和排个序，一段长度为cnt的相同段的区间个数就是(cnt-1)*cnt/2，然后代码很短。
T3其实就是不难的dp。考场上写了一个小时没分因为不知道啥是线段交，甚至拿线段树去维护这个，有点想笑了。。。这里我直接放题解吧，反正换我写也是抄一遍。
T4改了一个半小时真的被自己的脑回路气笑了(╬▔皿▔)╯。首先把这个题看成一种场景：每个时刻都会有一个赌徒带着1元钱进入赌场从第一位开始赌，赌这一位的数是什么。如果赌赢了，就给他的钱翻倍，即×m（就相当于从原来的 \(m^i\) 变成 \(m^{i+1}\) ，相当于往后移了一位，接着赌下一位。如果赌输了，那么就把钱就输光给赌场。直到有人把整个B全赌对了（即这个人拿到 \(m^n\) 元钱）赌场就关门了。因为这是一个公平的游戏，那么最后序列长度的期望就是赌场关门时剩下的赌徒的总钱数。然后发现最后剩下的赌徒刚好就是B的border集合（语言表述不清只可意会）。然后求钱数即可。
2025/8/27 | 2025CSP-S模拟赛43
link：https://www.gxyzoj.com/d/hzoj/contest/68a51fa7b73bee9a8b334f91/problems
感觉自己在熬时间。波波的一番话彻底把自己打回原形。好难受啊😭😭😭
晚上已经颓废到一种地步叫做“什么都看不进去”，遂来写总结。
T1赛时1h其实正解就想得差不多了，但当时不会算时间复杂度，以为过不了，然后区间修改写了个树状数组，实际上直接差分就行了。好好笑啊。唉
T2写了个O(n^3)的暴力。它很像以前做过的一道题（可以说是接近一模一样但做法又完全不一样），一个结论就是把与全放到前面，后面全放或肯定是最大值
2025/8/28 | 2025CSP-S模拟赛44
link：https://www.gxyzoj.com/d/hzoj/contest/68ac2565b73bee9a8b367ca8/problems
变成全场都切T1T2而我没有了，大悲。
T1很快想到了二分并且想到check判断大于等于k，但是自己一直绕着n转并且一直在想排序，从第一版的滑动窗口到最后一版的并查集。。然后复杂度巨大且是假的（写了俩小时终于受不了跳了），其实最后是有转化成三维的趋势的，但是还是比较蠢没有直接枚举值域。然后实际上套上一个三维前缀和就可以做到O(R^3 log R)。写三维前缀和时深刻体会到自己贫瘠的想象力，最终依托自己丑陋的绘图技术硬生生的敲式子。连样例都没过就A了。
T2因为T1只看了眼题打了个暴力就跑路了，当时确实是没往逆序对方面想，也没有观察大洋里。然后这个题首先就是判断-1，如果B中出现A中没有的逆序对，显然无解。接下来就考虑把A中B没有的逆序对消掉。考虑遍历A数组，找到b[i]对应的在A的位置(p)，将i到p的所有数冒泡排序两两交换一下（注意是倒序，才能确保p移到i），但是如果中间有移不了的，他就是不合法的情况。break掉即可。
T3是推式子题。首先把小于这个m进制数分成n部分，例如\((2136)_{10}\)，把它分成1--1999、2000--2099、2100--2129、2130--2136，这几部分的数可以看作长度为n-i+1，首位小于m进制下的第i位，其他位小于m，总和为 s-前缀和 的数，只要能求出满足这样条件的数的数量即可。先不考虑首位的限制，计算所有位都小于m的数量。考虑容斥，设有k个数大于等于m，那么利用插板法即可求出。剩下的就放题解啦。
T4其实是很锻炼代码能力的题！但感觉被自己浪费了，算了。
首先就是只考虑只有一个银行的情况。我们考虑每一条边有多少贡献。一条边(u,v)有贡献当且仅当有人经过他，因为银行只可能在v的子树内或x的外面，如果是前者，那么贡献就是(siz[1]-siz[v])w（siz是a[i]的和），否则是siz[v]w，两者去min即可。
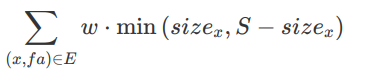
然后回到两个银行的情况。会发现两个银行之间必回有一条边没有人经过（画图证明），枚举这条边，将两头和上面的一样单独计算，时间复杂度O(n^2)。
然后考虑优化。上面那个式子的取min很不好写，发现他其实只需要判断siz[x]是否大于siz[1]/2即可。那这很像权值线段树了，只需要在siz[x]这一位置上加上w，就可以快速查询了。
注意到查询的值还有w*siz[to]，这个也要在线段树上维护好。
然后考虑子树外的，首先子树外的siz只有在v（就是上面那个X的那个to）到根这条链上的点包含siz[v]，所以我们先来算这条链上边的贡献。因为在子树外，所以判定的条件变成(siz[1]-siz[v])/2，但因为我们根本不可能给链的siz都减去siz[v]，那么就把所有值加上siz[v]，把判定条件也加上，就变成 (siz[1]+siz[v])/2，然后就和上面的一样了。注意加上siz[v]多算的要减回来。
然后剩下的就是其他子树（siz里不含siz[v]）的，这部分的和上面一样。
然后全局开一棵线段树维护w和wsiz[v]，链上的用一个树状数组维护w和wsiz[v]，再用一个树状数组维护其他子树的w和w*siz[v]就好了。注意回溯时要撤销。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+5;
int T, n, a[maxn], res, siz[maxn], tot, m, ans;
int head[maxn], edgenum;
struct edge{
int next;
int to;
int w;
}edge[maxn<<1];
void add(int from,int to,int w)
{
edge[++edgenum].next=head[from];
edge[edgenum].to=to;
edge[edgenum].w=w;
head[from]=edgenum;
}
int rt[maxn], idx;
struct seg_tree{
int l, r, sum1, sum2;
}tr[maxn<<6];
void pushup(int id)
{
tr[id].sum1=tr[tr[id].l].sum1+tr[tr[id].r].sum1;
tr[id].sum2=tr[tr[id].l].sum2+tr[tr[id].r].sum2;
}
void update(int &id,int l,int r,int pos,int a,int b)
{
if(!id) id=++idx;
if(l==r)
{
tr[id].sum1+=a;
tr[id].sum2+=b;
return ;
}
int mid=(l+r)>>1;
if(pos<=mid) update(tr[id].l, l, mid, pos, a, b);
else update(tr[id].r, mid+1, r, pos, a, b);
pushup(id);
}
void merge(int &a,int b,int l,int r)
{
if(a==0||b==0)
{
a+=b;
return ;
}
if(l==r)
{
tr[a].sum1+=tr[b].sum1;
tr[a].sum2+=tr[b].sum2;
return ;
}
int mid=(l+r)>>1;
merge(tr[a].l, tr[b].l, l, mid);
merge(tr[a].r, tr[b].r, mid+1, r);
pushup(a);
}
pair<int,int> query(int id,int l,int r,int ll,int rr)
{
if(!id) id=++idx;
if(l>=ll&&r<=rr)
{
return make_pair(tr[id].sum1, tr[id].sum2);
}
int mid=(l+r)>>1;
if(ll>mid) return query(tr[id].r, mid+1, r, ll, rr);
else if(rr<=mid) return query(tr[id].l, l, mid, ll, rr);
else
{
pair<int,int> res=query(tr[id].l, l, mid, ll, mid), res1=query(tr[id].r, mid+1, r, mid+1, rr);
return make_pair(res.first+res1.first, res.second+res1.second);
}
}
struct BIT{
int sum[maxn][2], s1, s2;
int lowbit(int x)
{
return (x&(-x));
}
void clear()
{
memset(sum, 0, sizeof(sum));
s1=s2=0;
}
void add(int pos,int val1,int val2)
{
s1+=val1;
s2+=val2;
while(pos<=m)
{
sum[pos][0]+=val1;
sum[pos][1]+=val2;
pos+=lowbit(pos);
}
}
pair<int,int> query(int pos)
{
pair<int,int> res={0, 0};
while(pos)
{
res.first+=sum[pos][0];
res.second+=sum[pos][1];
pos-=lowbit(pos);
}
return res;
}
}A, B;
void dfs(int u,int fa)
{
siz[u]=a[u];
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
dfs(v, u);
siz[u]+=siz[v];
}
a[u]=siz[u];
}
void dfs1(int u,int fa)
{
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
dfs1(v, u);
int tmp=lower_bound(a+1, a+m+1, siz[v])-a;
A.add(tmp, edge[i].w, siz[v]*edge[i].w);
}
}
void calc(int u)
{
int p=upper_bound(a+1, a+m+1, siz[u]/2)-a-1;
int sum=0;
pair<int,int> res={0ll,0ll};
if(p>=1) res=query(rt[u], 1, m, 1, p);
sum+=res.second+siz[u]*(tr[rt[u]].sum1-res.first)-(tr[rt[u]].sum2-res.second);//u子树内
p=upper_bound(a+1, a+m+1, (siz[1]+siz[u])/2)-a-1;
res=B.query(p);
sum+=res.second+siz[1]*(B.s1-res.first)-(B.s2-res.second)-res.first*siz[u];//链上的边
p=upper_bound(a+1, a+m+1, (siz[1]-siz[u])/2)-a-1;
res=A.query(p);
sum+=res.second+(siz[1]-siz[u])*(A.s1-res.first)-(A.s2-res.second);//其他子树
res={0ll,0ll};
if(p>=1) res=query(rt[u], 1, m, 1, p);
sum-=res.second+(tr[rt[u]].sum1-res.first)*(siz[1]-siz[u])-(tr[rt[u]].sum2-res.second);//u子树内多算的
ans=min(ans, sum);
}
void dfs2(int u,int fa)
{
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==fa) continue;
int tmp=lower_bound(a+1, a+m+1, siz[v])-a;
A.add(tmp, -edge[i].w, -siz[v]*edge[i].w);
B.add(tmp, edge[i].w, siz[v]*edge[i].w);
dfs2(v, u);
B.add(tmp, -edge[i].w, -siz[v]*edge[i].w);
calc(v);
A.add(tmp, edge[i].w, siz[v]*edge[i].w);
update(rt[u], 1, m, tmp, edge[i].w, siz[v]*edge[i].w);
merge(rt[u], rt[v], 1, m);
}
}
void cl()
{
memset(rt, 0, sizeof(rt));
idx=0;
memset(tr, 0, sizeof(tr));
}
signed main()
{
freopen("banking.in","r",stdin);
freopen("banking.out","w",stdout);
cin>>T;
while(T--)
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<n;i++)
{
int u, v, w;
cin>>u>>v>>w;
add(u, v, w), add(v, u, w);
}
ans=1e18;
dfs(1, 0);
sort(a+1, a+n+1);
m=unique(a+1, a+n+1)-a-1;
dfs1(1, 0);
dfs2(1, 0);
cout<<ans<<endl;
for(int i=1;i<=edgenum;i++) edge[i].next=edge[i].to=0;
for(int i=1;i<=n;i++) head[i]=0;
edgenum=0;
A.clear(), B.clear();
cl();
}
return 0;
}
还有1h，我的暑假集训就要结束了。
wme学姐退役了，对我影响还是很深的。上一学期，我第一次有勇气正视了自己对OI的态度。或许是找到同路人，我逐渐意识到，说“不”，其实是很简单的事。没有那么多瞻前顾后，也没有那么多闲言碎语。勇敢一点，大胆一点，何必总是想得小心翼翼。
暑假前，我其实挺害怕（？这个词好像有点过了，那换成担忧吧）的，去年高一的那帮人退役后就没有人给我垫底了⊙﹏⊙∥，很担心自己考砸、考不好、心情郁闷，加上知识进度也很慢，怕自己改不动题（然而事实上把没学过的学一下就好啦呵呵）。这些设想有些确实是发生了，但都没有想象的那么糟糕，甚至过去地和流水一样平淡。更好方面的，这个暑假的代码能力还是有提升的，能写出来一些不敢想的dp了，T1基本可以想到大部分了（虽然T1比去年变简单了），也在不断尝试一些新的东西。成绩的存在感变淡了很多，这些可以说是自己比去年进步的地方。
但是还是经常陷在情绪的深渊啊，我总是觉得自己不够坚定，优柔寡断。坚持集训一暑假，改题时的意志又不够坚定，考试时好像又没有拼尽全力思考。就像 玩没玩好，学没学好 的状态。只能说自己太过情绪化了，有些迷茫，慢慢的熬着，苦痛就像温水煮青蛙一样。但既然我选择了这条路，在没有结束前，我还是希望能尽一点力去做好它，剩下的就交给时间去发酵。
似乎没有去年那样有干劲了，可能只是单纯的心情不好吧，那就用一首歌来收尾吧。。
《普通到不普通的人生》
如果每 一个人 注定要衰老
还不如 留给花园 多一瞬色彩
告诉聪 明的人 笨一些思考
给人生 留一束 鲜花
复杂 世界总创造
不高兴和 没头脑
我却只想 造一只猫
靠漫步 将生趣填饱
心也有一片富饶
快乐就会 笑
不再计较 两脚兽烦恼
一次 也好 任青春消耗
脚下 花草 有日光就好
我想 知道 蝴蝶 柔软的一生 到底能 飞多高
如果每 一个人 注定要衰老
还不如 留给花园 多一瞬色彩
告诉聪明的人 笨一些思考
再葆有 这份热烈 多几个世代
普通到不普通的人
哭着笑着的人
给自己一个拥抱
天生 不会飞的鸟
若努力积攒羽毛
是否就能 爱上风暴
当天空 伸手就碰到
没有人低头祈祷
那你会知道
飞翔没有 行走更重要
世界 很吵 你别太苦恼
那片 花草 晒月光也好
我想 知道 蝴蝶 柔软的一生 到底曾
看过多 美的梦
如果每 一个人 注定要衰老
还不如 留给花园 多一瞬色彩
告诉聪明的人 笨一些思考
再葆有 这份热烈 多几个世代
普通到不普通的人
哭着笑着的人
给自己一个拥抱
儿时的 天空多直白 那么开阔 那么纯净
蹒跚追的 美好憧憬 一眨眼 就远行
绕过云彩 多少我 还活在 天之外
会不会 有不同 的精彩
跟随蝴蝶的飞行 我也能抓住流星
灼伤了眼睛 也会目视着光明
某一个瞬息 我们都吹过同阵 风
如果每 一个人 注定要衰老
还不如 留给花园 多一瞬色彩
告诉聪 明的人 笨一些思考
再葆有 这份热烈 多几个世代
普通到不普通的人
哭着笑着的人
眼泪别流出眼角
希望你能开心一点。😊
All this dinosaurs
世上所有小恐龙is gonna get a crucial extinction
都会面临大灭绝But now they are all with mine
我也和他们一样Self-employing childish ambition
自娱自乐的带着童真的顽皮
浙公网安备 33010602011771号