数据结构学习笔记

1.单调栈、队列、优先队列

1）单调栈：单调递增或单调递减的栈。

它适用于找左边/右边第一个比自己大的元素(位置)。

优点：时间复杂度为O(n)。

模版题：洛谷 5788

2）单调队列：单调递减或单调递增的队列。

它能够动态地维护定长序列中的最值。

优点：可以降低时间复杂度。

模版题：洛谷 P1886

3）优先队列：在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出（first in, largest out）的行为特征。通常采用堆数据结构来实现。

它适用于动态维持有序状态的场景。

模版题：洛谷 P3378

2.树状数组

树状数组结合了树的思想,常用来处理前缀问题。

优点：修改和查询节点的复杂度都是O(logN)。

模版题：洛谷 P3374 P3368

一维：

点击查看代码

#define lowbit(x) (x&(-x))
int sum[maxn];
void add(int pos,int val)
{
	while(pos<=n)
	{
		sum[pos]+=val;
		pos+=lowbit(pos);
	}
}
int query(int pos)
{
	int res=0;
	while(pos>0)
	{
		res+=sum[pos];
		pos-=lowbit(pos);
	}
	return res;
}

二维：

点击查看代码

long long lowbit(int x)
{
	return x&(-x);
}
void add(int x,int y,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		for(int j=y;j<=m;j+=lowbit(j))
		{
			s[i][j]+=k;
		}
	}
}
long long getsum(int x,int y)
{
	long long ans=0;
	for(int i=x;i;i-=lowbit(i))
	{
		for(int j=y;j;j-=lowbit(j))
		{
			ans+=s[i][j];
		}
	}
	return ans;
}
void add(int x,int y,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		for(int j=y;j<=m;j+=lowbit(j))
		{
			c1[i][j]+=k;
			c2[i][j]+=x*k;
			c3[i][j]+=y*k;
			c4[i][j]+=x*y*k;
		}
	}
}
int getsum(int x,int y)
{
	int ans=0;
	for(int i=x;i;i-=lowbit(i))
	{
		for(int j=y;j;j-=lowbit(j))
		{
			ans+=(x+1)*(y+1)*c1[i][j]-(y+1)*c2[i][j]-(x+1)*c3[i][j]+c4[i][j];
		}
	}
	return ans;
}

树状数组求逆序对：

点击查看代码

cin>>n;
for(int i=1;i<=n;i++)
{
	cin>>a[i];
	maxx=max(maxx, a[i]);
}
for(int i=1;i<=n;i++)
{	
	t1[i]=query(maxx)-query(a[i]);
	add(a[i], 1);
}

3.线段树

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

普通线段树：

点击查看代码

#include<bits/stdc++.h>
#define int long long 
#define lid (id<<1)
#define rid (id<<1|1)
using namespace std;
const int maxn=5e5+5;
int n, m, a[maxn], x, y, z;
string b;
struct seg_tree{
	int l, r;
	int sum, lazy;
}tr[maxn<<1]; 
void pushup(int id)
{
   tr[id].sum=tr[lid].sum+tr[rid].sum;
}
void build(int id, int l, int r) //建树 
{
	tr[id].l=l;
	tr[id].r=r;
	if(l==r)
	{
		tr[id].sum=a[l];
		return ; 
	}
	int mid=(l+r)>>1;
	build(lid, l, mid);
	build(rid, mid+1, r);
	pushup(id);
}
void update(int id,int l,int k)//单点修改
{
	if(tr[id].l==tr[id].r)
	{
		tr[id].sum+=k;
		return ;
	}
	int mid=(tr[id].r+tr[id].l)>>1;
	if(mid>=l) update(lid,l,k);
	else update(rid,l,k);
	pushup(id);
}
void pushdown(int id) //下放lazy 
{
	if(tr[id].lazy&&tr[id].l!=tr[id].r)
   	{
		tr[lid].lazy+=tr[id].lazy;
		tr[rid].lazy+=tr[id].lazy;
		tr[lid].sum+=tr[id].lazy*(tr[lid].r-tr[lid].l+1);
		tr[rid].sum+=tr[id].lazy*(tr[rid].r-tr[rid].l+1);
		tr[id].lazy=0;
	}
}
void modify(int id, int l, int r, int val)//区间修改 
{
	pushdown(id);
	if(tr[id].l>=l&&tr[id].r<=r)
	{
		tr[id].lazy+=val;
		tr[id].sum+=val*(tr[id].r-tr[id].l+1);
		return ;
	}	
	int mid=(tr[id].l+tr[id].r)>>1;
	if(r<=mid)	modify(lid, l, r, val);
	else if(l>mid)	modify(rid, l, r, val);
	else
  	{
 		modify(lid, l, mid, val);
		modify(rid, mid+1, r, val);
	}
	pushup(id);
}
int query(int id,int l, int r) //区间查询 
{
	pushdown(id);
	if(tr[id].l>=l&&tr[id].r<=r)
	{
		return tr[id].sum;
	}
	int mid=(tr[id].l+tr[id].r)>>1;
	if(r<=mid) return query(lid, l, r);
	if(l>mid) return query(rid, l, r);
	return query(lid,l,mid)+query(rid,mid+1,r);
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];		
	}
	build(1,1,n);
	cin>>m;
	for(int i=1;i<=m;i++)
	{	
		cin>>b;
		if(b=="ADD")
		{
			cin>>x>>y>>z; 
			modify(1, x, y, z);
		}
  		else
		{
 			cin>>x>>y;
			cout<<query(1,x,y)<<endl;
		}
	}
	return 0;
}

维护最大子段和（应该是对的）

#include<bits/stdc++.h>
#define lid id<<1
#define rid id<<1|1
using namespace std;
const int maxn=1e5+10;
int n, m, a[maxn];
struct seg_tree{
	int ms, ls, rs, s;//最大子段和,区间紧靠左端点的最大子段和,区间紧靠左端点的最大子段和,区间子段和  
}tr[maxn<<2];
void pushup(int id)
{
	tr[id].ms=max(max(tr[lid].ms, tr[rid].ms), tr[lid].rs+tr[rid].ls);
	tr[id].ls=max(tr[lid].ls,tr[rid].ls+tr[lid].s);
	tr[id].rs=max(tr[rid].rs,tr[lid].rs+tr[rid].s);
	tr[id].s=tr[lid].s+tr[rid].s;
}
void build(int id,int l,int r)
{
	if(l==r)
	{
		tr[id].ms=tr[id].ls=tr[id].rs=tr[id].s=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(lid, l, mid);
	build(rid, mid+1, r);
	pushup(id);
}
void add(int id,int l,int r,int u,int v)
{
	if(l==r)
	{
		tr[id].ms=tr[id].ls=tr[id].rs=tr[id].s=v;
		return ;
	}
	int mid=(l+r)>>1;
	if(u<=mid)
	{
		add(lid, l, mid, u, v);
	}
	else
	{
		add(rid, mid+1, r, u, v);
	}
	pushup(id);
}
seg_tree query(int id,int l,int r,int ql,int qr)
{
	if(ql<=l&&r<=qr)
	{
		return tr[id];
	}
	seg_tree x, y, w;
	int mid=(l+r)>>1;
	if(qr<=mid)
	{
		w=query(lid, l, mid, ql, qr);
	}
	else if(ql>mid) 
	{
		w=query(rid, mid+1, r, ql, qr);
	}
	else
	{
		x=query(lid, l, mid, ql, mid);
		y=query(rid, mid+1, r, mid+1, qr);
		w.s=x.s+y.s;
		w.ls=max(x.ls, x.s+y.ls);
		w.rs=max(y.rs, y.s+x.rs);
		w.ms=max(max(x.ms, y.ms), x.rs+y.ls);
	}
	return w;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	cin>>m;
	build(1, 1, n);
	for(int i=1;i<=m;i++)
	{
		int x, y, z;
		cin>>x>>y>>z;
		if(x==0) add(1, 1, n, y, z);
		else 
		{
			seg_tree x=query(1, 1, n, y, z);
			cout<<x.ms<<endl;
		}
	}
	return 0;
}

线段树做题技巧：

一般需要线段树优化的题有一些特点：

有明显的修改和查询操作，考虑该如何转换。
有类似于合并的操作，一段区间的值与两个端点的合并有关。
直接考虑计算时间复杂度。
遇到要求一些满足特殊要求的子序列、子串长度，考虑维护最大子段和版线段树。

线段树怎么写：

线段树要维护的就是与答案相关的值（一般都是能协助区间合并的），就像dp状态设计一样，例如山海经中的最大子段和、区间前后缀等等。
合并可能会很复杂，考虑分类讨论，一定要全面。
剩下的直接套板子。

请原谅我马蜂突变(已修改），因为实在找不到固定的板子（
我已经尽力在补救了。

动态开点线段树

点击查看代码

struct seg_tree{
	int l, r, sum, maxx, lazy;
}tr[maxn<<4];
void pushup(int id)
{
	tr[id].maxx=max(tr[tr[id].l].maxx, tr[tr[id].r].maxx);
	tr[id].sum=tr[tr[id].l].sum+tr[tr[id].r].sum;
}
void pushdown(int id,int l,int r)
{
	if(tr[id].lazy)
	{
		if(!tr[id].l) tr[id].l=++cnt;
		if(!tr[id].r) tr[id].r=++cnt;
		int mid=(l+r)>>1;
		tr[tr[id].l].lazy+=tr[id].lazy;
		tr[tr[id].r].lazy+=tr[id].lazy;
		tr[tr[id].l].sum+=tr[id].lazy*(mid-l+1);
		tr[tr[id].r].sum+=tr[id].lazy*(r-mid);
		tr[id].lazy=0;
	}
}
void update(int &id,int l,int r,int p,int val)//单点修改 
{
	if(!id) id=++cnt;
	if(l==r)
	{
		tr[id].sum=tr[id].maxx=val;
		return ;
	}
	int mid=(l+r)>>1;
	if(p<=mid) update(tr[id].l, l, mid, p, val);
	else update(tr[id].r, mid+1, r, p, val);
	pushup(id);
}
void updata(int &id,int l,int r,int ll,int rr,int val)//区间修改 
{
	if(!id) id=++cnt;
	if(r<ll||l>rr) 	return ;
	if(ll<=l&&r<=rr)
	{
		tr[id].sum+=(r-l+1)*val;
		return ;
	}
	int mid=(l+r)>>1;
	pushdown(id, l, r);
	updata(tr[id].l, l, mid, ll, rr, val);
	updata(tr[id].r, mid+1, r, ll, rr, val);
} 
int query(int id,int l,int r,int ll,int rr)
{
	if(!id) return 0;
	if(r<ll||l>rr) 	return 0;
	if(l>=ll&&r<=rr) return tr[id].sum;
	int mid=(l+r)>>1;
	if(rr<=mid) return query(tr[id].l, l, mid, ll, rr);
	else if(ll>mid) return query(tr[id].r, mid+1, r, ll, rr);
	else return query(tr[id].l, l, mid, ll, mid)+query(tr[id].r, mid+1, r, mid+1, rr);
}

线段树合并与分裂

下面的操作大都是在权值线段树（就是一个桶）上进行的。

前置知识：一颗权值线段树的叶子节点维护的是“有几个1”、“有几个2”。。。
支持操作：

添加一个元素
查找一个元素出现次数
查找区间的元素个数
查询所有元素的第k大/小的元素

线段树合并：

就是将树的信息相加，原理很简单，就是将对应位置的点相加即可。

点击查看代码

int merge(int a, int b,int l,int r) 
{
	if(!a||!b) 
	{
		return a+b;
	}
	if(l==r) 
	{
		tr[a].num+=tr[b].num;
		del(b);
		return a;
	}
	int mid=(l+r)>>1;
	tr[a].l=merge(tr[a].l, tr[b].l, l, mid);
	tr[a].r=merge(tr[a].r, tr[b].r, mid+1, r);
	pushup(a);
	del(b);
	return a;
}

还有这一版

点击查看代码

//未修整
int merge(int a, int b) 
{
	if(!a||!b) 
	{
		return a+b;
	}
	int p=++cnt;
	if(l==r) 
	{
		tr[p]=tr[a]+tr[b];
		return p;
	}
	int mid=(l+r)>>1;
	tr[p]=tr[a]+tr[b];
	ls[p]=merge(ls[a], ls[b], l, mid);
	rs[p]=merge(rs[a], rs[b], mid+1, r);
	return p;
}

线段树分裂：

是将以 a 为根的线段树中保留排名为 1 到 k 中的数而把其他值给以 b 为根的线段树中。

点击查看代码

void split(int a,int &b,int k)
{
	if(!a) return ;
	b=newnode();
	int v=tr[tr[a].l].num;
	if(k>v) split(tr[a].r, tr[b].r, k-v);
	else swap(tr[a].r, tr[b].r);
	if(k<v) split(tr[a].l, tr[b].l, k);
	tr[b].num=tr[a].num-k;
	tr[a].num=k;
}

4.树链剖分

树剖是通过轻重边将树分割成多条链，然后利用数据结构来维护这些链（本质上是一种优化暴力）。

一些概念和性质

重儿子：父亲节点的所有儿子中子树结点数目最多的节点。

轻儿子：父亲节点中除了重儿子以外的儿子。

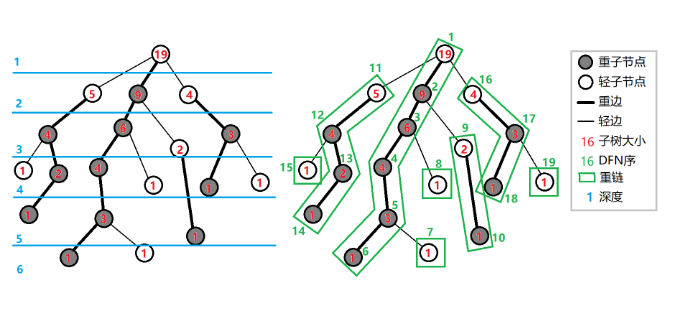
批注 2025-10-31 095947

其他什么的也不用解释了。

整棵树会被剖分成若干条重链。
轻儿子一定是每条重链的顶点。
任意一条路径被切分成不超过 \(logn\) 条链。
重链的各个节点的dfs序都是连续的。

重链剖分有一些性质，这些性质正是它在动态 DP 中能够发挥作用的重要保障。

每个点到根的路径上，最多经过 logn 条轻边。也就是说，重链的条数最多也只有 logn 条。这为动态 DP 的时间复杂度做了保障。
每条重链的链尾都是叶子节点，且只有叶子节点没有重儿子。这为动态规划的初始状态和转移方式做了保障。
重链剖分中，一条重链所在的区间在剖出的 DFS 序上，是连续的一段区间。这为可以使用数据结构维护区间信息，达到快速转移做了保障。

板子：

点击查看代码

struct edge{
	int next,int to;
}edge[maxn<<1];
struct node{
	int sum, lazy, l, r, lid, rid;
}node[maxn<<1];
int rt, n, m, r, a[maxn], cnt, d[maxn], f[maxn], head[maxn];
int size[maxn], son[maxn], rk[maxn], top[maxn], dfn[maxn];
//d:深度 f:父节点 size:子树节点个数 son:重儿子 
//rk:当前dfs标号在原树中所对应的节点编号 top:当前节点所在链的顶端节点
//dfn:每个节点剖分后的新编号 
void dfs1(int u,int fa,int dep)//处理出f,size,son,d数组 
{
	f[u]=fa;
	d[u]=dep;
	size[u]=1;
	for(int i=head[u];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa) continue;
		dfs1(v,u,dep+1);
		size[u]+=size[v];
		if(size[v]>size[son[u]])
		{
			son[u]=v;
		}
	}
}
void dfs2(int u,int t)//处理出top,dfn,rk数组 (t表示重链顶端） 
{
	top[u]=t;
	dfn[u]=++cnt;
	rk[cnt]=u;
	if(!son[u]) return ;
	dfs2(son[u],t);
	for(int i=head[u];i;i=edge[i].next)//轻链 
	{
		int v=edge[i].to;
		if(v!=son[u]&&v!=f[u])
		{
			dfs2(v,v);
		}
	}
}

求LCA

点击查看代码

int LCA(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x, y);
		x=f[top[x]];
	}
	if(dep[x]<dep[y]) return x;
	else return y;
}

查找

点击查看代码


int qsum(int u,int v)
{
	int res=0;
	while(top[u]!=top[v])
	{
		if(dep[top[u]]<dep[top[v]]) swap(u, v);
		res+=query(rt, 1, n, dfn[top[u]], dfn[u]);
		u=f[top[u]];
	}
	if(dep[u]<dep[v]) swap(u, v);
	res+=query(rt, 1, n, dfn[v], dfn[u]);
	return res;
}

边权放点权

点击查看代码

#include<bits/stdc++.h>
#define lid (u*2)
#define rid (u*2+1)
using namespace std;
const int maxn=1e5+10;
int n,cnt, x[maxn], y[maxn], z[maxn];
int dian[maxn];
int a[maxn];
int son[maxn],f[maxn],size[maxn],top[maxn],d[maxn],rk[maxn],dfn[maxn];
int tr[maxn<<2];
struct edge{
	int next,to,w;
}edge[maxn<<1];
int head[maxn], edgenum;
void add(int from,int to,int w)
{
	edge[++edgenum].next=head[from];
	edge[edgenum].to=to;
	edge[edgenum].w=w;
	head[from]=edgenum;
}
void dfs1(int u,int fa)
{
	f[u]=fa;
	d[u]=d[fa]+1;
	size[u]=1;
	for(int i=head[u];i;i=edge[i].next)
	{
		int y=edge[i].to;
		if(y==fa) continue;
        a[y]=edge[i].w;
		dfs1(y,u);
		size[u]+=size[y];
		if(size[y]>size[son[u]])
		{
			son[u]=y;
		}
	}
}
void dfs2(int u,int t)
{
	top[u]=t;
	dfn[u]=++cnt;
	rk[cnt]=u;
	if(son[u]) 
	{
		dfs2(son[u],t);
	}
	for(int i=head[u];i;i=edge[i].next)
	{
		int y=edge[i].to;
		if(y!=son[u]&&y!=f[u])
		{
			dfs2(y,y);
		}
	}
}
void build(int u,int l,int r)
{
    if(l==r)
    {
        tr[u]=a[rk[l]];
        return;
    }
    int mid=(l+r)>>1;
    build(lid,l,mid);
    build(rid,mid+1,r);
    tr[u]=max(tr[lid],tr[rid]);
    return;
}
void updata(int u,int l,int r,int pos,int z)
{
    if(l==r)
    {
        tr[u]=z;
        return;
    }
    int mid=(l+r)>>1;
    if(pos<=mid)
    {
    	updata(lid,l,mid,pos,z);
	}
    else 
    {
    	updata(rid,mid+1,r,pos,z);
	}
    tr[u]=max(tr[lid],tr[rid]);
}
int mx(int u,int l,int r,int ql,int qr)
{
    if(ql>r||qr<l)
    {
    	return -1e9;
	}
    if(ql<=l&&r<=qr)
    {
    	return tr[u];
	}
    int mid=(l+r)>>1;
    return max(mx(lid,l,mid,ql,qr),mx(rid,mid+1,r,ql,qr));
}
int qsum(int x,int y)
{
    int res=-1e9;
    while(top[x]!=top[y])
    {
    	if(d[top[x]]<d[top[y]])
    	{
    		swap(x,y);
		}
        res=max(res,mx(1,1,n,dfn[top[x]],dfn[x]));
        x=f[top[x]];
    }
    if(d[x]>d[y])  swap(x,y);
    res=max(res,mx(1,1,n,dfn[x]+1,dfn[y]));
    return res;
}
int main()
{
    cin>>n;
    for(int i=1;i<n;i++)
    {
        cin>>x[i]>>y[i]>>z[i];
        add(x[i], y[i], z[i]);
        add(y[i], x[i], z[i]);
    }
    dfs1(1,0);
    dfs2(1,1);
    for(int i=1;i<n;i++)
    {
    	if(d[x[i]]>d[y[i]])
    	{
    		swap(x[i], y[i]);
		}
	}
    build(1,1,n);
    string s;
    while(cin>>s)
    {
        if(s[0]=='D') break;
        if(s[0]=='C')
        {
            int x,z;
            cin>>x>>z;
            updata(1,1,n,dfn[y[x]],z);
        }
        if(s[0]=='Q')
        {
            int x,y;
            cin>>x>>y;
            cout<<qsum(x, y)<<endl;
    	}
    }
    return 0;
}

有时间再来好好修整一下

posted @ 2025-02-16 14:57 zhouyiran2011 阅读(38) 评论(0) 收藏举报

刷新页面返回顶部

zhouyiran2011

数据结构学习笔记

1.单调栈、队列、优先队列

2.树状数组

3.线段树

线段树合并与分裂

线段树合并：

线段树分裂：

4.树链剖分

一些概念和性质

公告