专项训练1

暑假训练快结束了，突然又想整个这个，零散的刷题时间也要积累起来，万一以后忘了呢。。。

数据结构专题

1. [SNOI2017]一个简单的询问

link：https://www.luogu.com.cn/problem/P5268

从来没有见过这么水的蓝题，一眼莫队板题，分开维护两个区间的和，加入一个数就减去原来的贡献，加上增加的贡献。删除亦然。

Tips：

块长要设为1000，会影响复杂度。
排序按 \(l1,r1,l2,r2\) 关键字排。

2. [USACO19DEC] Bessie's Snow Cow P

link：https://www.luogu.com.cn/problem/P5852

set+线段树。会发现如果点 u 已经染过A种颜色，那它的子孙就没必要再染了。所以给每个颜色开个 set 来存储染上这种颜色的点，暴力删除 set 里它的子孙，并加入这个节点。大概就是这样一个思路：

假设现在正在进行一个修改操作，将 x 染成 col 色：

找到 set 中 x 的前一个点，判断其是否是 x 的祖先，如果是的话直接 continue 跳过本次操作。
通过 set 找到 x 子树中已经被染上 col 色的节点。
将这些节点的子树权值总体减 1，同时把这些节点移出 set。
将 x 放入对应的 set，同时将 x 子树中的节点权值总体加 1。

Tips：

线段树大坑，一定要好好检查。
set 是个很好用的东西，平常写代码时可以尝试一下。

3. [十二省联考 2019] 春节十二响

link：https://www.luogu.com.cn/problem/P5290

也不算太难。考虑贪心思想，大的和大的分成一段，小的和小的分。而考虑到不能有祖先--子孙关系，所以就是和父亲节点的其他儿子合并。用大根堆存储两个子树的答案，合并时取出堆顶，比较两个堆顶并得出最大值，把这些值再放入较大一点的堆里面，至于为什么要放到较大堆里面，可以用启发式合并来证明。

让高度小的树成为高度较大的树的子树，这个优化可以称为启发式合并算法。

摘自 OI-WiKi 。

Tips：注意 long long。

4. [SDOI2011] 消防

link：https://www.luogu.com.cn/problem/P2491

树的直径有这一结论：对于任意树上的节点 , 距离其最远的点一定为树的直径的端点。

所以整两个dfs把树的直径求出来。具体的，先从根节点跑一遍，求出直径的一个端点p，再从 p 跑一遍，即可求出另一个端点。

然后采用尺取法（移动区间），可以计算出在所有满足条件的最优情况下，最大值的最小值。（其实就是维护两个指针，根据s调整指针，再用记录这两个指针距离两个端点的距离的最大值的最小值）

但最远距离还可能是直径外的，所以再在直径的每个节点dfs一遍即可。

放一下代码吧：

dfs：

点击查看代码

void dfs(int u,int fa)
{
	f[u]=fa;
	if(len[u]>len[p]) p=u;
	for(int i=head[u];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa||vis[v]) continue;
		cout<<v<<endl;
		len[v]=len[u]+edge[i].w;
		dfs(v, u);
	}
}

尺取法：

点击查看代码

for(int i=p, j=p;i;i=f[i])
{
	while(len[j]-len[i]>s) j=f[j];
	ans=min(ans, max(len[i], len[p]-len[j]));
}

Tips：

最后搜索的时候要标记一下直径上的点。避免重复。
注意到 f 数组，存的不是父亲节点，而是直径上的前驱节点。

5. [HNOI2016] 序列

link：https://www.luogu.com.cn/problem/P3246

看着明显是一个莫队，~~但也可以强制在线~~。难点就是转移，从 \([l,r]\) 向 \([l,r+1]\) 转移，每次转移的变化由两部分组成：\([l,p]\) 和 \([p+1, r]\) ( p 是这个区间最小值)，前者贡献很好算，后者可以用dp求解，搞一搞dp式子可以发现它能预处理出来。

具体的：
设 \(f[l][r]\) 表示以 \(r\) 为右端点，左端点在 \([l,r]\) 的区间的答案(要求的就 \(f[p+1[r+1]\) )，记录一下 \(pre_i\) 表示从 \(i\) 向前第一个比 \(i\) 小的数的位置(这个可以单调栈O(n)求出)，那么左端点在 \([pre_r,r]\) 的区间最小值都是 \(a[r]\) ，那么就有 \(f[l][r]=f[l][pre_r]+a_r×(r-pre_r)\)。

可以发现 \(dp\) 增量只和 \(r\) 自身有关，所以可以去掉 \(l\) 那一维，因为最终一定会存在一个点
\(x\) ，满足 \(pre_x=p\)，那么 \(f_{r+1}=a_{r+1}×(r+1-pre_{r+1})+…+a_x×(x-p)+f_p\) 。

我们可以发现 \(f_{r+1}-f_p\) 就是原来要求的 \(f[p+1][r+1]\)。

RMQ：https://blog.csdn.net/qq_41311604/article/details/79900893

数论专题

明显刷题吃力了很多。。。数论还是我的弱项。

1. [ABC281G] Farthest City

link：https://www.luogu.com.cn/problem/AT_abc281_g

一层一层递推过来，dp[i][j]表示总共i个点，最后一层有j个点的方案数。

有dp转移式：\(dp[i][j]+=dp[i-j][k]*C_{n-i+j-1}^{j}*(2^k-1)^j*2^{C_j^2}\)。

k就是枚举前面每一层的最后一层的点数，\((2^k-1)^j\) 表示每个点向前面的k个点连线：\(C_k^1,C_k^1...C_k^k\) ，共有 \((2^k-1)^j\) 种方案。\(2^{C_j^2}\) 表示j内部的连线，共有 \(C_j^2\) 种连线，有 \(C_{C_j^2}^0,C_{C_j^2}^1...C_{C_j^2}^{C_j^2}\) 种方案数。

自己只推出来一半，剩下的式子还是推不出来。考虑的不够全面，还有所欠缺。

Tips：

二项式定理很重要，不要忘了。
TLE 要预处理。
取模别炸。

2. [ABC305G] Banned Substrings

link：https://www.luogu.com.cn/problem/AT_abc305_g

由于AC自动机学得比较晚，所以印象还是较为深刻的。~~但矩阵快速幂是真的忘得一干二净了~~。

考虑将所有不能匹配的串构建到AC自动机上，\(dp[i][son[u][1/0]]\) 表示到T的第i位，当前在u节点，下一个节点是a/b的方案数。注意到这是不能匹配的，做以维护一个数组记录每个点是否有结束标记，构建矩阵，用矩阵快速幂来优化，递推dp转移。

Tips：注意RE。

此题并未完全掌握，务必在学习AC自动机时再看一遍！！！

3. [CQOI2016] 密钥破解

link：https://www.luogu.com.cn/problem/P4358

虽然学新知识是好事，但这个 \(Pollard\,rho\) 给我看的够呛。

\(Pollard\,rho\) 算法

可以利用这种算法将N分解，就~~很轻松地~~得到p和q，根据扩展欧几里德定理即可求出d和n。

发现自己的扩欧学得还是不扎实，唉，赶紧填坑吧。

4. [NOI2018] 屠龙勇士

link：https://www.luogu.com.cn/problem/P4774

一眼excrt。

根据数据范围给出的表格，我们可以迅速发现 p 数组（有一个点都为质数）即为模数，就能立马推出式子：\(a[i]≡x*atk[i] (mod\,p[i])\)，发现和普通的excrt的区别就是多带了个*x，因为模数不一定为质数，所以我们无法用逆元求解，所以就考虑从excrt的本质操作入手。

excrt的过程其实就是两两联立相邻的两行方程，用扩欧求解，方程为：\(lcm*x+p_i*y=(a_i-ans)\) ，总共有 n-1 次合并，将 atk[i] 带入里面推式子，发现式子变为 \(atk_i*lcm*x+p_i*y=a_i-atk_i*ans\) ，也就多带了个 atk[i] ，所以直接改变excrt函数即可。

杀死每条龙的剑提前预处理即可，用multiset。

5.「雅礼集训 2018 Day10」足球大战

link：https://gxyzoj.com/d/hzoj/p/3990

其实是一道很简单的概率题，枚举主队和客队的赢的场数，直接递推即可，式子即为：

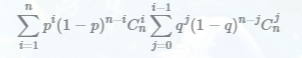
但是由于数据范围（1e7），要先预处理，边计算边枚举i，注意卡常。

Tips：

开两个1e7的数组会炸空间，但由于组合数都只需要n的阶乘，所以用一个数来存储 \(n!\)。
求逆元的写法可能会被卡，考虑换写法（详见数论）。

DP杂项

1. [PA2021] Od deski do deski

link：https://www.gxyzoj.com/d/hzoj/p/4096?tid=6709f0bc723564e75e98eb21

小清新dp，但状态设定很不好想。感觉它是从dp的推导设定的，会发现删除操作没有交集，设 \(f[i][j][1/0]\) 代表长度为 i 的序列，在后面放 j 种数可以变成合法的，当前是否合法。答案显然为 \(∑f[n][i][1]\) 。

转移就是分类讨论，讨论这一位是否合法，填表法和刷表法都可以，大概就是这样（其实是太懒不想写：

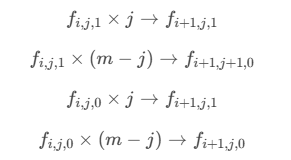
2. [TJOI2019] 甲苯先生的字符串

link：https://www.gxyzoj.com/d/hzoj/p/4119?tid=6709f0bc723564e75e98eb21

看到一个1e15，直接想到矩阵快速幂。

基础 dp 很好想， \(dp[i][j]\) 表示到第 i 位，且当前位为 j 的方案数，显然 \(dp[i][j]=\sum_{j=1}^{26}dp[i-1][j]*check[i][j]\) ，其中 \(check[i][j]\) 为1/0，ij是 s1 的子串即为0，否则为1。

考虑矩阵加速，可以不看第1维，把它想象成每一次的转移。初始矩阵是这个样子（共26列）：\begin{bmatrix}
1 & 1 & 1 & 1 & ... &1 & 1 &1
\end{bmatrix}

转移矩阵（设为X）其实就是上面的 check 数组，第 i 行第 j 列就是0/1，ij是 s1 的子串即为0，否则为1。

所以答案即为上面第一个矩阵* \(X^{n-1}\) ，最后将这个结果矩阵的每一个值加起来即可。

Tips：对角线为1，其余为0的矩阵 \(\times\) 任意矩阵 A 结果都为 A。

3. [ABC213G] Connectivity 2

link：https://www.gxyzoj.com/d/hzoj/p/778?tid=6709f0bc723564e75e98eb21

这个题是在改完前一次考试题后写的，所以写起来很流畅，很快就A了，题解思路很经典，一定要好好整理。

数据一看就是状压，每一位表示这个点是否删去，设两个数组f和g，f[s]表示s里的连通子集的个数，g[s]表示s里的子集个数。显然用g数组更新f数组。

DP专题

1. [NOIP2021] 数列

link：https://www.luogu.com.cn/problem/P7961
发现n的范围极小，只有30，就可以考虑 \(O(n^4)\) 的复杂度。

因为在计算S的二进制表示时会有进位的现象，考虑从低位到高位转移，设 \(dp[i][j][k][p]\) 表示到S从低到高的第i为，已经确定了j个序列里a中的元素，前i位中有k个1，要向下一位进位p。

采取刷表法。

废，写不完了，等未来某一天再补吧。

2. [ABC234G] Divide a Sequence

link：https://www.luogu.com.cn/problem/AT_abc234_g

3. [春季测试 2023] 圣诞树

link：https://www.luogu.com.cn/problem/P9119

图论专题

图论杂项

1.「NOIP2013」华容道

link：https://www.gxyzoj.com/d/hzoj/p/P438?tid=670db460723564e75e9b760d、

自己先写的爆搜，因为太暴力了，而且是dfs，只拿到10分。优化一下应该能拿到更高。暴力思路没啥问题，发现TLE的主要问题在于枚举了很多和目标格子没有任何关系的状态，考虑抽离出这些状态，建边跑最短路即可。

具体的，大概分为以下几个步骤：

预处理
- 空白格子乱转（建边）
- 空白格子和指定格子互换（建边）
让空白格子跑到指定格子周围
跑最短路

代码比较长，调了一早上才过，很多细节要注意。

2. Star Way To Heaven

link：https://www.gxyzoj.com/d/hzoj/p/P824?tid=670db460723564e75e9b760d

首先明确一下：走的路径是可以弯曲的，不一定非要走直线！！！

第一眼看完真的是一点思路都没有，考虑将第一个star和上届连接，最后一个star和下界连接，中间的star互相连接，大概就是把这个矩形分成两半，因为要求最小距离的最大值，肯定是最短路径中间最大的那一条分一半（最优策略肯定是走终点）的值。也就是求最小生成树的最大边权。代码实现很清奇，不能说写了prim，而是用了这种思想。

3. Berland and the Shortest Paths

link：https://www.luogu.com.cn/problem/CF1005F

最短路径树是一个图的生成树，该树有一个原点s，使得对于每个节点，都有对于其任何一个节点 i，都有在原图中s到i的最短路等于在该树中 s 到 i 的距离，而在满足上述条件后，要求使得树的边权和最小。

然后这个题求的就是最短路径树的方案数，我们可以把最终到1的最短路径上每个点所连的边存到这个点的vector里（用dij边跑边更新），那么答案就是所有点vector大小的乘积，方案数用dfs输出即可。

贪心专项

1.「NOIP2012」国王游戏

link：https://www.luogu.com.cn/problem/P1080

好久都没有做绿题了。显然这个题最好做到a、b值都升序（可以通过这些思路骗到50pts）现在单独考虑两个人的情况：

假设这两个人手上的数为（num表示前面所有人a的乘积）：

\(a\) \(b\)

\(c\) \(d\)

对于第二个人，他得到的金币为 \(num*a/d\)。

但如果按下面的顺序排：

\(c\) \(d\)

\(a\) \(b\)

对于第二个人，他得到的金币为 \(num*c/b\)。

此时，就会发现，如果要交换两个人，当且仅当 \(num*a/d<num*c/b\)，把 num 消掉后，经过移项得 \(a*b>c*d\)，所以最佳的选择就是所有数满足 \(a*b<c*d\)。

此题要高精

2. P2123 皇后游戏

link：https://www.luogu.com.cn/problem/P2123

上面那个题得延续吧。思路还是一样的，就是推两个人的关系。

但是因为这个简单的式子没有传递性，所以这样写肯定是不对的。仔细探究这个式子的本质，就是希望前面的数x值越小，y值越大，而且主要是关于这四个数两两的大小关系。分类讨论一下：

\(a[i]<b[i]\), \(a[j]<b[j]\), 按照a值升序排序。
\(a[i]<b[i]\), \(a[j]>b[j]\), 按照 < > 排序。
\(a[i]>b[i]\), \(a[j]<b[j]\), 同2。
\(a[i]>b[i]\), \(a[j]>b[j]\), 按照b值降序排序。

根据这些排序即可。

3. [luogu1248]加工生产调度

和上面那道题没有太大区别，同样的方法，只看两个物品，假设加工他们的时间分别为：

\(a\) \(b\)

\(c\) \(d\)

此时的时间为：\(a+max(b, c)+d\)

但如果按下面的顺序排：

\(c\) \(d\)

\(a\) \(b\)

此时的时间为：\(c+max(d, a)+b\)

就会发现，如果要交换两个物品，当且仅当 \(a+max(b, c)+d>c+max(d, a)+b\)，经过移项得 \(max(b, c)-c-b>max(d, a)-a-d\)，同样得到 \(min(d, a)<max(b, c)\)。

然后就没有然后了。

4. [JXOI2017] 加法

link：https://www.luogu.com.cn/problem/P4064

显然二分。最小值为min，最大值就是min+m*a，问题在于check函数怎么写。

显然是用最优的方法去改变原数组，判断每一位是否大于mid。会发现遍历到 i 位时（i<mid），当前区间能覆盖 l 且 r 的范围更大，那肯定是选当前区间而不选以前选的。所以贪心策略即为优先选择右端点最远的点进行加法。可以用一个大根堆来维护。需要一个支持区间加、单点查的数据结构，肯定是树状数组。注意维护时的合法性（比如选的区间数等）。

check 函数

bool check(int x)
{
	memset(sum, 0, sizeof(sum));
	while(q.size()) q.pop();
	for(int i=1;i<=n;i++)
	{
		add(i, a[i]-a[i-1]);
	}
	int p=1, cnt=0;
	for(int i=1;i<=n;i++)
	{
		while(p<=m&&b[p].l<=i) q.push(b[p++]);
		while(query(i)<x&&!q.empty())
		{
			choce t=q.top();
			q.pop();
			while(!q.empty()&&t.r<i)
			{
				t=q.top();
				q.pop();
			}
			if(t.r<i||++cnt>k) return 0;
			add(t.l, num);
			add(t.r+1, -num);	
		}
		if(query(i)<x) return 0;
	}
	return 1;
}

5. [NOIP2018 提高组] 赛道修建

link：https://www.luogu.com.cn/problem/P5021

~~又是二分，又是不会写判断~~

判断长度最小 \(x\) 是否可行 → \(≥x\) 的段数是否 \(≥m\)

现在只考虑一个点 u 和他所有儿子 v 的情况。用一个 multiset（可自动排序）来记录从每个儿子 v 上来的赛道长度+ u—v 边权。如果儿子两两之间可以配对（每次最小的和与它加起来刚好大于mid的）或单独可以自成一段，那么就删除他们（使得段数更多），个数+1，然后在所有没有删除的值中选一个最大的上传给父亲u，大致就是个dfs。

6. [JOI 2022 Final] 让我们赢得选举

link：https://www.gxyzoj.com/d/hzoj/p/4100?tid=67063ae5f3395ed072f506cd

首先有几个结论：

多个人在同一州演讲比在不同州讲时间短。
肯定是先去协作者+赢得选票（简称合作州）的州再去赢得选票（简称支持州）的州。
去合作州肯定是按b的升序去找的。

剩余的没有获得选票的简称反对州。

发现这个题直接贪心是不可以的，可能一些选中的b对应的a极其地小，此时就不是最优的。所以引入dp。

dp[i][j][k]表示前i个州恰好j个支持州k个合作州的最短时间，因为外面还要枚举协作者的个数，所以复杂度为O(n^4)。考虑化为二维dp，dp[i][j]表示前i个州有j个合作州的最短时间，因为两个合作州之间肯定是支持州（当然算的时候是放到最后），就把支持州的时间带到dp转移里，相当于每一步决策：这一步我是选合作还是支持。感觉特别神奇巧妙，有点说不清楚，感性理解吧。

字符串专项

1. [NOIP2020] 字符串匹配

link：https://www.luogu.com.cn/problem/P7114

好像要用到什么扩展kmp，但貌似只用哈希即可。

考虑一种非常暴力的解法，枚举长度，枚举A，此时就可以知道B，然后暴力判断后面的是否和前面相等。然后加上比C串奇数字符数量小的前面的串的个数，不断add，同树状数组维护桶。代码如下：

点击查看代码

for(int i=1;i<=n;i++)
{
	int l=1, r=i;
	ull tmp=gethash(l, r);
	while(r<=n&&gethash(l, r)==tmp)
	{
		if(r<n) ans+=query(h[r+1]+1);
		l+=i, r+=i;
	}
	add(q[i]+1);
}

Tips：树状数组数组开大点。

2. Short Code

link：https://www.luogu.com.cn/problem/CF965E

考虑建立trie树，问题变为：给一棵树，有一些黑点。可以把黑点移到祖先处，但两个黑点不能在同一个位置。求最小的黑点深度和。

然后给每个节点维护一个大根堆，存这个节点子树内所有黑色节点的深度，往上传的操作可以看成每次将子树内最深的黑色节点放到这个子树的根上，前提是这个根没有黑色节点。最后把根节点所有黑色节点的深度加起来就好了。

3. LG9149. 串串题

link：https://www.luogu.com.cn/problem/P9149

此题比较卡人的点在于这个结论：每个方案数的出现次数之和，等于每个区间可以匹配上的方案数之和。
所以可以分别求每个区间的方案数然后累加。

可以先将A序列除B中出现的数（简称关键字）都放到另一个数组里（显然能匹配上B就不能在完整的匹配中有多余数字）。然后用kmp匹配B，去找到每一个匹配上的区间计算权值。首先算出A原来总共有多少个非关键字（cnt），再算出这个区间原有多少个非关键字（num），我们的目的就是删去这个区间里所有非关键字，区间以外的有没有都无所谓，便可以推出这个贡献：\(C_{cnt-num}^{d-num}\)。然后就没了。

还有比较重要的点就是如何求出这个区间的非关键字数量，因为kmp匹配时是从后往前一遍就过，可以像莫队一样维护两个指针，不断后移即可。

Tips：组合数要非负！！！

4. [CSP-S 2023] 消消乐

link：https://www.luogu.com.cn/problem/P9753

去年CSPs的题，部分分分真的很好拿。一档一档讲吧。

35pts：区间dp，也可以用栈，dp[i][j]表示区间[i,j]是否合法，转移很套路就不说了，然后 O(N^3) 枚举区间记录即可。

50pts：考虑上面的用栈判断一段区间的合法性。有一种常见的优化方式就是只枚举区间的左端点 l ，然后右端点 r 一边扫过去，当栈空的时候所对应的区间 [l,r] 即为合法的一段，每次记录并相加即可。

100pts：真的是出神入化啊。

5. BZOJ1461字符串的匹配

（本来不是专题里面的，是以前觉得太难没有刷过去的）

link：https://www.luogu.com.cn/problem/P6080

这个题真的让我感觉到kmp的精髓了。跟普通kmp的匹配可以说是完全一样、没啥区别的。重要的是你有没有自己想出来。~~答案当然是没有~~

收回上面那句话，此题还是和普通kmp匹配有点区别的（要不然为啥你做不出来）。区别就在于这个排名，可以考虑用树状数组维护一下，首先把b数组的每个数的排名统计一下（相当于我们已经知道前缀的排名），求next的时候只需要关注后缀的排名即可，注意因为有相同的情况，要把每个数＜他的排名也搞出来。

树形dp专项

1.「MXOI Round 1」城市

link：https://www.luogu.com.cn/problem/P9584

我愿称之为：换根dp板子。
这个题看了几眼之后就有思路了，也推出来转移过程（毕竟很板么），但一个巨大的问题就是我的转移顺序是从儿子到父亲的，导致一开始的预处理复杂度很高，不好做。在我几度疑惑中我点开了题解，然后看了第一句话后秒懂，就是说换根板子不太熟练啊。不够敏感。

所以在这里放个板：

点击查看代码

//思路真的完全没有问题但是换根板子不太熟练啊 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+5, mod=998244353;
int n, q, dp[maxn], size[maxn]; 
int f[maxn][20], dis[maxn], dep[maxn], sum;
int t[maxn];
struct edge{
	int next, to, w;
}edge[maxn<<1];
int head[maxn], edgenum;
void add(int from,int to,int w)
{
	edge[++edgenum].next=head[from];
	edge[edgenum].to=to;
	edge[edgenum].w=w;
	head[from]=edgenum;
}
void dfs1(int u,int fa)
{
	size[u]=1;
	for(int i=head[u];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa) continue;
		dis[v]=dis[u]+edge[i].w;
		dfs1(v, u);
		size[u]+=size[v];
	} 
}
void dfs2(int u,int fa)
{
	for(int i=head[u];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa) continue;
		dp[v]=(dp[u]-size[v]*edge[i].w+(n-size[v])*edge[i].w)%mod;
		dfs2(v, u);
	}
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin>>n>>q;
	for(int i=1;i<n;i++)
	{
		int u, v, w;
		cin>>u>>v>>w;
		add(u, v, w);
		add(v, u, w);
	}
	dfs1(1, 0);
	for(int i=1;i<=n;i++) sum+=dis[i];
	dp[1]=sum;
	dfs2(1, 0);
	sum=0;
	for(int i=1;i<=n;i++) sum+=dp[i];
	while(q--)
	{
		int k, w;
		cin>>k>>w;
		cout<<(sum+(dp[k]+w*n)%mod*2)%mod<<"\n";
	}
	return 0;
}

2. Dr. Evil Underscores

link：https://www.luogu.com.cn/problem/CF1285D

看到什么给了很多个数求异或最值，很容易想到01-trie树。然后目标就是找到一条和每一个0/1最接近的路径。

每次到了一个节点u，如果它只有一个儿子，那肯定就直接选这个儿子了；如果它有两个儿子，分别算出两个二子的值（相当于dfs求子树），取更小的那一个 +(1<<当前长度) 。整体是一个自下而上的过程，一步一步往上走。还是比较套路的。这就是所谓的按位贪心。

3. “访问”美术馆

link：https://www.luogu.com.cn/problem/P1270

不是，这个IOI级别的输入啊。递归不断输入即可，~~一般应该不会考这么bt的输入吧？~~

点击查看输入

void dfs(int u)
{
	cin>>x>>y;
	if(y)
	{
		g[u].push_back(make_pair(++idx, x));
		a[idx]=y;
		return ;
	}
	else
	{
		g[u].push_back(make_pair(++idx, x));
		int tmp=idx;
		dfs(tmp);
		dfs(tmp);
	}
}

当然我看了第一篇题解，然后以一种非常奇妙的dp状态转移的，dp[i][j]表示到第i个点，拿了j幅画的最少时间，因为根据题意会发现这个j是有范围的，所以枚举j最大化ans。转移也很好想：\(dp[u][i+j]=min(dp[u][i+j], dp[ls][i]+dp[rs][j]+2*(dis[u][ls]+dis[u][rs]);\)，然后就没啥了。主要就是代码不太好写。

4.「HAOI2015」树上染色

link：https://www.luogu.com.cn/problem/P3177

\(dp[i][j]\) 表示 \(i\) 子树里有 \(j\) 个黑色点，然后只需要枚举当前处理的子树内的黑色节点 (j) 和 i 除了当前子树其他的黑色节点数 (k) 。一条边的贡献就是：\(dp[u][j]+dp[v][k]+k*(K-k)*edge[i].w+(size[v]-k)*(n-(K-k)-size[v])*edge[i].w\)。正常转移，要倒序枚举，避免后效性。

5. Tree Array

link：https://www.luogu.com.cn/problem/CF1540B

苦思冥想了半天也没有想到点上。发现题目里有构造序列、求逆序对这样有连贯性的求贡献的题考虑拆开来算。就比如只算每一个逆序对的贡献。\(dp[i][j]\) 表示第一个数深度为i，第二个数深度为j且\((i, j)\) 为逆序对的概率，因为期望=概率*次数，所以每次只需要枚举根，再枚举逆序对并求和即可。

6. [BalticOI 2021 Day2] The Xana coup

link：https://www.luogu.com.cn/problem/P8127

中间隔了一个题没有写，原因是这几天间歇性自闭，然后颓了。

其实这个题也并不是很难。第一次独立写出代码（虽然看了题解）并一遍AC，好耶✿
经典的决策性问题。

\(f[u][0]\) 表示 u 点目标为0，自身没有操作的最小次数。
\(f[u][1]\) 表示 u 点目标为1，自身没有操作的最小次数。
\(f[u][2]\) 表示 u 点目标为0，自身操作后的最小次数。
\(f[u][3]\) 表示 u 点目标为1，自身操作后的最小次数。

注：以上的操作都只有一次（可以发现对一个点多次取反=一次取反）

转移显然是通过儿子们来的，这个 dp 其实还有一个隐含信息是 u 的子孙节点都为0。
会发现对于一个节点 u ，他的儿子的操作数的奇偶性会影响到自己的决策，所以再开一个数组g来维护儿子们的奇偶性。

\(g[i][0]\) 表示前 i 个儿子都为0，目前总操作数为偶数的最小次数。
\(g[i][1]\) 表示前 i 个儿子都为0，目前总操作数为奇数的最小次数。
\(g[i][2]\) 表示前 i 个儿子都为1，目前总操作数为偶数的最小次数。
\(g[i][3]\) 表示前 i 个儿子都为1，目前总操作数为奇数的最小次数。

然后这个 g 数组的转移就比较简单了，每次只需要在两种组合方式中取min即可（例，偶=偶+偶=奇+奇，奇=偶+奇=奇+偶），f 数组的转移也是非常简单的，需要分类讨论 u 节点为1/0。比较重要的就是需要注意转移完后儿子们必须全为0，细节不多，完。

状压dp专项

1. [USACO13NOV] No Change G

link：https://www.luogu.com.cn/problem/P3092

二分都想到了，一开始状态设计的不对，然后一直想不出来狮子。因为每次转移肯定需要知道上一次转移的位置，所以dp表示此状态能到达的最远距离。转移的时候，枚举i（第几位），当前状态s（第i位为1）的上一个状态就是t（第i位为0，其余与s相同），二分求出从s能到达的最远距离开始，用第i个硬币买完可以到达的最远距离，最后在最远距离到达n的基础上，对剩余钱取max。

第二题是个单调队列，就不放了。

2. [COCI2016-2017#1] Vještica

link：https://www.luogu.com.cn/problem/P6289

小清新状压了吧，首先考虑这个重组字符串相当于只考虑每一个字符的个数，例如s1，s2两个字符串的最长前缀就是对两个字符串中每一个字符的字符数取min后全部加起来。然后这两个字符串的节点数就是 \(|s1|+|s2|-pre+1\)。现在考虑如果是两个字符串集a，b，他们的节点数即为\(dp[a]+dp[b]-pre[a|b]+1\)（dp[s]表示字符串集s的最小节点数），这便是转移方程啦，O(3^n) 枚举子集即可。pre数组预处理出来。

3. New Year Tree

link：https://www.luogu.com.cn/problem/CF620E

爱来自2025/7/17.
我回来写总结了。值得开心的是，时隔半年还是会做这道题，~~虽然没想到最后的统计~~

将树转换为dfs序处理。注意到最多有60种颜色，虽然这样看起来不像状压的数据范围，但我们可以考虑将它存成数，存到线段树的节点里。这样合并一个“|”就过去了。至于答案最后怎么统计，考虑一个叫做lowbit的东西，这样就可以了：

点击查看代码

int ans=0;
for(int i=num;i;i-=lowbit(i)) ans++;

生活似海/起伏不定/无边总是看不到头/我欲乘风/浪迹远方/因为我并不平凡普通

posted @ 2024-08-24 17:59 zhouyiran2011 阅读(122) 评论(2) 收藏举报

刷新页面返回顶部

zhouyiran2011

专项训练1

数据结构专题

1. [SNOI2017]一个简单的询问

2. [USACO19DEC] Bessie's Snow Cow P

3. [十二省联考 2019] 春节十二响

4. [SDOI2011] 消防

5. [HNOI2016] 序列

数论专题

1. [ABC281G] Farthest City

2. [ABC305G] Banned Substrings

3. [CQOI2016] 密钥破解

4. [NOI2018] 屠龙勇士

5.「雅礼集训 2018 Day10」足球大战

DP杂项

1. [PA2021] Od deski do deski

2. [TJOI2019] 甲苯先生的字符串

3. [ABC213G] Connectivity 2

DP专题

1. [NOIP2021] 数列

2. [ABC234G] Divide a Sequence

3. [春季测试 2023] 圣诞树

图论专题

1. 小L的有向图

2.「NOIP2017」逛公园

3. [bzoj2438] [中山市选2011]杀人游戏

图论杂项

1.「NOIP2013」华容道

2. Star Way To Heaven

3. Berland and the Shortest Paths

贪心专项

1.「NOIP2012」国王游戏

2. P2123 皇后游戏

3. [luogu1248]加工生产调度

4. [JXOI2017] 加法

5. [NOIP2018 提高组] 赛道修建

6. [JOI 2022 Final] 让我们赢得选举

字符串专项

1. [NOIP2020] 字符串匹配

2. Short Code

3. LG9149. 串串题

4. [CSP-S 2023] 消消乐

5. BZOJ1461字符串的匹配

树形dp专项

1.「MXOI Round 1」城市

2. Dr. Evil Underscores

3. “访问”美术馆

4.「HAOI2015」树上染色

5. Tree Array

6. [BalticOI 2021 Day2] The Xana coup

状压dp专项

1. [USACO13NOV] No Change G

2. [COCI2016-2017#1] Vještica

3. New Year Tree

公告