Diffusion model笔记
Denoising Diffusion Probabilistic Models 去噪扩散概率模型
只是笔记没有原创性内容
来自博客:https://zaixiang.notion.site/Diffusion-Models-for-Deep-Generative-Learning-24ccc2e2a11e40699723b277a7ebdd64#4676714d938945c99c394f00cf6e4e91
前置知识
1 负对数似然(negative log-likehood, NLL)
1)似然
似然与概率不同。概率是指一个事件发生的可能性,描述的是对象是事件;似然是指影响事件发生概率的未知参数,描述的对象是参数。由于参数有一定的值(虽然未知),并非事件或随机变量,无概率可言,于是改用“似然”一词。
假设是离散随机变量,其概率质量函数\(p\)依赖于参数\(\theta\),则:
其中,\(L(\theta \mid X)\)为参数\(\theta\)的似然函数,\(x\)为随机变量\(X\)的某一值。
2)最大似然估计
最大似然估计(Maximum Likehood Estimation, MLE)是参数估计的一种方法,其估计的对象是参数。
假设我们有一个非常复杂的数据分布\(P_{data}(x)\),但我们不知道该分布的数学表达形式,所以我们需要定义一个分布模型\(P_G(x;\theta)\)(这里的分布模型我们事先是知道的,如正态分布、均匀分布等),该分布由参数\(\theta\)决定。
我们的目标就是求得参数\(\theta\),使得定义的分布\(P_G(x;\theta)\)尽可能地接近\(P_{data}(x)\)。
通过以下步骤来进行最大似然估计:
1.从\(P_{data}(x)\)中采集\(m\)个样本:\(x_1\),\(x_2\),...,\(x_m\);
2.计算样本的似然函数\(L=\prod_{t=1}^T {P_G(x^i;\theta)}\),其中,\(\prod\)为求积符号;
3.求使得似然函数\(L\)最大的参数\(\theta\):
当来自\(P_{data}(x)\)的样本:\(x_1\),\(x_2\),...,\(x_m\)在\(P_G(x;\theta)\)分布模型中出现的概率越高,即\(\prod_{t=1}^T {P_G(x^i;\theta)}\)越大时,\(P_G(x;\theta)\)和\(P_{data}(x)\)越接近。
在“模型已定,参数未知”的情况下,使用最大似然估计算法学习参数是比较普遍的。
3)对数似然
似然函数\(\prod_{t=1}^T {P_G(x^i;\theta)}\)取对数,即得到对数似然(log-likehood)。
对数似然公式表示为:
这样,就对\(\theta\)求解的问题就转化为了求极值的经典问题。解决思路为:“求偏导\(\rightarrow\)令偏导等于零\(\rightarrow\)求得参数”。
4)负对数似然
顾名思义,负对数似然(negative log-likehood)即是对对数似然取负。由于概率分布\(P_G \left ( x;\theta \right )\)取值为\([0,1]\) ,取对数后,取值为\([0,-\infty]\);再取符号,取值变为\([0,+\infty]\),如下图所示:
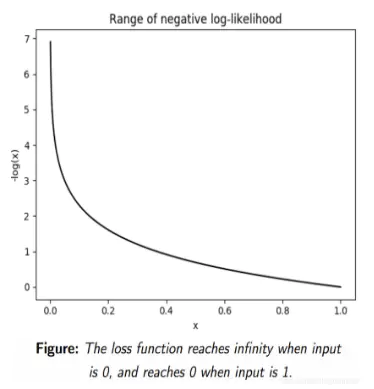
负对数似然公式表示为:
实际中,\(P_G(x^i;\theta)\)为概率值。
注:交叉熵公式为:
其中\(p\)为真实概率分布,\(q\)为预测概率分布。实际中,由于真实标签中,除了对应类别外,其他概率都为0,因此\(p(x_i)=1\)。
故交叉熵可简写为:
可以明显看出,负对数似然和交叉熵有高度的相似性。其实,在分类问题中,所使用的的交叉熵损失,本质就是负对数似然。
实际中,我们希望最大化似然估计,以得到最接近数据分布的模型,即希望\(\sum_{i=1}^{m}\left ( P_G\left ( x^i;\theta \right ) \right )\)最大,那么也即最\(-\sum_{i=1}^{m}\left ( P_G\left ( x^i;\theta \right ) \right )\)小。此外,由上图也可以看出,当负对数似然函数的输入(概率)越接近于1时,函数值越接近于0。因此,可将负对数似然作为损失函数。
5) 补充说明
负对数似然损失函数在Pytorch中对应函数\({\color{Red} torch.nn.NLLLoss\left ( \right )}\)。
需要指出的是,虽然Pytorch的\(nn.LLLoss()\)名为负对数似然,但其内部并没有进行对数计算,而是仅仅求和平均后取负(函数参数reduction为默认值'mean',参数weight为默认值'none'时)。所以实际使用中,需将\(nn.LLLoss()\)与 \({\color{Red} torch.nn.LogSoftmax\left ( \right )}\)一起使用,即先对数据进行\(logsoftmax()\)处理后,再输入\(nn.LLLoss()\)中,才能得到负对数似然损失。或者,直接使用交叉熵损失函数:\({\color{Red} torch.nn.CrossEntropyLoss\left ( \right )}\)。
以下代码说明了这一点:
>>> import torch.nn as nn
>>> m = nn.LogSoftmax(dim=1)
>>> Loss_NLLL = nn.NLLLoss()
>>> # input is of size N x C = 3 x 5
>>> input = torch.randn(3, 5, requires_grad=True)
>>> input_LS = m(input)
>>> # each element in target has to have 0 <= value < C
>>> target = torch.tensor([1, 0, 4])
>>> input
tensor([[-0.2512, 0.7716, -0.1233, -0.9330, 1.1369],
[ 0.0206, -0.0298, 0.0595, -0.2068, 0.2119],
[ 0.6677, -1.6576, -0.7711, -0.2504, -0.2911]], requires_grad=True)
>>> input_LS
tensor([[-2.2439, -1.2211, -2.1160, -2.9258, -0.8559],
[-1.6090, -1.6594, -1.5701, -1.8364, -1.4177],
[-0.7503, -3.0756, -2.1891, -1.6684, -1.7091]],
grad_fn=<LogSoftmaxBackward0>)
>>> #交叉熵损失
>>> Loss_CE = nn.CrossEntropyLoss()
>>> loss_NLLL = Loss_NLLL(input, target) #未加LogSoftmax()的负对数损失
>>> loss_NLLL_LS = Loss_NLLL(input_LS, target) #加了LogSfotmax()的负对数损失
>>> loss_CE = Loss_CE(input, target) #交叉熵损失
>>> loss_NLLL
tensor(-0.1670, grad_fn=<NllLossBackward0>)
>>> loss_NLLL_LS
tensor(1.5131, grad_fn=<NllLossBackward0>)
>>> loss_CE
tensor(1.5131, grad_fn=<NllLossBackward0>)
从以上代码示例可以看到,loss_NLLL_LS = loss_CE,即,加了LogSoftmax的NLLLoss所得结果和CrossEntropyLoss结果相同。
2 贝叶斯公式
若满足马尔科夫链关系$A\rightarrow B\rightarrow C $,即当前时刻的概率分布仅与上一时刻有关,则有:
下文中公式(7-1)推导过程:
2 高斯分布的概率密度函数、高斯函数的叠加公式
给定均值为\(\mu\),方差为 \(\sigma ^{2}\) 的单一变量高斯分布 \(\mathcal{N}(\mu , \sigma ^{2})\),其概率密度函数为:
很多时候,为了方便起见,可以将前面的常数系数去掉,写成:
给定两个高斯分布 \(X\sim \mathcal{N}(\mu_{1} , \sigma_{1} ^{2})\),\(Y\sim \mathcal{N}(\mu_{2} , \sigma_{2} ^{2})\),则它们叠加后的分布\(aX+bY\) 满足:
3 KL散度与交叉熵
期望公式:
假设随机变量的真实概率分布为 \(P\),而我们通过建模得到的一个近似分布为 \(Q\),则 \(P\)与\(Q\)的KL散度和交叉熵满足下式:
对于两个单一变量的高斯分布 \(p\sim \mathcal{N}(\mu _{1}, \sigma _{1}^{2})\) 和\(q\sim \mathcal{N}(\mu _{2}, \sigma _{2}^{2})\) 而言,它们的KL散度为:
4 重参数(reparameterization trick)
理解方式1:
重参数技巧在很多工作(gumbel softmax, VAE)中有所引用。如果我们要从某个分布中随机采样(高斯分布)一个样本,这个过程是无法反传梯度的。而这个通过高斯噪声采样得到 \(x_t\) 的过程在diffusion中到处都是,因此我们需要通过重参数技巧来使得他可微。最通常的做法是把随机性通过一个独立的随机变量( \(\epsilon\))引导过去。举个例子,如果要从高斯分布\(z\sim \mathcal{N}(z;\mu_\theta,\sigma_\theta^2\mathbf{I})\) 采样一个\(z\),我们可以写成:
上式的\(z\)依旧是有随机性的, 且满足均值为\(\mu_\theta\) 方差为\(\sigma_\theta^{2}\)的高斯分布。这里的\(\mu_\theta\) ,\(\sigma_\theta^{2}\)可以是由参数\(\theta\) 的神经网络推断得到的。整个“采样”过程依旧梯度可导,随机性被转嫁到了 \(\epsilon\)上。
理解方式2:
若要从高斯分布 \(\mathcal{N}(\mu ,\sigma^{2} )\) 中采样,可先从标准分布 \(\mathcal{N}(0 ,1 )\) 中采样出 \(z\),再得到 \(\sigma ^{2}\ast z + \mu\),即我们的采样值。这样做的目的是将随机性转移到 \(z\) 上,让采样值对 \(\mu\) 和 \(\sigma\) 可导。(仅提取随机性)
正文
diffusion model和其他模型最大的区别是它的latent code(z)和原图是同尺寸大小的,当然最近也有基于压缩的latent diffusion model[5],不过是后话了。一句话概括diffusion model,即存在一系列高斯噪声( \(T\) 轮),将输入图片 \(x_0\)变为纯高斯噪声 \(x_T\)。而我们的模型则负责将 \(x_T\)复原回图片 \(x_0\)。这样一来其实diffusion model和GAN很像,都是给定噪声 \(x_T\)生成图片\(x_0\) ,但是要强调的是,这里噪声 \(x_T\)与图片\(x_0\)是同维度的。
Diffusion前向过程
所谓前向过程,即往图片上加噪声的过程。虽然这个步骤无法做到图片生成,但是这是理解diffusion model以及构建训练样本GT至关重要的一步。
给定真实图片$ x_0\sim q(x)$,diffusion前向过程通过 \(T\) 次累计对其添加高斯噪声,得到 \(x_1,x_2,...,x_T\),如下图的\(q\)过程。这里需要给定一系列的高斯分布方差的超参数 \(\{\beta_t\in(0,1)\}_{t=1}^{T}\).前向过程由于每个时刻 \(t\) 只与 \(t−1\) 时刻有关,所以也可以看做马尔科夫过程:
这个过程中,随着\(t\) 的增大, \(x_t\) 越来越接近纯噪声。当\(T\rightarrow\infty\), \(x_T\) 是完全的高斯噪声(下面会证明,且与均值系数\(1−β_t\) 的选择有关)。且实际中 \(β_t\) 随着\(t\)增大是递增的,即 \(\beta_1<\beta_2<...<\beta_T。\)在GLIDE的code中, \(β_t\) 是由0.0001 到0.02线性插值(以 \(T\)=1000 为基准, \(T\) 增加, \(β_t\) 对应降低)。

任意时刻的 \(x_t\) 可以由 \(x_0\) 和 \(\beta\) 表示
能够通过 \(x_0\) 和 \(\beta\) 快速得到\(x_t\)对后续diffusion model的推断和推导有巨大作用。首先我们假设$\alpha_t=1-\beta_t $ ,并且\(\overline{\alpha}_t=\prod_{i=1}^{T}\alpha_i\),展开 \(x_t\) 可以得到:
由于独立高斯分布可加性,即\(\mathcal{N}(0,\sigma_1^2\mathbf{I})+\mathcal{N}(0,\sigma_2^2\mathbf{I})\sim\mathcal{N}(0,(\sigma_1^2+\sigma_2^2)\mathbf{I})\),所以
因此可以混合两个高斯分布得到标准差为 \(\sqrt{1-\alpha_t \alpha_{t-1}}\)的混合高斯分布,然而Eq(3)中的\(\overline{z}_{2}仍\)然是标准高斯分布。而任意时刻的 \(x_t\) 满足\(q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\overline{\alpha}_t}x_0, (1-\overline{\alpha}_t)\mathbf{I})\).
一开始笔者一直不清楚为什么Eq(1)中diffusion的均值每次要乘上 $ \sqrt{1-\beta_t}$.明明 \(\beta_t\)只是方差系数,怎么会影响均值呢?替换为任何一个新的超参数,保证它<1,也能够保证值域并且使得最后均值收敛到0(但是方差并不为1). 然而通过Eq(3)(4),可以发现当\(T\rightarrow\infty\), \(x_T\sim\mathcal{N}(0,\mathbf{I})\) 所以\(\sqrt{1−\beta_t}\)的均值系数能够稳定保证 \(x_T\) 最后收敛到方差为1的标准高斯分布,且在Eq(4)的推导中也更为简洁优雅。(个人感觉比较直观的是推导变简单了,还有没有其他作用正在学习中)
Diffusion逆向(推断)过程
如果说前向过程(forward)是加噪的过程,那么逆向过程(reverse)就是diffusion的去噪推断过程。如果我们能够逐步得到逆转后的分布 \(q(x_{t−1}|x_t)\) ,就可以从完全的标准高斯分布 $x_T∼\mathcal{N}(0,\mathbf{I}) $还原出原图分布 \(x_0\) .在文献[7]中证明了如果 \(q(x_t|x_{t−1})\) 满足高斯分布且 \(β_t\) 足够小,\(q(x_{t−1}|x_t)\)仍然是一个高斯分布。然而我们无法简单推断\(q(x_{t−1}|x_t)\),因此我们使用深度学习模型(参数为 \(\theta\) ,目前主流是U-Net+attention的结构)去预测这样的一个逆向的分布 \(p_\theta\)(类似VAE) :
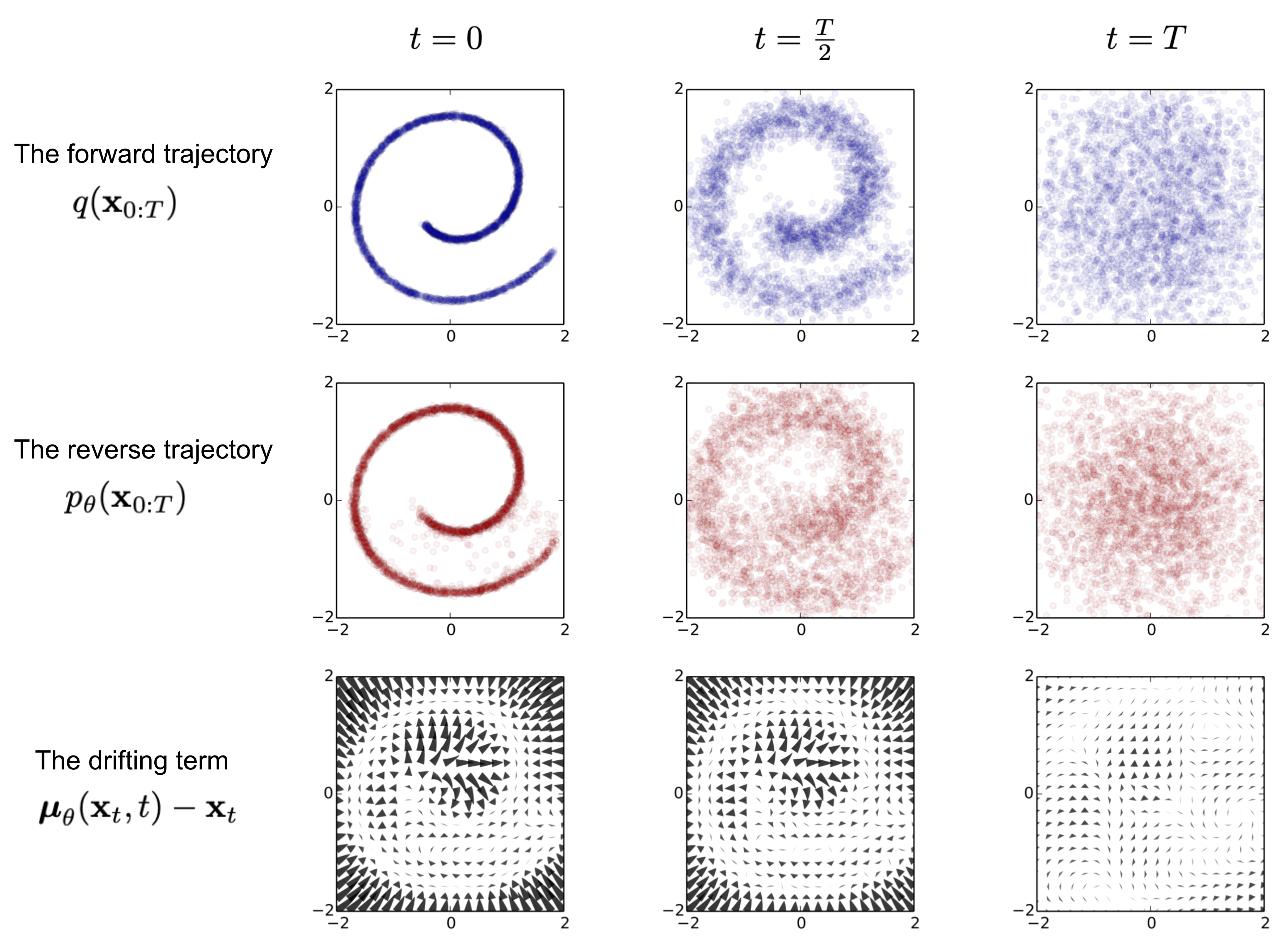
虽然我们无法得到逆转后的分布 \(q(x_{t−1}|x_t)\),但是如果知道 \(x_0\) ,是可以通过贝叶斯公式得到 \(q(x_{t−1}|x_t,x_0)\) 为:
过程如下:
我们的目标是从\(x_T\)得到一张尽可能真实的图像\(x_0\),但也不能一蹴而就,需要一步一步从$ x_t\rightarrow x_{t-1}$,由贝叶斯公式可得:
由于马尔科夫链的性质,可以加上条件\(x_0\),即:(也可以按照文章一开头的贝叶斯公式推导得到)
上式巧妙地将逆向过程全部变回了前向,即给定\(x_t\)和\(x_0\),我们是可以计算出\(x_{t-1}\) ,分别写出其对应的高斯概率密度函数。一般的高斯概率密度函数的指数部分应该写为 \(\exp\Big({-\frac{(x-\mu)^2}{2\sigma^2}}\Big)=\exp\Big(-\frac{1}{2}(\frac{1}{\sigma^2}x^2-\frac{2\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2})\Big)\),因此稍加整理我们可以得到(6)中的方差和均值为:
前向过程中有 \(x_0=\frac{1}{\sqrt{\overline{\alpha}_t}}(x_t-\sqrt{1-\overline{\alpha}_t}\overline{z}_t)\),带入(8-2)可以得到
其中高斯分布\(\overline{z}_t\) 为深度模型所预测的噪声(用于去噪),可看做为 \(z_θ(x_t,t)\) ,即得到:
所以,在给定 \(x_{0}\)的条件下,反向过程真实的概率分布的均值只与 \(x_{t}\) 和\(\bar{z}_{t}\) 有关,满足下式:
这样一来,DDPM的每一步的推断可以总结为:
1) 每个时间步通过 \(x_t\) 和\(t\) 来预测高斯噪声\(z_θ(x_t,t)\),随后根据(9)得到均值\(\mu_\theta(x_t,t)\).
2)得到方差\(\Sigma_\theta(x_t,t)\),DDPM中使用untrained \(\Sigma_\theta(x_t,t)=\tilde{\beta}_t\)且认为 \(\tilde{\beta}_t =\beta_t\)和 \(\tilde{\beta}_t=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_t}\cdot\beta_t\)结果近似,在GLIDE中则是根据网络预测trainable方差 \(\Sigma_\theta(x_t,t)\).
3) 根据(5-2)得到 \(q(x_{t−1}|x_t)\) ,利用重参数得到 $x_{t−1} $.
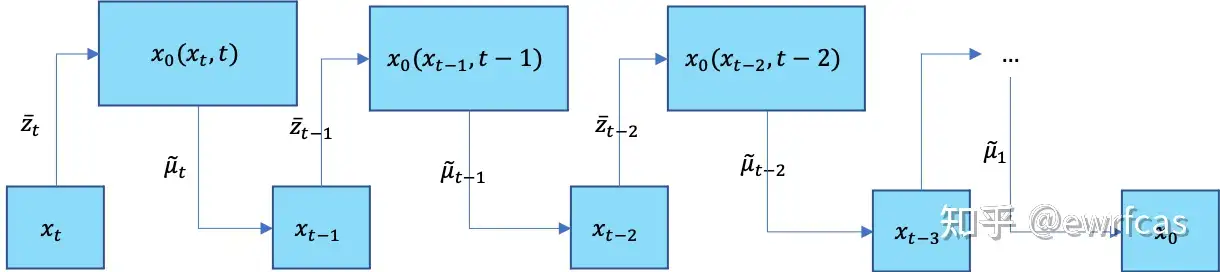
Diffusion训练
如何训练diffusion model以得到靠谱的\(μ_θ(x_t,t)\)和\(\sum_θ(x_t,t)\)呢?通过对真实数据分布下,最大化模型预测分布的对数似然,即优化在$ x_0∼q(x_0)$ 下的 \(p_θ(x_0)\) 交叉熵:
我们可以在负对数似然函数的基础上加上一个KL散度,于是就构成了负对数似然的上界了,上界越小,负对数似然自然也就越小,那么对数似然就越大了。
对(11)左右取期望\(\mathbb{E}_{q(x_0)}\),利用到重积分中的Fubini定理:
能够最小化\(\mathcal{L}_{VLB}\)即可最小化我们的目标损失(10)。
另一方面,通过Jensen不等式也可以得到一样的目标:
进一步对\(\mathcal{L}_{VLB}\)推导,可以得到熵与多个KL散度的累加,具体可见文献[8]。
也可写为:
由于前向 \(q\) 没有可学习参数,而$ x_T$则是纯高斯噪声, \(L_T\) 可以当做常量忽略。而 \(L_t\) 则可以看做拉近2个高斯分布 \(q(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};\tilde{\mu}(x_t,x_0),\tilde{\beta_t}\mathbf{I})\)和 $p_\theta(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta) $,根据多元高斯分布的KL散度求解:
其中\(C\)是与模型参数 \(θ\) 无关的常量。把(8-3)的\(\tilde{\mu}_t(x_t,x_0)(9\))的 \(μ_θ(x_t,t)\) 和(3)的 \(x_t\) 带入(15)可以得到:
从(16)可以看出,diffusion训练的核心就是取学习高斯噪声 \(\overline{z}_t\) , \(z_θ\) 之间的MSE。
$L_0=−logp_θ(x_0|x_1) $相当于最后一步的熵,DDPM论文指出,从 \(x_1\) 到 \(x_0\) 应该是一个离散化过程,因为图像RGB值都是离散化的。DDPM针对 \(p_θ(x_0|x_1)\) 构建了一个离散化的分段积分累乘,有点类似基于分类目标的自回归(auto-regressive)学习。有兴趣的同学可以去参考原文。
DDPM将loss进一步简化为:
正如之前提过的,DDPM并没有将模型预测的方差 \(Σ_θ(x_t,t)\) 考虑到训练和推断中,而是通过untrained \(β_t\) 或者(8-1) \(\tilde{\beta}_t\)代替。他们发现 \(Σ_θ\) 可能导致训练的不稳定。
训练过程可以看做:
1)获取输入 \(x_0\) ,从 \(1...T\) 随机采样一个 \(t\) .
2) 从标准高斯分布采样一个噪声 \(\overline{z}_t\sim\mathcal{N}(0,\mathbf{I})\) .
3) 最小化\(||\overline{z}_t-z_\theta(\sqrt{\overline{\alpha}_t}x_0+\sqrt{1-\overline{\alpha}_t}\overline{z}_t,t)||\).
最后再附上DDPM提供的训练/测试(采样)流程图

加速Diffusion采样和方差的选择(DDIM)
DDPM的高质量生成依赖于较大的$ T$ (一般为1000或以上),这就导致diffusion的前向过程非常缓慢。在denoising diffusion implicit model (DDIM)[9]中提出了一种牺牲多样性来换取更快推断的手段。
根据独立高斯分布可加性,我们可以得到 \(x_{t−1}\) 为:
不同于(6)和(9),(18)将方差 \(σ_t^2\) 引入到了均值中,当\(\sigma_t^2=\tilde{\beta}_t=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_t}\beta_t\)时,(18)等价于(6)。
在DDIM中吧由(18)经过贝叶斯得到的 \(q_\sigma(x_t|x_{t-1},x_0)\) 称为非马尔科夫过程,因为 \(x_t\) 的概率同时依赖于 \(x_{t−1}\) 和 \(x_0\) 。(笔者并不了解刻意强调这个非马尔科夫是原因,也许是为了使得(18)中方差出现在均值合理化?)DDIM进一步定义了 \(\sigma_t(\eta)^2=\eta\cdot\tilde{\beta}_t\).当 $η=0 $时,diffusion的sample过程会丧失所有随机性从而得到一个deterministic的结果(但是可以改变 \(x_T\) )。而 \(η=1\) 则DDIM等价于DDPM(使用\(\tilde{\beta}_t\)作为方差的版本).用随机性换取生成性能的类似操作在GAN中也可以通过对latent code操作实现。
对于方差 \(σ_t^2\) 的选择,我们在这里重新整理一下
DDPM:
1) \(\sigma_{t,\theta}^2=\Sigma_\theta(x_t,t)\)相当于模型学习的方差,DDPM称为learned,实际没有使用(但是GLIDE使用的是这种方差)。
2) \(\sigma_{t,s}^2=\tilde{\beta}_t=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_t}\beta_t\),由(8-1)得到,DDPM称为fixedsmall,用于celebahq和lsun。
3) \(\sigma_{t,l}^2=\beta_t\),DDPM称为fixedlarge,用于cifar10,注意 \(\sigma_{t,l}>\sigma_{t,s}\) ,fixedlarge的方差大于fixedsmall的。
DDIM:
\(\sigma_t(\eta)^2=\eta\cdot\tilde{\beta}_t\),DDIM所选择的是基于fixedsmall版本上再乘以一个 \(η\) .
假设总的采样步 \(T=1000\) ,间隔是 \(Q\) ,DDIM采样的步数为 \(S=T/Q\) ,\(S\) 和$ η$ 的实验结果如下:
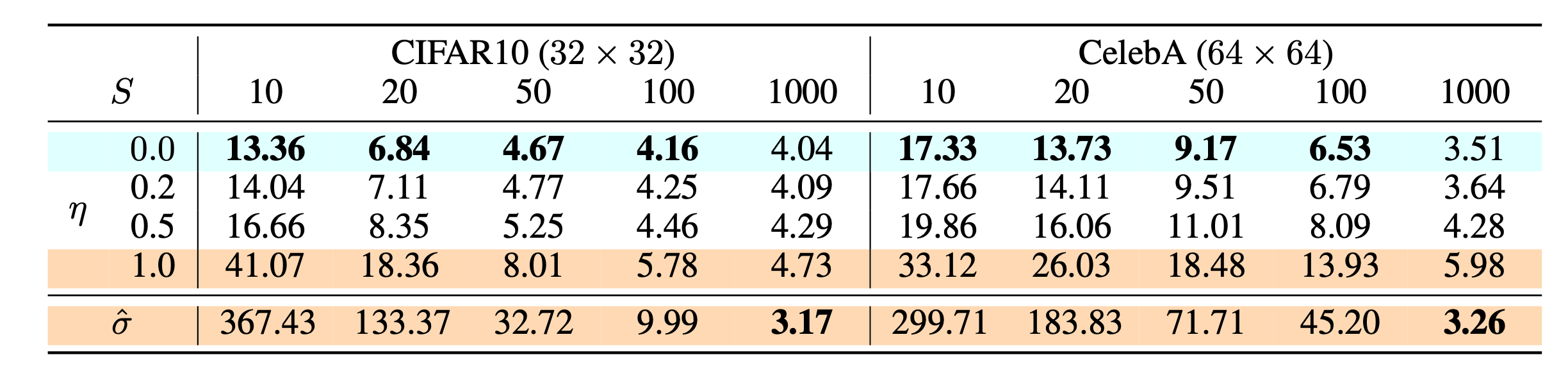
可以发现在 \(S\) 很小的时候 \(η=0\) 取得了最好的结果。值得一提的是, \(η=1\) 是等价于DDPM的fixedsmall版本。而 \(\hat{\sigma}=\sqrt{\beta_t}\)表示的是DDPM的fixedlarge版本。因此当 \(T\) 足够大的时候使用更大的方差 \(σ_t^2\) 能取得更好的结果。
参考
- ^https://lilianweng.github.io/posts/2021-07-11-diffusion-models
- ^Nichol, Alex, et al. "Glide: Towards photorealistic image generation and editing with text-guided diffusion models." arXiv preprint arXiv:2112.10741 (2021).
- ^Ramesh, Aditya, et al. "Hierarchical text-conditional image generation with clip latents." arXiv preprint arXiv:2204.06125 (2022).
- ^Saharia, Chitwan, et al. "Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding." arXiv preprint arXiv:2205.11487 (2022).
- ^Rombach, Robin, et al. "High-Resolution Image Synthesis with Latent Diffusion Models." arXiv preprint arXiv:2112.10752 (2021).
- ^Ho, Jonathan, Ajay Jain, and Pieter Abbeel. "Denoising diffusion probabilistic models." Advances in Neural Information Processing Systems 33 (2020): 6840-6851.
- ^Feller, William. "On the theory of stochastic processes, with particular reference to applications." Proceedings of the [First] Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, 1949.
- ^Sohl-Dickstein, Jascha, et al. "Deep unsupervised learning using nonequilibrium thermodynamics." International Conference on Machine Learning. PMLR, 2015.
- ^Song, Jiaming, Chenlin Meng, and Stefano Ermon. "Denoising diffusion implicit models." arXiv preprint arXiv:2010.02502 (2020).
'''
@file: DDPM.py
@author: silvan
@time: 2023/1/6 17:22
'''
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_s_curve
import torch
##############################1 准备S曲线#####################################################
s_curve,_ = make_s_curve(10**4,noise=0.1) #生成10000个点,方差为0.1
s_curve = s_curve[:,[0,2]]/10.0 #每个点只取第0维和第2维,s_curve的形状是[10000, 2]
# print("shape of moons:",np.shape(s_curve))
data = s_curve.T
fig,ax = plt.subplots()
ax.scatter(*data,color='red',edgecolor='white');
ax.axis('off')
# plt.show()
plt.close()
dataset = torch.Tensor(s_curve).float() #把它构建成一个张量,变成float类型,作为训练集
##############################2 确定超参数的值#######################################################
num_steps = 100 #确定超参数的值,步骤设为100
#制定每一步的beta,sigmoid函数递增
betas = torch.linspace(-6,6,num_steps) #-6到6之间取100个数,包括两个端点
betas = torch.sigmoid(betas)*(0.5e-2 - 1e-5)+1e-5 #先压缩到 0~1 再乘以 0.005,最终\beta为0-1之间很小的数,最大值为0.5e-2,最小值为1e-5
#计算alpha、alpha_prod、alpha_prod_previous、alpha_bar_sqrt等变量的值
alphas = 1-betas
alphas_prod = torch.cumprod(alphas,0) #α_prod是把整个α连乘
alphas_prod_p = torch.cat([torch.tensor([1]).float(),alphas_prod[:-1]],0)#α_prod_previous只取α_prod的第一项开始,第0项设为1
alphas_bar_sqrt = torch.sqrt(alphas_prod)#α_bar_sqrt是α_prod的开根号
one_minus_alphas_bar_log = torch.log(1 - alphas_prod)#一减去α bar log
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)#一减去α bar sqrt
#所有参数形状大小都是一样的[100],这些值是超参数,不需要训练的
# assert alphas.shape==alphas_prod.shape==alphas_prod_p.shape==\
# alphas_bar_sqrt.shape==one_minus_alphas_bar_log.shape==one_minus_alphas_bar_sqrt.shape
# print("all the same shape",betas.shape)
###############################3 确定扩散过程任意时刻的采样值###############################################
'''确定扩散过程任意时刻的采样值
计算q(xt|x0)公式,给定初始的训练数据分布,算出任意时刻xt的采样值
公式只和x0和t有关,首先生成正态分布的随机 噪声noise,得到均值和方差,使用重参数技巧,噪声乘以标准差alphas_1_m_t,加上一个均值alphas_t * x_0
'''
# 计算任意时刻的x采样值,基于x_0和重参数化
def q_x(x_0, t):
"""可以基于x[0]得到任意时刻t的x[t]"""
noise = torch.randn_like(x_0)
alphas_t = alphas_bar_sqrt[t]
alphas_1_m_t = one_minus_alphas_bar_sqrt[t]
return (alphas_t * x_0 + alphas_1_m_t * noise) # 在x[0]的基础上添加噪声
##################################4 演示原始数据分布加噪100步后的结果########################################
'''
演示原始数据加噪100步,每间隔5步画出共20张图,遍历循环,传入一个时刻t,传入qx函数中算出x5的值,将图片画出来
'''
num_shows = 20
fig,axs = plt.subplots(2,10,figsize=(28,3))
plt.rc('text',color='black')
#共有10000个点,每个点包含两个坐标
#生成100步以内每隔5步加噪声后的图像
#num_steps=100
for i in range(num_shows):
# 在Python中“/”表示浮点数除法,返回浮点结果,也就是结果为浮点数,
# 而“//”在Python中表示整数除法,返回不大于结果的一个最大的整数,意思就是除法结果向下取整。
j = i//10
k = i%10
q_i = q_x(dataset,torch.tensor([i*num_steps//num_shows]))#生成t时刻的采样数据
axs[j,k].scatter(q_i[:,0],q_i[:,1],color='red',edgecolor='white')
axs[j,k].set_axis_off()
axs[j,k].set_title('$q(\mathbf{x}_{'+str(i*num_steps//num_shows)+'})$')
# plt.show()
plt.close()
################################5、编写拟合逆扩散过程高斯分布的模型#########################################
'''
编写拟合逆扩散过程高斯分布的模型
模型对应εθ网络
输入的t经过embedding层,将x输入linear层和relu,输出的结果加上t_embedding,再送入relu层,
每一层的embedding都是新的一个可学习的embbedding,最后输出x。
十分简单的网络,完全由MLP和Relu构成
'''
import torch
import torch.nn as nn
class MLPDiffusion(nn.Module):
def __init__(self, n_steps, num_units=128):
super(MLPDiffusion, self).__init__()
self.linears = nn.ModuleList(
[
nn.Linear(2, num_units),
nn.ReLU(),
nn.Linear(num_units, num_units),
nn.ReLU(),
nn.Linear(num_units, num_units),
nn.ReLU(),
nn.Linear(num_units, 2),
]
)
self.step_embeddings = nn.ModuleList(
[
nn.Embedding(n_steps, num_units),
nn.Embedding(n_steps, num_units),
nn.Embedding(n_steps, num_units),
]
)
def forward(self, x, t):
# x = x_0
for idx, embedding_layer in enumerate(self.step_embeddings):
t_embedding = embedding_layer(t)
x = self.linears[2 * idx](x)
x += t_embedding
x = self.linears[2 * idx + 1](x)
x = self.linears[-1](x)
return x
####################6、编写训练的误差函数 ###########################################
'''
最简单的就是ε-εθ的MSE
对batchsize样本随机生成时刻t,t随机分散,先生成一半,另一半的t=n_steps-1-t,起到t尽量不重复的效果
t的形状[batchsize,1],将1维度压缩掉,unsqueeze,方便我们取系数
生成噪声ε,根据均值和标准差缩放平移成model输入x,再将t输入得到输出
和噪声ε做MSE得到loss
'''
def diffusion_loss_fn(model, x_0, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, n_steps):
"""对任意时刻t进行采样计算loss"""
batch_size = x_0.shape[0]
# 对一个batchsize样本生成随机的时刻t
t = torch.randint(0, n_steps, size=(batch_size // 2,))
t = torch.cat([t, n_steps - 1 - t], dim=0)
t = t.unsqueeze(-1)
# x0的系数
a = alphas_bar_sqrt[t]
# eps的系数
aml = one_minus_alphas_bar_sqrt[t]
# 生成随机噪音eps
e = torch.randn_like(x_0)
# 构造模型的输入
x = x_0 * a + e * aml
# 送入模型,得到t时刻的随机噪声预测值
output = model(x, t.squeeze(-1))
# 与真实噪声一起计算误差,求平均值
return (e - output).square().mean()
####################7、编写逆扩散采样函数(inference)###################################
'''
逆扩散采样
p sample loop从xt中恢复 xt-1,xt-2,…, x0
p sample就是一个参数重整化的过程,根据μθ公式得到均值,方差是βt的开方
在生成正态分布的随机量z,z乘上方差加上均值得到sample
'''
def p_sample_loop(model, shape, n_steps, betas, one_minus_alphas_bar_sqrt):
"""从x[T]恢复x[T-1]、x[T-2]|...x[0]"""
cur_x = torch.randn(shape)
x_seq = [cur_x]
for i in reversed(range(n_steps)):
cur_x = p_sample(model, cur_x, i, betas, one_minus_alphas_bar_sqrt)
x_seq.append(cur_x)
return x_seq
def p_sample(model, x, t, betas, one_minus_alphas_bar_sqrt):
"""从x[T]采样t时刻的重构值"""
t = torch.tensor([t])
coeff = betas[t] / one_minus_alphas_bar_sqrt[t]
eps_theta = model(x, t)
mean = (1 / (1 - betas[t]).sqrt()) * (x - (coeff * eps_theta))
z = torch.randn_like(x)
sigma_t = betas[t].sqrt()
sample = mean + sigma_t * z
return (sample)
############################8、开始训练模型,打印loss及中间重构效果##########################
'''
编写训练代码
构造dataloader,遍历epoch次,遍历dataloader数据集
计算loss,送入optimizer进行优化
'''
seed = 1234
class EMA():
"""构建一个参数平滑器"""
def __init__(self, mu=0.01):
self.mu = mu
self.shadow = {}
def register(self, name, val):
self.shadow[name] = val.clone()
def __call__(self, name, x):
assert name in self.shadow
new_average = self.mu * x + (1.0 - self.mu) * self.shadow[name]
self.shadow[name] = new_average.clone()
return new_average
print('Training model...')
batch_size = 128
# 将自定义的dataset根据batch size的大小、是否shuffle等选项封装成一个batch size大小的tensor,
# 后续就只需要再包装成variable即可作为模型的输入进行训练
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)
num_epoch = 4000
plt.rc('text', color='blue')
model = MLPDiffusion(num_steps) # 输出维度是2,输入是x和step
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
for t in range(num_epoch):
for idx, batch_x in enumerate(dataloader):
loss = diffusion_loss_fn(model, batch_x, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, num_steps)
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.)
optimizer.step()
if (t % 1000 == 0):
print(loss)
x_seq = p_sample_loop(model, dataset.shape, num_steps, betas, one_minus_alphas_bar_sqrt)
fig, axs = plt.subplots(1, 10, figsize=(28, 3))
for i in range(1, 11):
cur_x = x_seq[i * 10].detach()
axs[i - 1].scatter(cur_x[:, 0], cur_x[:, 1], color='red', edgecolor='white');
axs[i - 1].set_axis_off();
axs[i - 1].set_title('$q(\mathbf{x}_{' + str(i * 10) + '})$')
plt.show()
#####################9、动画演示扩散过程和逆扩散过程##################################
'''import io
from PIL import Image
imgs = []
for i in range(100):
plt.clf()
q_i = q_x(dataset, torch.tensor([i]))
plt.scatter(q_i[:, 0], q_i[:, 1], color='red', edgecolor='white', s=5);
plt.axis('off');
img_buf = io.BytesIO()
plt.savefig(img_buf, format='png')
img = Image.open(img_buf)
imgs.append(img)
reverse = []
for i in range(100):
plt.clf()
cur_x = x_seq[i].detach()
plt.scatter(cur_x[:, 0], cur_x[:, 1], color='red', edgecolor='white', s=5);
plt.axis('off')
img_buf = io.BytesIO()
plt.savefig(img_buf, format='png')
img = Image.open(img_buf)
reverse.append(img)
imgs = imgs +reverse
imgs[0].save("diffusion.gif",format='GIF',append_images=imgs,save_all=True,duration=100,loop=0)''






 浙公网安备 33010602011771号
浙公网安备 33010602011771号