树状数组
树状数组总结
前言
树状数组是数据结构中的一股清流,代码简洁,思路清晰,又好理解 qwq。
前置芝士
lowbit:https://www.cnblogs.com/zhouruoheng/p/18003331
简介
树状数组是一种基于 lowbit 的用于维护 \(n\) 个数前缀和信息的数据结构。
支持:
- 快速求前缀和,复杂度为 \(O(\log{n})\)。
- 修改某一个数,复杂度为 \(O(\log{n})\)。
可以看下表:
| 数组 | 前缀和数组 | 树状数组 | 线段树 | |
|---|---|---|---|---|
| 单点修改 | \(O(1)\) | \(O(n)\) | \(O(\log{n})\) | \(O(\log{n})\) |
| 查询 | \(O(n)\) | \(O(1)\) | \(O(\log{n})\) | \(O(\log{n})\) |
树状数组将各操作优化成 \(O(\log{n})\),且比线段树好写得多,能处理许多线段树能写的问题。
具体实现
存储
树状数组具体实现和 st 表差不多,尤其是区间划分。
首先,一个数可以用二进制表示:
设 \(i_1>i_2> \cdots >i_k\),那么区间 \([1,n]\) 就可以被分成 \(\log{n}\) 即 \(k\) 个小区间:
长度分别为 \(2^{i_1}\),\(2^{i_1}\),\(\dots\) ,\(2^{i_k}\)。
它们有个共同特点:若区间右端点为 \(x\),则区间长度就是 \(lowbit(x)\)。
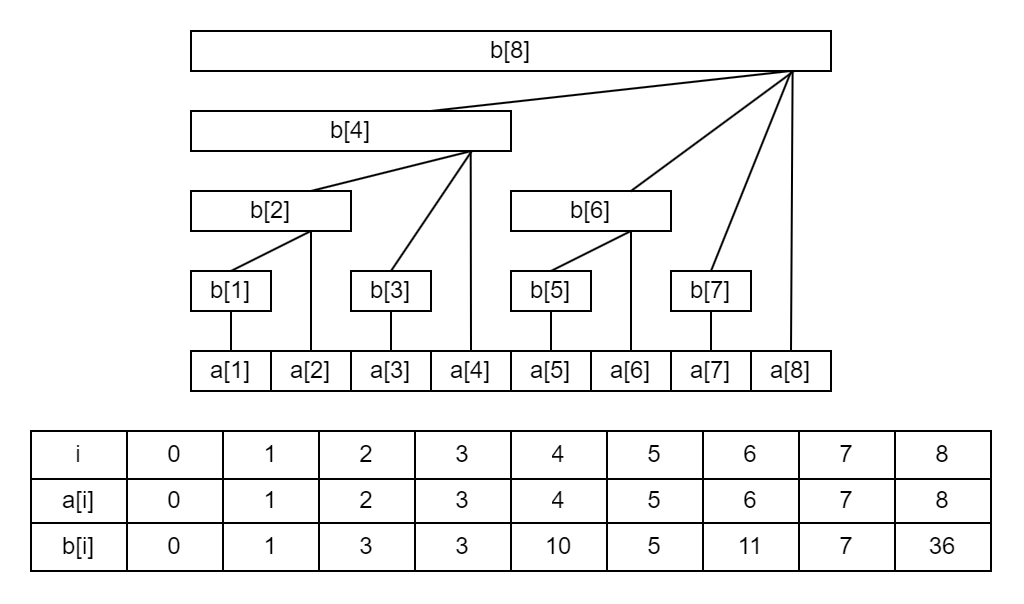
那么设存有 \(n\) 个数的数组 \(a\),用树状数组使用 \(c\) 来储存。
\(c_i\) 表示 \([i-lowbit(i)+1,i]\) 区间内的和,即将 \(i\) 作为右端点,长度为 \(lowbit(i)\) 的区间。数组 \(c\) 可以看作一个树形结构。
如下图:
查询
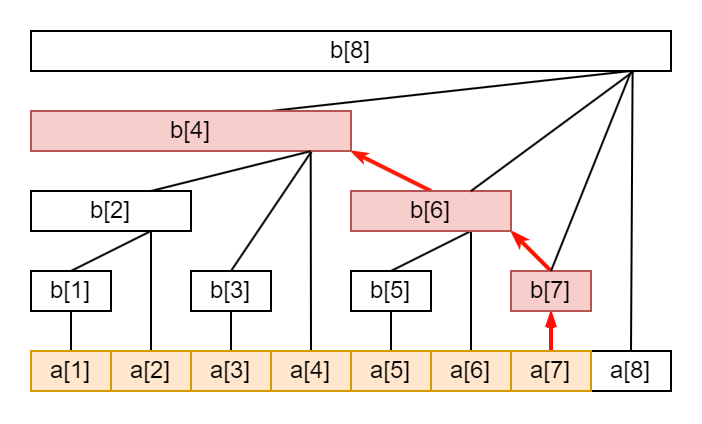
进行查询前缀和那么就要将原区间分解成若干小区间,就和分解正整数那样,然后相加。
在上面的处理出 \(c\) 数组的基础上,将 \(\log{n}\) 个区间和相加就能得到原数组的前缀和,例如求 \(a_1\) 到 \(a_i\) 的和 \(s_i\),直接将 \(c_i\) 加入答案,\(c_i\) 表示 \([i-lowbit(i)+1,i]\) 区间内的和,所以答案还需加上 \(a_1\) 到 \(a_{i-lowbit(i)}\) 的和,也就是 \(s_{i-lowbit(i)}\),再加上 \(c_{i-lowbit(i)}\) 一直操作,最后到 \(s_0\),就得到答案了。例如查询 \(s_7\),\(s_7=c_7+c_6+c_4\)。
code:
int sum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i)) ans+=c[i];
return ans;
}
修改
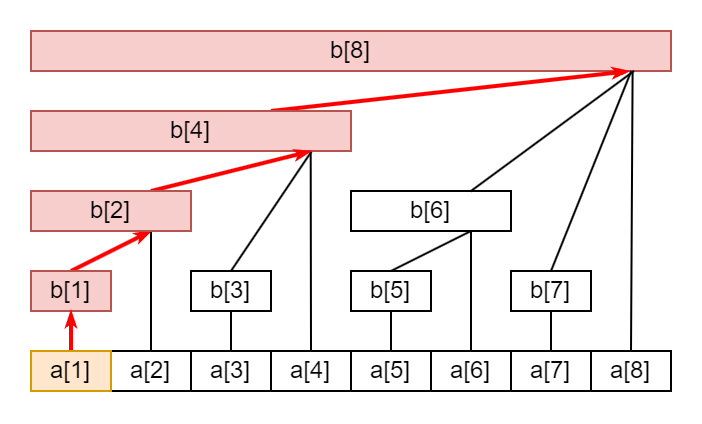
既然要进行单点修改,那么儿子一定会影响其父亲,因此我们必须修改所以有影响的点。由图可知,每个点都只有一个父亲,只需要一直往父亲那走就好了。那么父节点和子节点有什么关系呢?
显而易见,节点 \(x\) 的父节点是 \(x+lowbit(x)\),若是有闲功夫证明的话也可以证明下。
所以只要一直往父节点去,然后进行修改就可以了。
// 将a[x]加上y
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y;
}
初始化
有了修改操作后,那么就可以非常简单的进行初始化,将 \(a\) 数组中的值一次加入到树状数组中即可,复杂度为 \(O(n\log{n})\)。
void init()
{
for(int i=1;i<=n;i++) add(i,a[i]);
}
初始化还有一种更快的方法,时间复杂度为线性。先处理出前缀和,再直接给 \(c\) 数组赋值。不过一般情况下没有必要,用上面的就好。
int b[N];//a 的前缀和
void init()
{
for(int i=1;i<=n;i++)
{
b[i]=b[i-1]+a[i];
c[i]=b[i]-b[i-lowbit(i)];//[i-lowbit(i)-1,i]
}
}
例1 P3374 【模板】树状数组 1
https://www.luogu.com.cn/problem/P3374
分析
将上面所讲的内容结合一下即可。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int n,m,a[N],c[N];
int lowbit(int x)
{
return x&-x;
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y;
}
int sum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i)) ans+=c[i];
return ans;
}
int main ()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
add(i,a[i]);
}
while(m--)
{
int op,x,y;
cin>>op>>x>>y;
if(op==1) add(x,y);
else cout<<sum(y)-sum(x-1)<<"\n";
}
return 0;
}
例2 P3368 【模板】树状数组 2
https://www.luogu.com.cn/problem/P3368
分析
区间修改和单点查询,就像用普通数组一样思考,显然,差分数组就能轻易做到区间修改。用树状数组维护差分数组,就能轻易做到区间修改和单点查询。
- 区间修改:例如将 \([l,r]\) 的值加上 \(x\),只需要将 \(c_l\) 加上 \(x\),\(c_{r+1}\) 减去 \(x\)。
- 单点查询:查询 \(a_x\) 就是查 \([1,x]\) 的和,直接求就好了
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int n,m,a[N],c[N];
int lowbit(int x)
{
return x&-x;
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y;
}
int sum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i)) ans+=c[i];
return ans;
}
int main ()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],add(i,a[i]-a[i-1]);
while(m--)
{
int op,x,y,k;
cin>>op;
if(op==1)
{
cin>>x>>y>>k;
add(x,k);
add(y+1,-k);
}
else
{
cin>>x;
cout<<sum(x)<<"\n";
}
}
return 0;
}
例3
题目描述
既然已经知道了如何单点修改区间查询以及区间修改和单点查询,那么能不能做到区间修改区间查询呢?
分析
首先肯定是可以的,且复杂度能比数组更优,只需要稍微使用一点点技巧。还是维护差分数组,区间修改还是那样,主要思考区间查询。\(a\) 为原数组,\(b\) 为差分数组,则有:
注意看 \(\sum_{i = 1}^{x}\sum_{j = 1}^{i} b_j\),将其展开来:
放到图中来看:
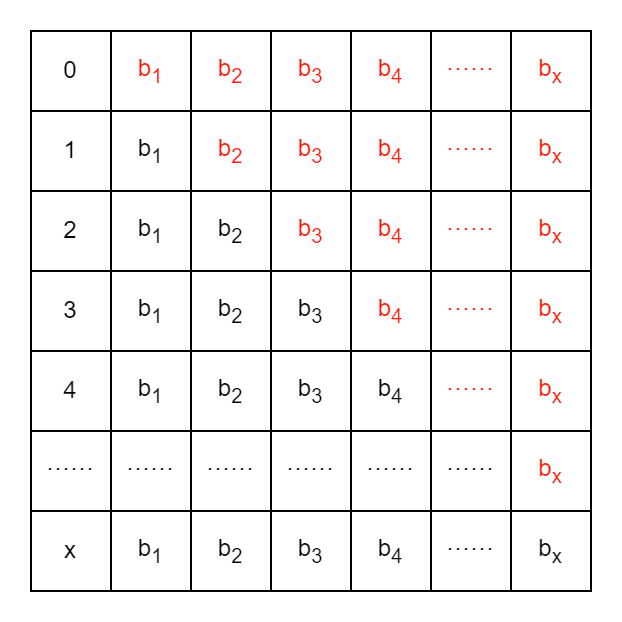
黑色数据相加就是所需,将其补全,整个表就是 \((x+1) \times (b_1+b_2+b_3+b_4+ \dots +b_x)\),可以看作前缀和。红色的竖着来看,就是 \(b_1+2 \times b_2+3 \times b_3+ \dots +x \times b_x\),其实也是个前缀和,\(i \times b_i\)。总的来说:
也就是说我们要维护两个前缀和,\(b_i\) 和 \(b_i \times i\)。
code
code 不保证都正确。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,m,a[N],c1[N],c2[N];
int lowbit(int x)
{
return x&-x;
}
void add(int c[],int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y;
}
int sum(int c[],int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i)) ans+=c[i];
return ans;
}
int query(int x)
{
return sum(c1,x)*(x+1)-sum(c2,x);
}
int main ()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
{
int b=a[i]-a[i-1];
add(c1,i,b);
add(c2,i,b*i);
}
while(m--)
{
int op,l,r,x;
cin>>op>>l>>r;
if(op==1)
{
cin>>x;
add(c1,l,x),add(c1,r+1,-x);
add(c2,l,l*x),add(c2,r+1,(r+1)*(-x));
}
else cout<<query(r)-query(l-1)<<"\n";
}
return 0;
}
例4 P1908 逆序对
https://www.luogu.com.cn/problem/P1908
分析
首先数据跨度大,可以离散化,离散化后用树状数组维护权值数组。以离散化后的值为下标,存贮出现的数量。\(s_i\) 表示小于等于 \(i\) 的数的个数,离散化后的值为 \(k\),从 \(1\) 到 \(n\) 遍历 \(a\) 数组,将 \(ans\) 加上 \(s_{k-1}\), \(a_k\) 加上 \(1\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+5;
int n,m,a[N],b[N],c[N];
int lowbit(int x)
{
return x&-x;
}
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i)) c[i]+=y;
}
int sum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i)) ans+=c[i];
return ans;
}
int main ()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
sort(b+1,b+n+1);
m=unique(b+1,b+n+1)-b-1;
ll ans=0;
for(int i=n;i;i--)
{
int k=lower_bound(b+1,b+m+1,a[i])-b;
ans+=sum(k-1);
add(k,1);
}
cout<<ans<<"\n";
return 0;
}
练习
tips
- 注意前缀和的范围,要不要开
long long。 - 树状数组维护的是前缀和数组,差分数组还是权值数组。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号