[探究] 数组循环移动的一种方式

（笔者为普通高三学生，无竞赛经验，如果你有更好的方法，请忽略本文）

最近刷信息技术做到一道题，设今天是星期 $k\,(k = 1, \,2,\,3 ,\,4,\, 5,\, 6,\, 7)$。求昨天是星期几？明天是星期几？ 这两个问题看似简单，实则隐含着深意，隐含着一种解决此类问题的思想。

答案是 $(k + 5)\,mod\,7 + 1$。它是如何被推导出来的呢？也许需要严格的数学证明，但是，对于一个追求效率的人来说，那些证明实在是繁冗拖沓，下面我提供一种很快的解决办法：

我称之为“启发推导法”。大概记得这种方法老师之前上课讲过，不过他研究得肯定没我透彻。“启发”的意思是，从一个猜测的答案开始，根据逻辑推理，逐渐达到正确的解。

 

• PART1-求“明天是星期几”

按照习惯性思维，我们应该很快能写出 $(k + 1)\,mod\,7$ 。这个公式在 k 为 $1 \sim 5$ 和 $7$ 时符合得很好，但是对 $k  =  6$ 时就无能为力了，为什么呢？因为对 $7$ 取模的结果最大只能是 $6$ 。从逻辑上这个公式就被推翻了——但它已经很接近正确的解了，确切地来说已经满足了 $\frac{6}{7}$ 的情况。怎么让结果能覆盖到 $7$ 呢？只需要加上一个 $1$ 就行了，但是别忘了在括号内减去加上的 $1$。即：$k\,mod\,7 + 1$。

它的确是符合所有的情况的。

• PART2-求“昨天是星期几”

对于这类情况的处理稍显复杂，同样我们先写出 $(k - 1)\,mod\,7$ ，但它显然不行，范围里就没有 $7$ 。怎么做呢？还是括号外 $+ 1$ ，括号内 $- 1$ 吗？这样 $k$ 代进去就是负数了。

我们知道对一个数取模时，加上它本身对取模结果没有影响，不妨先 $+7$ 以防止负数的出现？即 $(k + 6)\,mod\,7$，再按照原来的方法处理，就成了 $(k + 5)\,mod\,7 + 1$，符合所有情况。

---

上面只是一个引子，现在我们回归正题——实现数组的循环移动。

无疑，这个操作需要额外的存储空间，因为一个元素的移动必然引起一系列元素的连锁移动，不能直接覆盖否则数据会丢失。考虑一个数组 $a$ ，它存放着待循环移动的数据，现在我们开一个数组 $b$ 来存放循环移动后的数据，此时就需要用到引子里面的思想方法，不多说，直接呈上代码：

#include <vector>
#include <iostream>

void printArray(const std::vector<int> &v)
{
    for (const auto& object : v)
        std::cout << object << " ";
    std::cout << std::endl;
}

int main()
{
    std::vector<int> a{ 1,2,3,4,5,6,7,8 };
    int n = a.size(); // a数组的元素个数
    int m = 1; // 循环向右移动m个元素
    std::vector<int> b(n, 0);

    std::cout << "Array A: ";
    printArray(a);
    std::cout << std::endl;

    for (; m < n; m++)
    {
        for (int i = 0; i < a.size(); i++)
            b[(i + m - 1) % n + 1] = a[i];
        std::cout << "Array B: ";
        printArray(b);
    }
    return 0;
}

 

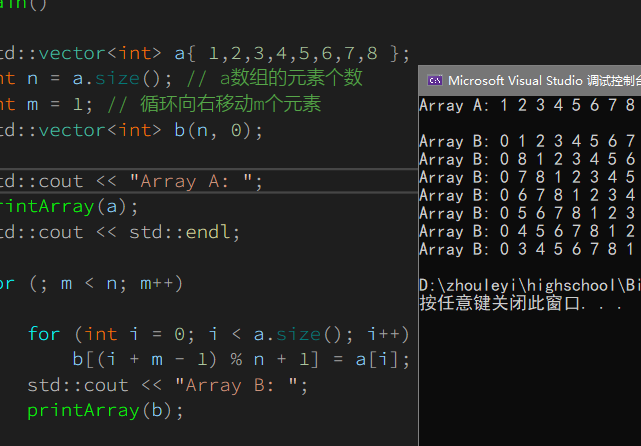
 运行代码，却发现结果和预期不符，为什么呢？因为我们前面的公式是针对 $1\sim n$ 的。

但是，不说以不变应万变，但只要稍作改动—— $0\sim n-1$ 不就是 $1\sim n$ 吗? 我们可以先 $+1$ ，将其代入公式，再 $-1$ 恢复原状：

for (; m < n; m++)
    {
        for (int i = 0; i < a.size(); i++)
            b[(i + m) % n] = a[i];
        std::cout << "Array B: ";
        printArray(b);
    }

 

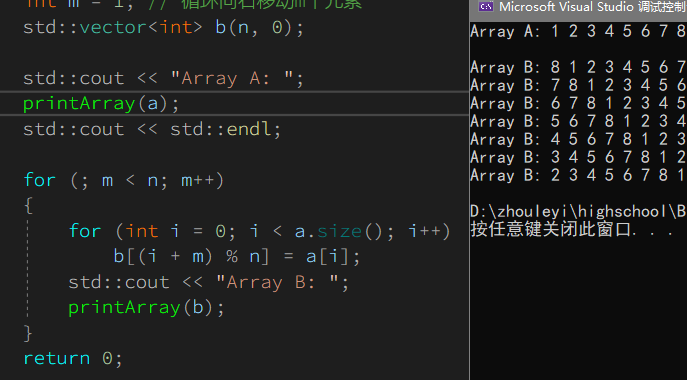
同样地，左移的代码也就顺理成章：

for (; m < n; m++)
    {
        for (int i = 0; i < a.size(); i++)
            b[(i - m % n + n) % n] = a[i]; // m % n 防止索引为负数
        std::cout << "Array B: ";
        printArray(b);
    }

 

现在我们来考虑一个变形，之前一直都是对 $a[i]$ 赋值，能不能对 $b[i]$ 赋值呢？其实原理完全一样，此处不再赘述。

--END--  距离第一次选考还有 $40$ 天。

---

UPD（2023-04-28）：更新了 $\LaTeX$ 。（感觉我上大学的这两年（自）学的东西比过去十几年的都多...）