二叉树的深度
题目描述
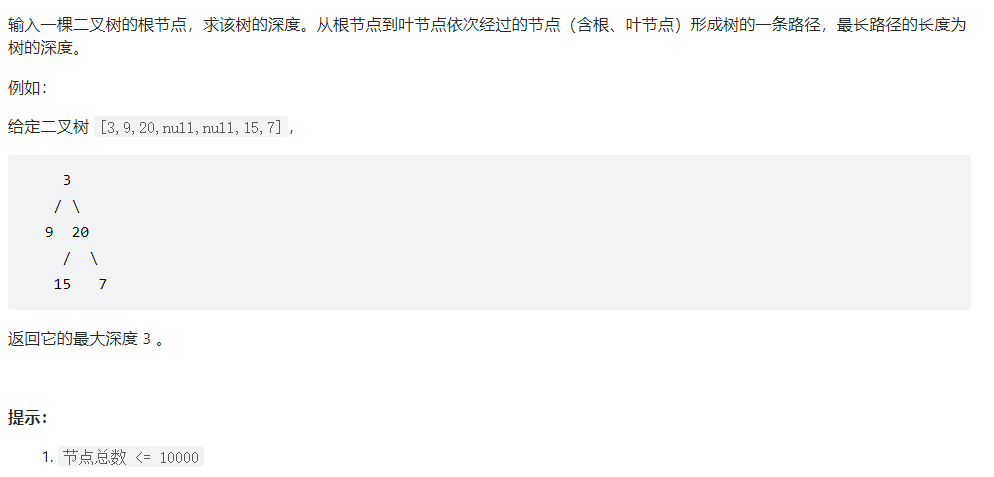
思路
动态规划+回溯
求深度,就是求左右子树深度的最大值再+1
层序遍历
通过层序遍历,根据出队或者入队的次数判定
代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
int leftD=maxDepth(root.left)+1;
int rightD=maxDepth(root.right)+1;
return leftD>rightD?leftD:rightD;
}
}
复杂度分析
时间复杂度
O(N),会遍历到每个节点
空间复杂度
O(N),退回为链表的时候
反思不足
思路
平衡二叉树
题目描述
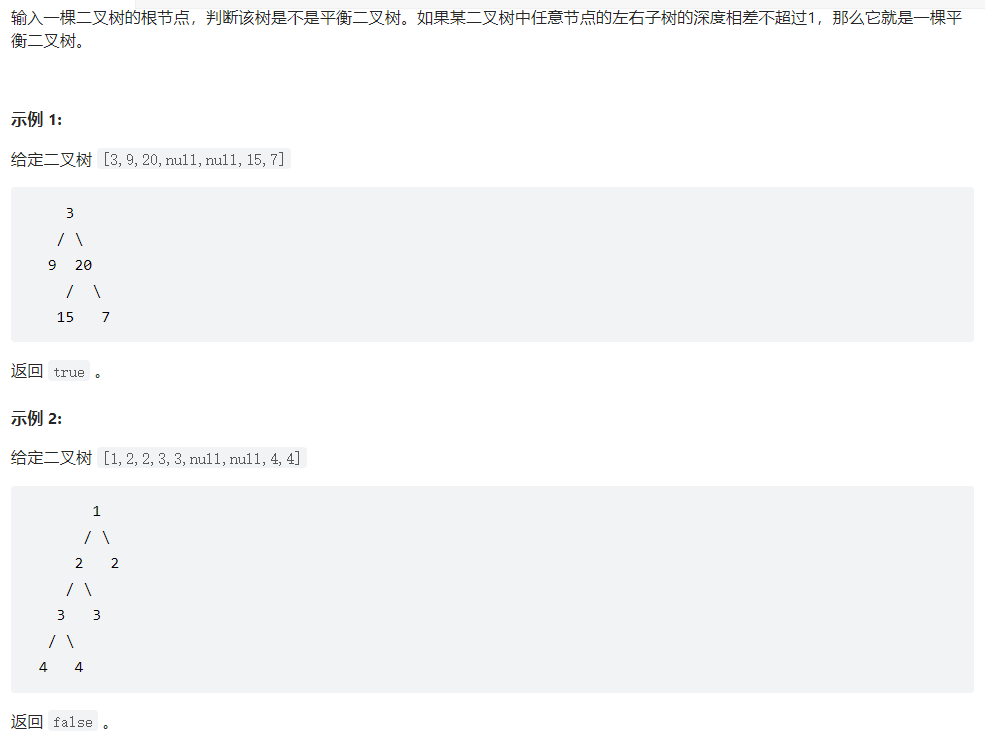

思路
二叉树的深度+剪枝
对每个节点的左右子节点都进行一次判定,判断其深度之差的绝对值是否大于1
可以优化,通过剪枝,如果已经确定了不是平衡树了,就没有必要再进行多余的递归调用,直接往上返回即可
代码实现
class Solution {
boolean result=true;
public boolean isBalanced(TreeNode root) {
nodeDepth(root);
return result;
}
public int nodeDepth(TreeNode node){
if(node==null||result==false){
return 0;
}
int leftD=nodeDepth(node.left)+1;
int rightD=nodeDepth(node.right)+1;
if(Math.abs(leftD-rightD)>1){
result=false;
}
return Math.max(leftD,rightD);
}
}
复杂度分析
时间复杂度
O(N)
空间复杂度
O(N)
反思不足
思路
剪枝避免无意义的函数调用
一旦结果确定就要避免无意义的成本支出



