代码随想录day 53 || 图论4

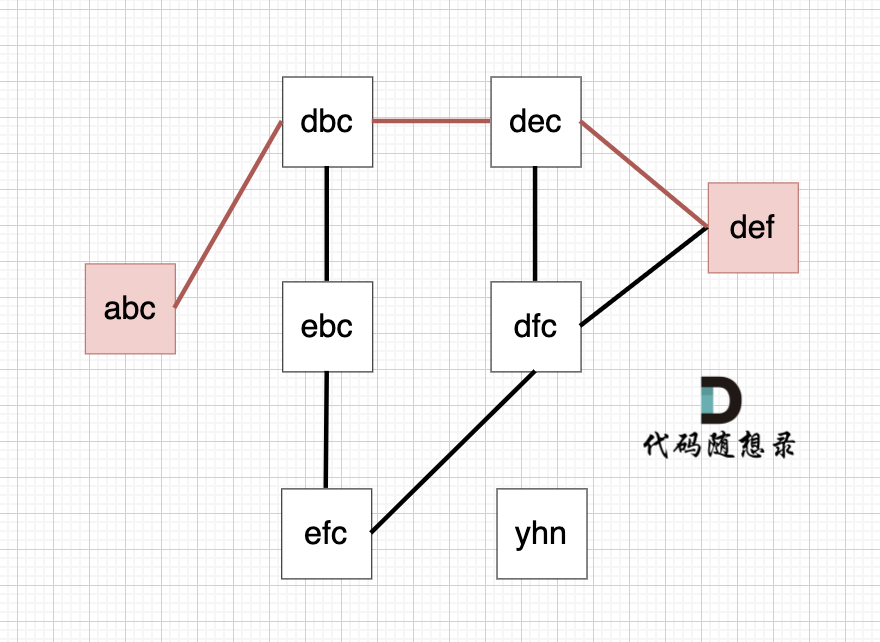
字符串接龙

copy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

var queue *list.List
var visitMap map[string]bool

func main() {
	var count int
	fmt.Scanf("%d", &count)
	var startStr, endStr string
	fmt.Scanf("%s %s", &startStr, &endStr)

	var strList = make([]string, count)
	for i := 0; i < count; i++ {
		var str string
		fmt.Scanf("%s", &str)
		strList[i] = str
	}
	fmt.Println(startStr, endStr, strList)

	queue = list.New()
	queue.PushBack(startStr)
	visitMap = make(map[string]bool, len(strList)) // 存放字符的使用状态
	for _, v := range strList {
		visitMap[v] = false
	}

	bfs(endStr, strList)
}

func bfs(target string, strList []string) {
	// 本题的思路是构建无向图，然后广搜得到最短路径
	// 但是具体怎么实现？先构建再广搜？并不是，是一边广搜一边半构建
	// 具体过程是，从startStr出发，对于每一个字符，尝试使用26个字母替换，如果替换后的新字串出现在strlist中，那么加入队列，路径+1，直到最终找到endStr
	
	// todo: 广搜如何记录层数，也就是路径深度，应该是每一层都标记一下入队长度，如果该层完全出队，层度+1，太长就不写了

	for queue.Len() > 0 {
		node := queue.Remove(queue.Front()).(string)
		nodeRune := []rune(node)
		for idx, _ := range nodeRune {
			for i := 0; i < 26; i++ {
				newStr := nodeRune
				newStr[idx] = rune(i + 'a')

				// 如果直接变成target，返回
				if string(newStr) == target {
					count++
					return
				}

				// 遇到字典元素， 并且没有使用过
				if v, ok := visitMap[string(newStr)]; ok && !v {
					visitMap[string(newStr)] = true
					queue.PushBack(string(newStr))
				}
			}

		}
	}

}

有向图完全可达性

copy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
package main

import (
	"container/list"
	"fmt"
)

var queue *list.List
var visited []bool

func main() {
	//var c, l int
	//fmt.Scanf("%d %d", &c, &l)
	//
	//// 构建邻接矩阵存储图
	//var graph = make([][]int, c)
	//for i, _ := range graph {
	//	graph[i] = make([]int, c)
	//}
	//for i := 0; i < l; i++ {
	//	var x, y int
	//	fmt.Scanf("%d %d", &x, &y)
	//	graph[x-1][y-1] = 1
	//}
	//for _, v := range graph {
	//	fmt.Println(v)
	//}

	c := 4
	//l := 4
	graph := [][]int{{0, 1, 1, 0}, {1, 0, 0, 1}, {0, 0, 0, 0}, {0, 0, 0, 0}}

	// dfs
	// 本题原理就是找到首个节点到所有节点是否路径可达，所以dfs判断两个节点是否存在路径（路径可达）
	for i := 1; i < c; i++ {
		visited = make([]bool, c)
		if dfs(0, i, graph) == false { // 任意一个节点不可达，就是false
			fmt.Printf("dfs %d false\n", i)
			break
		}
	}

	// bfs
	for i := 1; i < c; i++ {
		visited = make([]bool, c)
		visited[0] = true
		queue = list.New()
		queue.PushBack(0)
		if bfs(graph, i) == false {
			fmt.Printf("bfs %d false\n", i)
			break
		}
	}
	fmt.Println("true")
}

func dfs(start, stop int, graph [][]int) bool {
	// 递归终止条件，空，或者找到了target
	visited[start] = true // 标记节点已经遍历过
	if start == stop {
		return true
	}

	for idx, v := range graph[start] {
		if v == 1 && !visited[idx] {
			res := dfs(idx, stop, graph)
			if res { // 某次递归出现了目标，直接返回true
				return true
			}
		}
	}

	// 回溯
	visited[start] = false
	return false
}

func bfs(graph [][]int, target int) bool {
	for queue.Len() > 0 {
		node := queue.Remove(queue.Front()).(int)
		if node == target {
			return true
		}
		for i, v := range graph[node] {
			if v == 1 && !visited[i] {
				visited[i] = true
				queue.PushBack(i)
			}
		}
	}

	return false
}

463 岛屿周长

copy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
var dirPath = [4][2]int{{0,1}, {0,-1}, {1,0}, {-1,0}}
var sum int // 周长
var visited [][]bool
func islandPerimeter(grid [][]int) int {
	// 很简单的思路，计算所有的陆地，然后区分不同的周长
	// 三面环水，周长为3，两面，周长是2... 四周几格水周长就是几，边界也算作水
	sum = 0
	visited = make([][]bool, len(grid))
	for i, _ := range visited {
		visited[i] = make([]bool, len(grid[0]))
	}

	for i:=0; i<len(grid); i++ {
		for j:=0; j<len(grid[0]); j++ {
			if grid[i][j] == 1 && !visited[i][j] {
				dfs(i, j, grid)
			}
		}
	}
	return sum
}

func dfs(x, y int, graph [][]int) {

	if graph[x][y] == 0 || visited[x][y] {
		visited[x][y] = true
		return
	}
	visited[x][y] = true

	for _, dir := range dirPath {
		next_x, next_y := x + dir[0], y+ dir[1]
		if next_x < 0 || next_y<0 || next_x >= len(graph) || next_y >= len(graph[0]) {
			sum += 1  // 当前陆地的周边是边界，视为水，周长+1
			continue
		}
		if graph[next_x][next_y] == 0 { // 当前陆地的周边是水，周长+1
			sum += 1
		}
		if graph[next_x][next_y] == 1 && !visited[next_x][next_y] {
			// 是新大陆
			dfs(next_x, next_y, graph)
		}
	}
}

本文作者：周公瑾55

本文链接：https://www.cnblogs.com/zhougongjin55/p/18401501

版权声明：本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。

版权声明：本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。