图论
基础定义
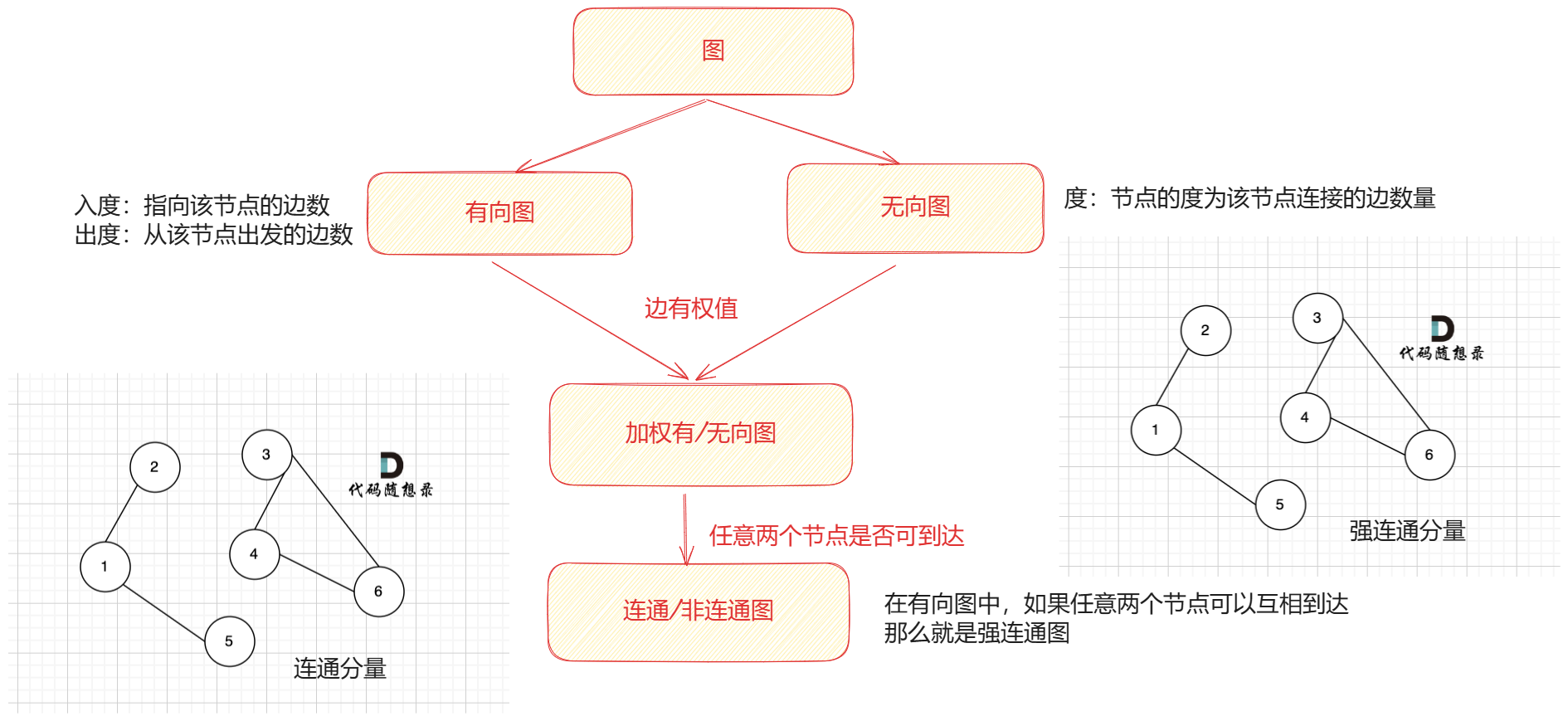
图的构造方式
1,邻接矩阵
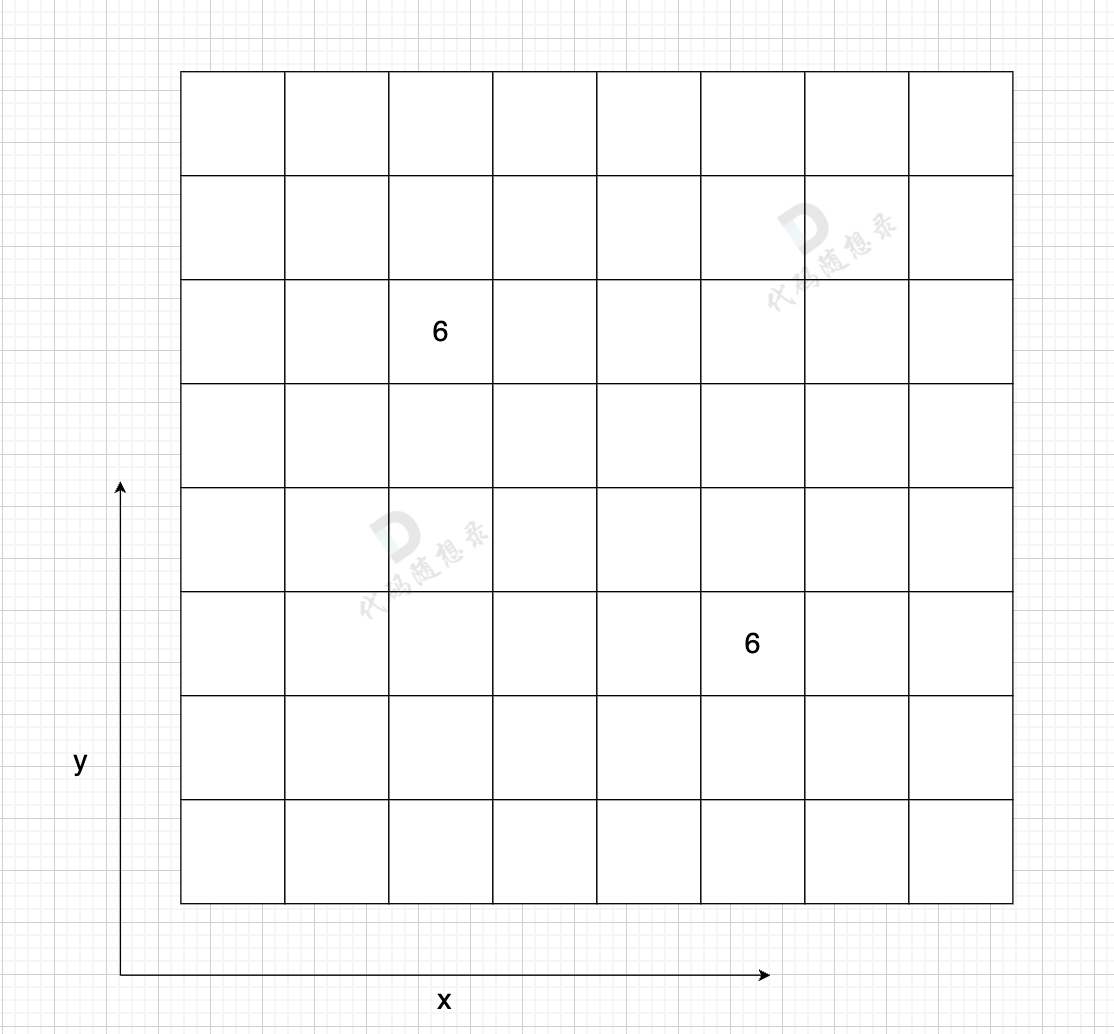
矩阵位置array[i][j] = k, i表示节点i,j表示节点j,[i][j] 表示i-->j存在一条边,k表示的是边的权重
邻接矩阵的优点:
表达方式简单,易于理解
检查任意两个顶点间是否存在边的操作非常快
适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
缺点:
遇到稀疏图,会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵,造成时间浪费
- 遍历
邻接矩阵的遍历方式大致是按照节点所在的行进行遍历,dfs是找到首个非空邻接点递归,bfs是找到行所有非空临界点入队
package main
import "fmt"
// 邻接矩阵表示图
var graph = [][]int{
{0, 1, 0, 0},
{0, 0, 1, 1},
{1, 0, 0, 1},
{0, 0, 0, 0},
}
// 访问标记数组
var visited = make([]bool, len(graph))
// 路径存储
var path []int
// DFS 函数
func DFS(vertex int, target int) bool {
visited[vertex] = true
path = append(path, vertex)
if vertex == target {
return true
}
for i, connected := range graph[vertex] {
if connected == 1 && !visited[i] {
if DFS(i, target) {
return true
}
}
}
path = path[:len(path)-1] // 回溯
visited[vertex] = false // 回溯
return false
}
func main() {
start := 0
target := 3
if DFS(start, target) {
fmt.Println("存在路径从顶点", start, "到顶点", target, ":", path)
} else {
fmt.Println("不存在路径从顶点", start, "到顶点", target)
}
}
package main
import "fmt"
// 邻接矩阵表示图
var graph = [][]int{
{0, 1, 0, 0},
{0, 0, 1, 1},
{1, 0, 0, 1},
{0, 0, 0, 0},
}
// 访问标记数组
var visited = make([]bool, len(graph))
// 路径存储
var path []int
// 队列实现
type Queue []int
func (q Queue) Push(x int) {
q = append(q, x)
}
func (q Queue) Pop() (int, bool) {
if len(q) == 0 {
return -1, false
}
front := q[0]
q = q[1:]
return front, true
}
func (q Queue) IsEmpty() bool {
return len(q) == 0
}
// BFS 函数
func BFS(start int, target int) bool {
queue := Queue{start}
visited[start] = true
path = append(path, start)
for !queue.IsEmpty() {
vertex, _ := queue.Pop()
if vertex == target {
return true
}
for i, connected := range graph[vertex] {
if connected == 1 && !visited[i] {
visited[i] = true
queue.Push(i)
path = append(path, i)
}
}
}
return false
}
func main() {
start := 0
target := 3
if BFS(start, target) {
fmt.Println("存在路径从顶点", start, "到顶点", target, ":", path)
} else {
fmt.Println("不存在路径从顶点", start, "到顶点", target)
}
}
2,邻接表
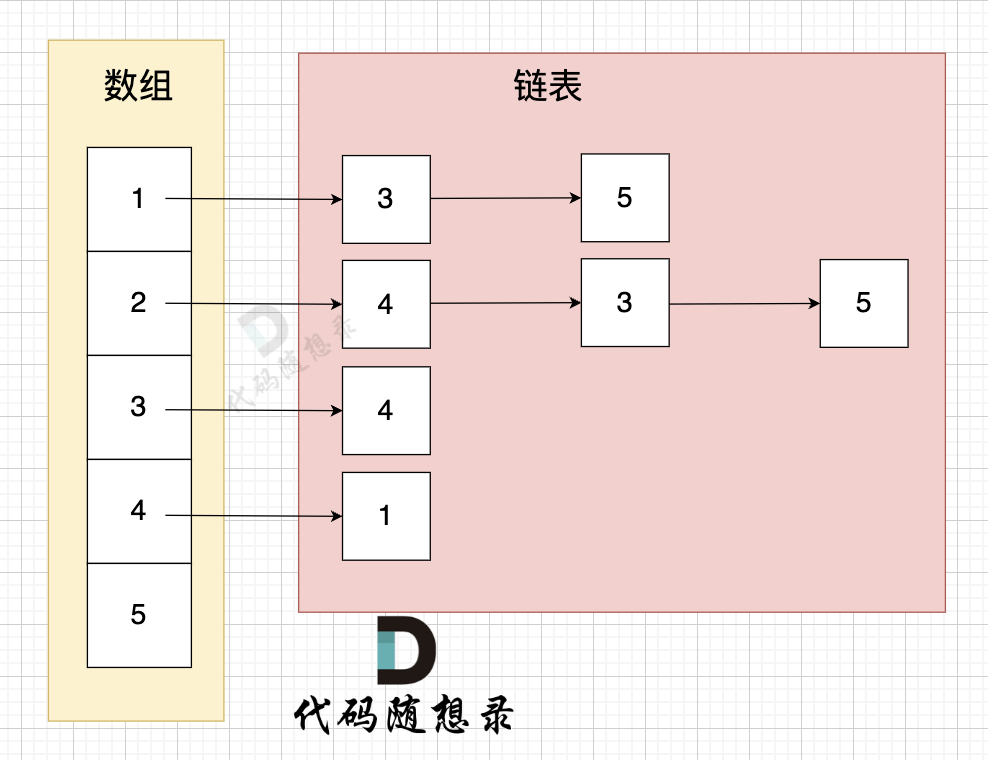
邻接表的数组存放的所有节点,每个位置对应的链表保存了该节点的所有度,eg: 1-->3-->5 代表节点1分别指向了节点3 和 节点5
邻接表的优点:
对于稀疏图的存储,只需要存储边,空间利用率高
遍历节点连接情况相对容易
缺点:
检查任意两个节点间是否存在边,效率相对低,需要 O(V)时间,V表示某节点连接其他节点的数量。
实现相对复杂,不易理解
- 遍历
邻接表遍历方式,相较于临界矩阵区别在于将行数据转换为链表,所以同样从起点出发,dfs找到起点.next() 递归,bfs是起点开始的整个链表除起点外全部入队
package main
import "fmt"
// 定义图的节点
type Graph struct {
adjList map[int][]int
visited map[int]bool
}
// 创建图
func NewGraph() *Graph {
return &Graph{
adjList: make(map[int][]int), // 这里使用数组实现链表
visited: make(map[int]bool), // 维护数组使用状态
}
}
// 添加边
func (g *Graph) AddEdge(v, w int) {
g.adjList[v] = append(g.adjList[v], w)
// 无向图还需要添加这行
// g.adjList[w] = append(g.adjList[w], v)
}
// DFS 实现
func (g *Graph) DFS(v int) {
g.visited[v] = true
fmt.Printf("访问顶点 %d\n", v)
for _, neighbor := range g.adjList[v] {
if !g.visited[neighbor] {
g.DFS(neighbor)
}
}
}
// BFS 实现
func (g *Graph) BFS(start int) {
queue := make([]int, 0)
queue = append(queue, start)
g.visited[start] = true
for len(queue) != 0 {
v := queue[0]
queue = queue[1:]
fmt.Printf("访问顶点 %d\n", v)
for _, neighbor := range g.adjList[v] {
if !g.visited[neighbor] {
g.visited[neighbor] = true
queue = append(queue, neighbor)
}
}
}
}
func main() {
g := NewGraph()
// 添加边,构建图
g.AddEdge(0, 1)
g.AddEdge(0, 2)
g.AddEdge(1, 2)
g.AddEdge(2, 0)
g.AddEdge(2, 3)
g.AddEdge(3, 3)
fmt.Println("DFS:")
g.DFS(0)
fmt.Println("\nBFS:")
g.BFS(0)
}
797 图所有路径
var path []int
var res [][]int
func allPathsSourceTarget(graph [][]int) [][]int {
// 本体是一个有向图,参数已经给出了邻接表的结构
// 本题是搜索路径,先考虑dfs,深度优先,原理是先一条路走到头,然后回溯,走下一条路
path = []int{0}
res = [][]int{}
dfs(graph, graph[0], len(graph)-1)
return res
}
func dfs(graph [][]int, route []int, target int) { // 回溯参数返回值
// 回溯终止条件 + 收集结果
if path[len(path) - 1] == target{
var copypath = make([]int, len(path))
copy(copypath, path)
res = append(res, copypath)
return
}
if len(route) == 0{
return
}
// for{单次回溯逻辑}
for i:=0; i<len(route); i++ {
path = append(path, route[i])
dfs(graph, graph[route[i]], target)
path = path[ : len(path) - 1]
}
return
}






 浙公网安备 33010602011771号
浙公网安备 33010602011771号