代码随想录day49 || 42、接雨水 84、柱状图中最大的矩形

42、接雨水

func trap(height []int) int {
	// 双指针思路，按照列计算雨水高度，分别计算每一列左右高于当前高度的最高柱子高度，然后通过min(left, right) - height[i] 得出当前列的雨水体积
	var res int
	var left, right int
	for i:=1; i<len(height)-1; i++ {
		left, right = height[i], height[i]
		for j:=i+1; j<len(height); j++ {
			if height[j] > right {
				right = height[j]
			}
		}
		for j:=i-1; j>=0; j-- {
			if height[j] > left {
				left = height[j]
			}
		}


		res += (min(left, right) - height[i]) * 1
	}

	return res
}
// 时间复杂度是n^2, 空间是1

// 上面解法对于左右最高高度计算涉及到重复，所以考虑空间换时间，用两个数组分别记录当前位置的左右最高高度
func trap(height []int) int {
	// 双指针思路，按照列计算雨水高度，分别计算每一列左右高于当前高度的最高柱子高度，然后通过min(left, right) - height[i] 得出当前列的雨水体积
	var res int
	var left = make([]int, len(height))
	var right = make([]int, len(height))

	left[0] = height[0]
	for i:=1; i<len(height)-1; i++ {
		left[i] = max(height[i], left[i-1])
	}
	right[len(height) - 1] = height[len(height) - 1]
	for i:=len(height)-2; i>=0; i--{
		right[i] = max(height[i], right[i+1])
	}

	//fmt.Println(left, right)
	for i:=1; i<len(height)-1; i++ {
		res += (min(left[i], right[i]) - height[i]) * 1
	}

	return res
}

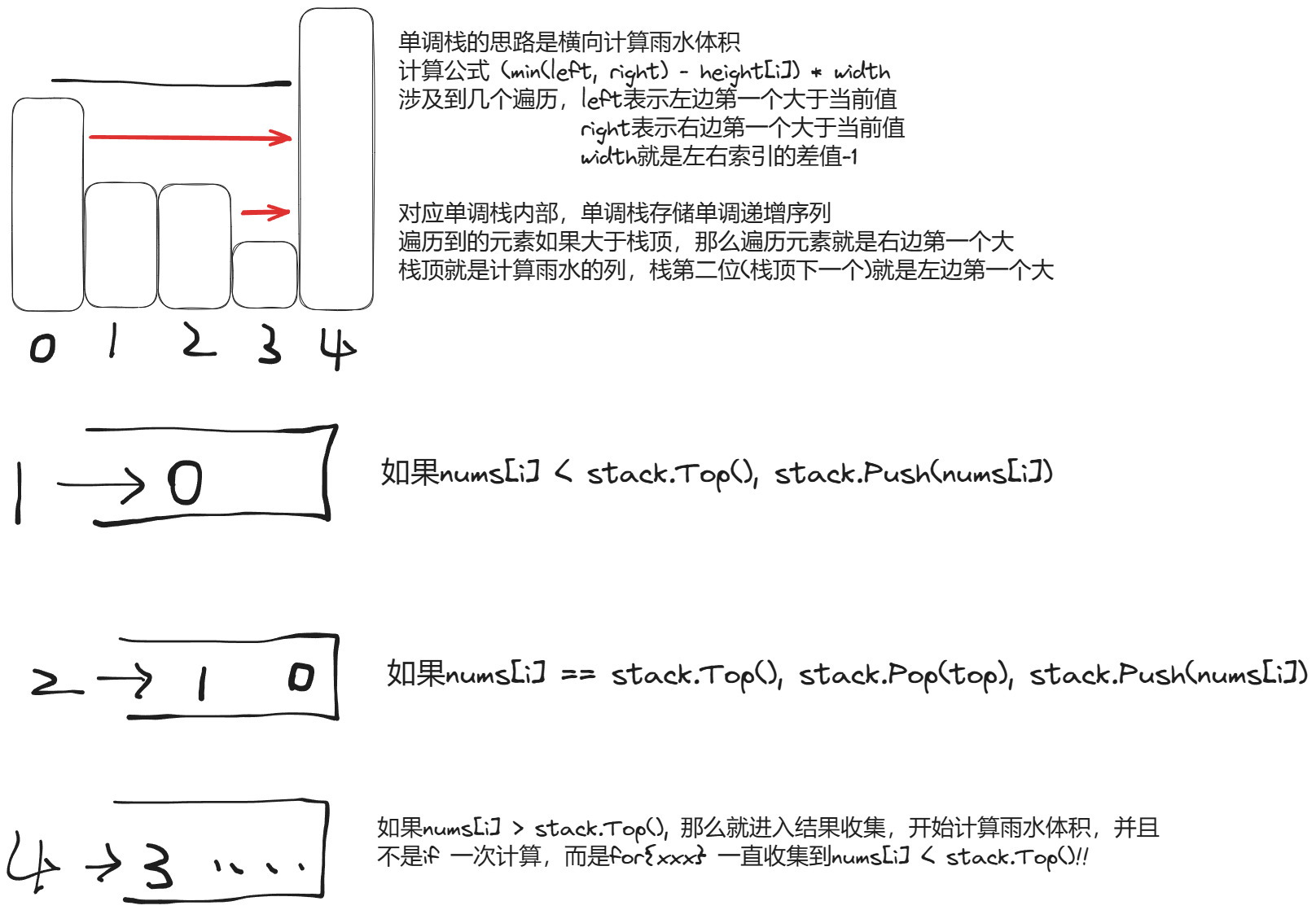
// 单调栈解法, 坑太多，注意单调栈保存的是索引！！！！！，别直接比较了，要取heithg[idx]
func trap(height []int) int {
	// 单调栈，
	var res int
	var stack []int
	for i:=0; i<len(height); i++{
		for len(stack) > 0 && height[i] >= height[stack[len(stack) - 1]] {
			top := stack[len(stack) - 1]
			stack = stack[ : len(stack) - 1]
			if len(stack) > 0 {
				left := stack[len(stack) - 1]
				right := i
				res += (min(height[left], height[right]) - height[top]) * (right - left - 1)
			}
		}
		stack = append(stack, i)
	}
	return res
}

84、柱状图中最大的矩形

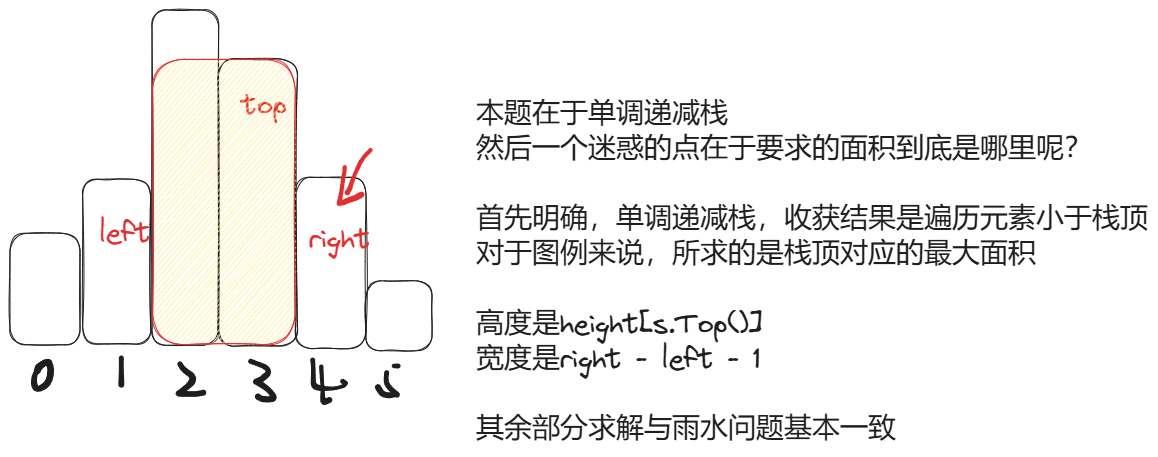
func largestRectangleArea(heights []int) int {
	// 单调栈 找到左右第一个小于当前元素的位置，然后计算面积
	// 递减栈
	// 大于栈顶 入栈  小于等于 计算面积
	if len(heights) == 1{
		return heights[0]
	}
	var m int
	// 细节首尾+0 // 分别处理[2,3,4]  [4,3,2] 这两种单调的样例
	heights = append([]int{0}, heights...)
	heights = append(heights, 0)
	var stack []int
	stack = append(stack, 0)
	for i:=0; i<len(heights); i++ {
		for len(stack) > 0 && heights[i] <= heights[stack[len(stack) - 1]] {
			top := stack[len(stack) - 1]
			stack = stack[: len(stack) - 1]
			if len(stack) > 0 {
				var left, right, res int
				left = stack[len(stack) - 1]
				right = i
				res = heights[top] * (right - left - 1)
				m = max(m, res)
			}
		}

		stack = append(stack, i)
	}
	return m
}