代码随想录day45 || 115 不同子序列, 583 两个字符串删除操作, 72 编辑距离

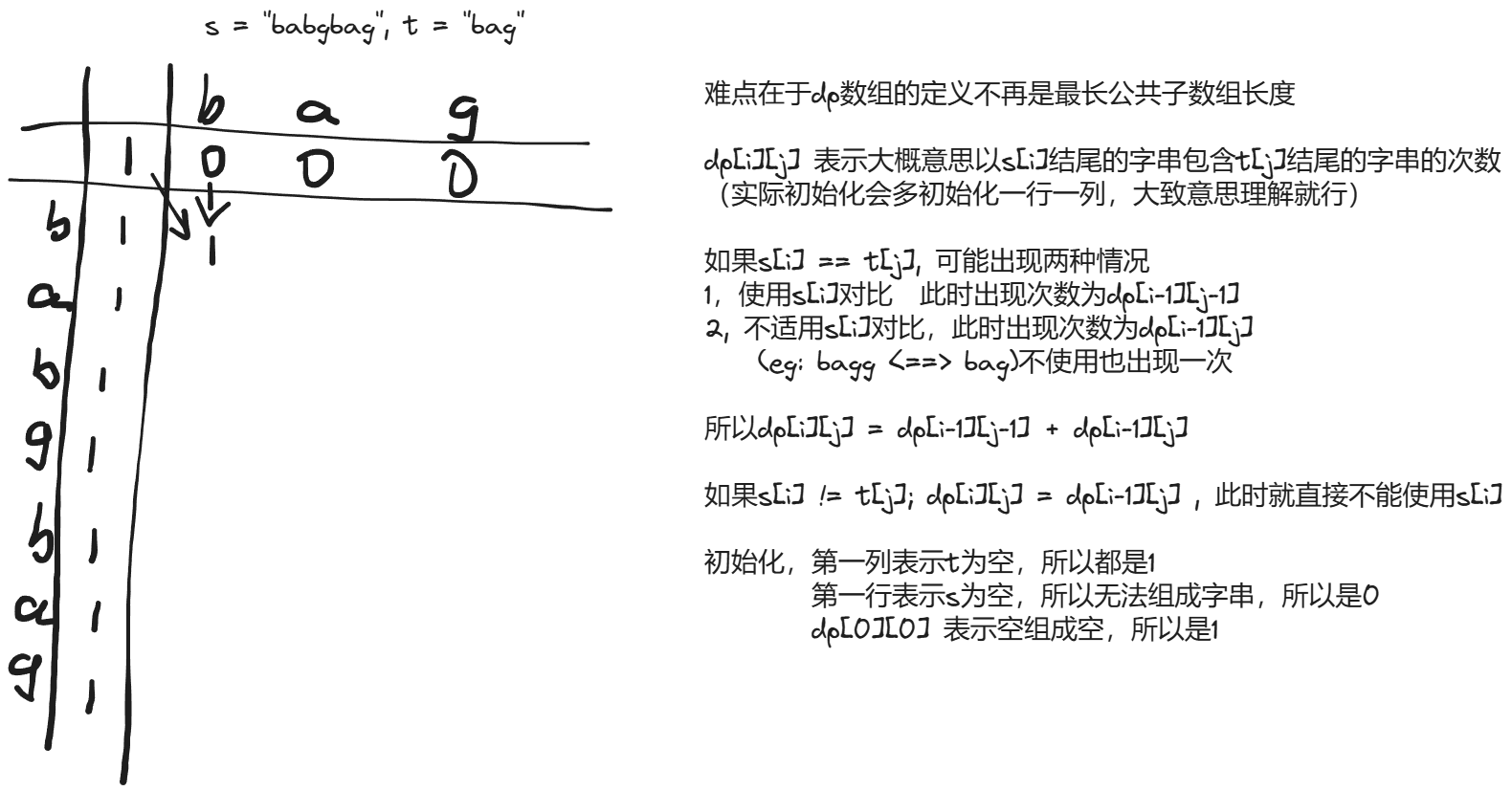
115 不同子序列

func numDistinct(s string, t string) int {
	// 动态规划，思考一下判断连续和不连续的区别，如果相等都是左上角+1， 如果不等，连续情况就是直接等于左上角，不连续情况直接归零
	// dp[i][j] 表示s[i] 中存在 t[j] 结尾的的个数
	// 递推公式，不要求连续字串，所以，如果s[i] != t[j] {dp[i][j] = dp[i-1][j]} else {dp[i][j] = dp[i-1][j-1]+dp[i-1][j]}
	// 多初始化一行一列 dp[0][0] = 1  dp[0][j] = 0  dp[i][0] = 1
	// print

	if len(t) > len(s) {
		return 0
	}

	var dp = make([][]int, len(s) + 1)
	for idx, _ := range dp {
		dp[idx] = make([]int, len(t) + 1)
		dp[idx][0] = 1
	}

	for i:=0; i<len(s); i++ {
		for j:=0; j<len(t); j++{
			if s[i] == t[j] {
				dp[i+1][j+1] = dp[i][j] + dp[i][j+1]
			}else {
				dp[i+1][j+1] = dp[i][j+1]
			}
		}
	}
	//fmt.Println(dp)
	return dp[len(s)][len(t)]
}

583 两个字符串删除操作

func minDistance(word1 string, word2 string) int {
	// 两种解题思路，第一种取巧，求两个字串的最长公共子序列，然后两个长度相加-公共*2 = 操作步数
	// 正常思路比较难
	// dp[i][j] 表示word1[i]结尾到word2[j]结尾相同需要删除的次数
	// if word1[i] == word2[j] {dp[i][j] = dp[i-1][j-1]} else {dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1, dp[i-1][j-1]+2)}
	// dp[i][0] = i  dp[0][j] = j
	// 正序遍历word1，正序word2
	// print

	var dp = make([][]int, len(word1) + 1)
	for i, _ := range dp {
		dp[i] = make([]int, len(word2) + 1)
		dp[i][0] = i
		if i == 0 {
			for j, _ := range dp[0] {
				dp[0][j] = j
			}
		}
	}

	for i:=0; i<len(word1); i++ {
		for j:=0; j<len(word2); j++{
			if word1[i] == word2[j] { // 此时不需要删除
				dp[i+1][j+1] = dp[i][j]
			}else {
				// 1, 删除word1[i]
				up := dp[i][j+1] + 1
				// 2, 删除word2[j]
				left := dp[i+1][j] + 1
				// 3, 两个都删除, 其实这里情况要么等于第一种，要么等于第二种
				ul := dp[i][j] + 2
				fmt.Println(up, left, ul)
				dp[i+1][j+1] = min(up, min(left, ul))
			}
		}
	}
	//fmt.Println(dp)
	return dp[len(word1)][len(word2)]
}

72 编辑距离

func minDistance(word1 string, word2 string) int {
	// 思路，想比较于两个字串删除操作题目，此题操作更多，所以dp公式判断如果不等可能更加复杂
	// dp[i][j] 代表w1[i] 结尾 和w2[j] 结尾相同需要最小操作数量
	// if w1[i] == w2[j] {dp[i][j] = dp[i-1][j-1]} // 相等不需要操作
	// 不等， 1, 删除w1[i] dp[i-1][j]+1
	//       2, 删除w2[j] dp[i][j-1]+1
	//       3, 两个都删除 dp[i-1][j-1] + 2
	//       4, 替换任意一个,此时两个就相等了  dp[i-1][j-1] + 1
	//       5, w1插入一个w2[j], 此时就是同时删除两个w2[j], 所以是dp[i][j-1] + 1
	//       6, w2插入一个w1[i], 同理 dp[i-1][j] + 1
	// 总结 dp[i][j] = min(dp[i-1][j]+1, dp[i][j-1]+1, dp[i-1][j-1]+1)

	// dp[0][j] = j  dp[i][0] = i
	// 根据dp定义进行遍历
	// print
	var dp = make([][]int, len(word1) + 1)
	for i, _ := range dp {
		dp[i] = make([]int, len(word2) + 1)
		dp[i][0] = i
		if i == 0 {
			for j, _ := range dp[0] {
				dp[0][j] = j
			}
		}
	}

	for i:=0; i<len(word1); i++ {
		for j:=0; j<len(word2); j++{
			if word1[i] == word2[j] { // 此时不需要删除
				dp[i+1][j+1] = dp[i][j]
			}else {
				dp[i+1][j+1] = min(dp[i][j+1] + 1, min(dp[i+1][j] + 1, dp[i][j] + 1))
			}
		}
	}
	//fmt.Println(dp)
	return dp[len(word1)][len(word2)]
}