代码随想录day34 || 62 不同路径，63 不同路径||，343整数拆分，96 不同搜索二叉树

不同路径

copy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func uniquePaths(m int, n int) int {
	// dp五部曲
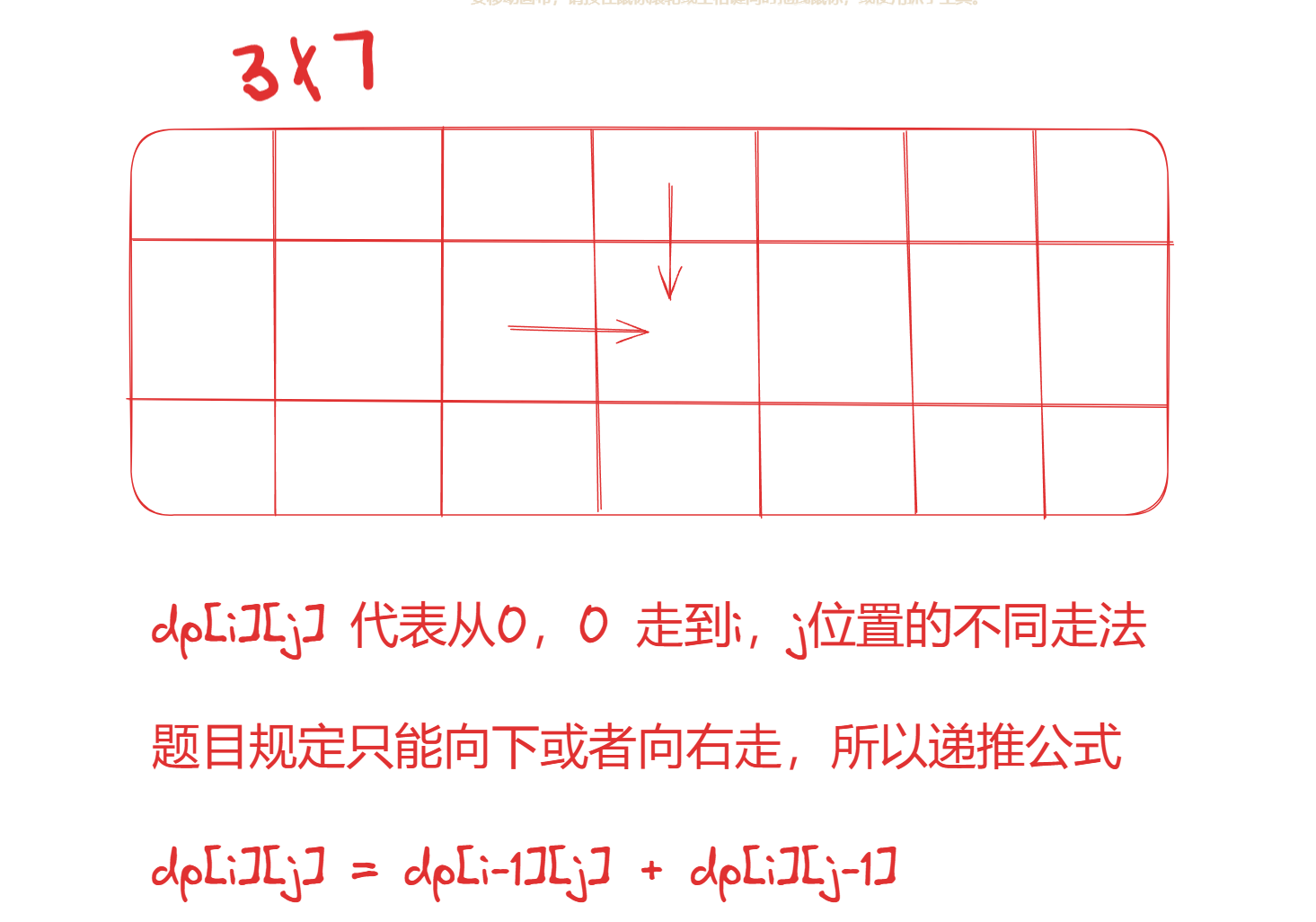
	// dp数组以及下标的含义  dp[i][j]代表从0，0 走到i，j的不同路径条数
	// 递推公式			dp[i][j] = dp[i-1][j] + dp[i][j-1]
	// dp数组的初始化     dp[i][0] == dp[0][j] = 1
	// 遍历顺序	外层按照行，内层按照列遍历
	// 打印dp
	var dp = make([][]int, m)
	for i:=0; i<m; i++{
		dp[i] = make([]int, n)
		for j:=0; j<n; j++{
			if i==0 || j==0 {
				dp[i][j] = 1
			}else {
				dp[i][j] = dp[i-1][j] + dp[i][j-1]
			}
		}
	}
	//fmt.Println(dp)
	return dp[m-1][n-1]
}

// 63 不同路径||

copy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func uniquePathsWithObstacles(obstacleGrid [][]int) int {
	// dp五部曲
	// 确定dp数组以及下标含义 dp[i][j] 表示1，1 到i, j不同路径数
	// 递推公式，if not 障碍 {dp[i][j] = dp[i-1][j] + dp[i][j-1]} else {dp[i][j] = 0}
	// 初始化dp dp[0][j] == dp[i][0] == 0, dp[1][1] = 1
	// 遍历顺序，先横向后纵向
	// 打印dp
	if obstacleGrid[0][0] == 1 {
		return 0
	}
	var dp = make([][]int, len(obstacleGrid)+1)
	for i, _ := range dp {
		dp[i] = make([]int, len(obstacleGrid[0])+1)
	}
	//dp[1][1] = 1 // 因为如果初始位置是障碍物，已经被最上面的return情况排除了
	//fmt.Println(dp)

	for i:=0; i<len(obstacleGrid); i++ {
		for j:=0; j<len(obstacleGrid[0]); j++{
			if obstacleGrid[i][j] == 1{
				// 障碍物
				dp[i+1][j+1] = 0
			} else if i==0 && j==0{
				dp[i+1][j+1] = 1
			} else {
				dp[i+1][j+1] = dp[i][j+1] + dp[i+1][j]
			}
		}
	}
	//fmt.Println(dp)
	return dp[len(obstacleGrid)][len(obstacleGrid[0])]
}

343 整数拆分

copy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func integerBreak(n int) int {
	// dp以及下标含义  dp[i] 代表拆分i能得到的最大积
	// 递推公式 dp[i] = max(j*(i-j), j*dp[i-j], dp[i]) //j*(i-j) 代表不拆分i-j得到积， j*dp[i-j]代表拆分i-j得到最大积
	// 初始化 dp[0] = 0 dp[1] = 0  dp[2] = (1x1) =1
	// 遍历顺序 3-->n
	// dayin
	var dp = []int{0,0,1}
	if n < 3 {
		return dp[n]
	}else {
		dp = append(dp, make([]int, (n+1)-3)...)
	}
	for i := 3; i <= n; i++{
		for j:=1; j<=i/2; j++{
			m := max(j*(i-j), j*dp[i-j])
			if m>dp[i] {
				dp[i] = m
			}
		}
	}
	//fmt.Println(dp)
	return dp[n]
}

96 不同搜索二叉树

copy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func numTrees(n int) int {
	// dp数组以及下标含义 dp[i] 表示 i个节点的二叉搜索树数量
	// 递推公式 dp[i] = Σ（0， i）(dp[j-1] * dp[i-j])  dp[j-1]代表左子树的数量 dp[i-j]代表右子树的数量，相乘就是j时的总组合，
	// 初始化 dp[0] = 1, dp[1] = 1, dp[2] = 2
	// 遍历顺序，i从0遍历到n， j每次从1遍历到i
	// 打印

	var dp = []int{1,1,2}
	if n <= 2 {
		return dp[n]
	}else {
		dp = append(dp, make([]int, n+1-3)...)
	}
	for i:=3; i<=n; i++{
		for j:=1; j<=i; j++{
			dp[i] += dp[j-1] * dp[i-j]
		}
	}
	fmt.Println(dp)
	return dp[n]
}

本文作者：周公瑾55

本文链接：https://www.cnblogs.com/zhougongjin55/p/18366935

版权声明：本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。