《算法》笔记 12 - 最短路径

• 加权有向图
• 数据结构
  • 加权有向边
  • 加权有向图
  • 最短路径
• 边的松弛
• Dijkstra算法

地图或者导航系统是最短路径的典型应用，其中顶点对应交叉路口，边对应公路，边的权重对应经过一段路的成本（时间或距离）。在这个模型中，问题可以被归纳为：找出从一个顶点到达另一个顶点的成本最小的路径。此外，网络路由、任务调度等也属于同类问题。

加权有向图

加权有向图是研究最短路径问题的模型。在加权有向图中，每条有向边都有一个与之关联的权重，路径的权重指路径上所有边的权重之和，所以在加权有向图中，求顶点v到w的最短路径问题就成了求顶点v到w的所有路径中权重最小者。

数据结构

加权有向边

加权有向边是构成加权有向图的基本单元，具有起点、终点和权重属性。

public class DirectedEdge {
    private final int v; 
    private final int w; 
    private final double weight; 

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public double weight() {
        return this.weight;
    }

    public int from() {
        return this.v;
    }

    public int to() {
        return this.w;
    }

    public String toString() {
        return String.format("%d->%d %.2f", v, w, weight);
    }
}

加权有向图

加权有向图的数据结构中，对加权有向边的组织方式与之前的有向图的组织方式类似，不同的是在邻接表中，之前存储的是图的顶点，现在则存储边。

public class EdgeWeightedDigraph {
    private static final String NEWLINE = System.getProperty("line.separator");
    private final int V; // vertex
    private int E; // edge
    private Bag<DirectedEdge>[] adj;

    public EdgeWeightedDigraph(int V) {
        this.V = V;
        this.E = 0;
        adj = (Bag<DirectedEdge>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<DirectedEdge>();
        }
    }

    public EdgeWeightedDigraph(In in) {
        this(in.readInt());
        int E = in.readInt();
        for (int i = 0; i < E; i++) {
            int v = in.readInt();
            int w = in.readInt();
            double weight = in.readDouble();
            DirectedEdge e = new DirectedEdge(v, w, weight);
            addEdge(e);
        }
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }

    public void addEdge(DirectedEdge e) {
        adj[e.from()].add(e);
        E++;
    }

    public Iterable<DirectedEdge> adj(int v) {
        return adj[v];
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " vertices, " + E + " edges " + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (DirectedEdge w : adj[v]) {
                s.append(w + " | ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }

    public Bag<DirectedEdge> edges() {
        Bag<DirectedEdge> b = new Bag<DirectedEdge>();
        for (int v = 0; v < V; v++) {
            for (DirectedEdge w : adj[v]) {
                b.add(w);
            }
        }
        return b;
    }
}

最短路径

在加权有向图中计算最短路径时，会用到一个由DirectedEdge对象组成的数组edgeTo[]和一个double类型的数组distTo[]。

• edgeTo表示了一颗最短路径树，保存的是算法的计算结果。以s为起点的一颗最短路径树是图的一副子图，它包含了s和从s可达的所有顶点。这棵树的根节点为s，树的每条路径都是有向图中的一条最短路径。
  edgeTo的索引表示图的结点，edgeTo[4]的值为指向结点4的边，这条边的to=4，from=指向结点4的顶点，weight=边的权重。
  根据edgeTo可沿着最短路径树不断上溯，直到树的根结点s。edgeTo[s]的值为null。

• distTo[]存储了从一个结点到达起点s的最短路径的成本。所以distTo[s]=0，并约定对于和s没有连通的结点，在distTo中对应位置的值为Double.POSITIVE_INFINITY，这样判断distTo某个位置是否等于Double.POSITIVE_INFINITY就可以知道它与s是否连通。

边的松弛

最短路径算法的实现基于一种叫做松弛(relaxation)的简单操作。一开始只知道图的边和它们的权重，distTo[]中只有起点所对应元素的值为0，其余元素的值都被初始化为Double.POSITIVE_INFINITY，随着算法的执行，它将起点到其他顶点的最短路径信息存入了edgeTo[]和distTo[]。在遇到新的边时，会通过松弛操作来更新最短路径。松弛操作是指对于边v->w，会检查从s到w的最短路径是否经过v，既s->v->w，如果是，就更新edgeTo[w]和distTo[w]，否则保持现状。

if (distTo[w] > distTo[v] + e.weight()) {
	distTo[w] = distTo[v] + e.weight();
	edgeTo[w] = e;
}

松弛这个术语来自于用一根橡皮筋沿着连接两点的路径紧紧展开的比喻，松弛一条边就类似于将橡皮筋转移到一条更短的路径上，使橡皮筋相比之前要松弛。

在最短路径算法的实现中，会尝试松弛从一个顶点指出的所有边，如果某次松弛操作改变了distTo和edgeTo的值，则这次操作是成功的，最终会找出到达每个顶点的最短路径。

Dijkstra算法

Dijkstra算法是基于上述讨论实现的，除了distTo和edgeTo数组之外，还需要一条索引优先队列（IndexMinPQ），以保存需要被松弛的顶点并确认下一个被松弛的顶点。IndexMinPQ除了具有MinPQ的功能，还可以通过索引修改对应位置的值，算法会利用IndexMinPQ将顶点v和distTo[v]关联起来，并在松弛操作中根据索引设置对应的路径距离。

public class DijkstraSP {
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    private IndexMinPQ<Double> pq;
    int s;

    public DijkstraSP(EdgeWeightedDigraph G, int s) {
        edgeTo = new DirectedEdge[G.V()];
        distTo = new double[G.V()];
        pq = new IndexMinPQ<Double>(G.V());
        this.s = s;

        for (int v = 0; v < G.V(); v++) {
            distTo[v] = Double.POSITIVE_INFINITY;
        }

        distTo[s] = 0.0;
        pq.insert(s, 0.0);
        while (!pq.isEmpty()) {
            relax(G, pq.delMin());
        }
    }

    private void relax(EdgeWeightedDigraph G, int v) {
        for (DirectedEdge e : G.adj(v)) {
            int w = e.to();
            if (distTo[w] > distTo[v] + e.weight()) {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
                if (pq.contains(w))
                    pq.change(w, distTo[w]);
                else
                    pq.insert(w, distTo[w]);
            }
        }
    }

    public double distTo(int w) {
        return distTo[w];
    }

    public boolean hasPathTo(int w) {
        return distTo(w) < Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v) {
        if (!hasPathTo(v))
            return null;

        Stack<DirectedEdge> path = new Stack<DirectedEdge>();
        for (DirectedEdge a = edgeTo[v]; a != null; a = edgeTo[a.from()]) {
            path.push(a);
        }
        return path;
    }

    // cmd /c --% java algs4.four.DijkstraSP ..\..\..\algs4-data\tinyEWG.txt
    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedDigraph ewdg = new EdgeWeightedDigraph(in);
        int s = Integer.parseInt(args[1]);
        DijkstraSP dijkstraSP = new DijkstraSP(ewdg, s);

        for (int t = 0; t < ewdg.V(); t++) {
            StdOut.print(s + " to " + t);
            StdOut.printf(" (%4.2f): ", dijkstraSP.distTo(t));
            if (dijkstraSP.hasPathTo(t)) {
                for (DirectedEdge e : dijkstraSP.pathTo(t)) {
                    StdOut.print(e + " ");
                }
            }
            StdOut.println();
        }
    }
}

8
16
4 5 0.35
4 7 0.37
5 7 0.28
0 7 0.16
1 5 0.32
0 4 0.38
2 3 0.17
1 7 0.19
0 2 0.26
1 2 0.36
1 3 0.29
2 7 0.34
6 2 0.40
3 6 0.52
6 0 0.58
6 4 0.93

对于上面tinyEWG.txt的内容所指定的图，如果要计算各点到起点0的最短路径，算法的执行轨迹为：

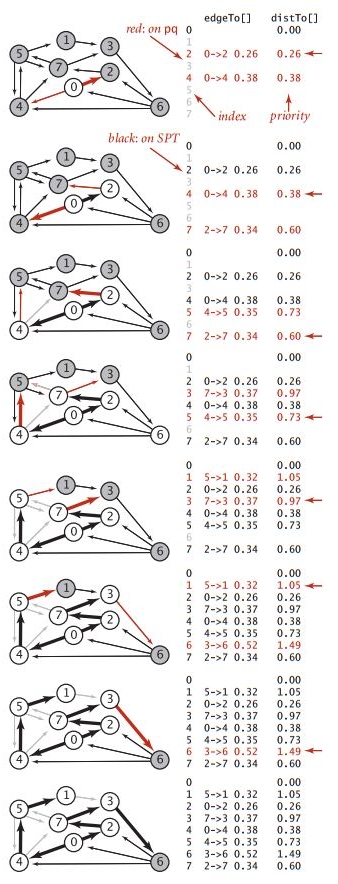
• 将顶点0加入优先队列，松弛以顶点0为起点的边，将从0指向的顶点2和4加入优先队列，将边0_>2和0->4添加到树中；
• 从优先队列删除顶点2，将2->7添加到树中，将顶点7加入优先队列；
• 从优先队列删除顶点4，将4->5添加到树中，但因为4->7松弛失败，这条边失效，将顶点5加入优先队列；
• 从优先队列删除顶点7，将7->3添加到树中，7->5松弛失败，将顶点3加入优先队列；
• 从优先队列删除顶点5，将5->1添加到树中，5->7松弛失败，将顶点5加入优先队列；
• 从优先队列删除顶点3，将3->6添加到树中，将顶点6加入优先队列；
• 从优先队列删除顶点6，优先队列为空，执行完毕。