【c++】R-K法求解常微分方程

最常用：四阶龙格库塔方法

　　　　　　　　　　

 

　　　　　　　　 

 

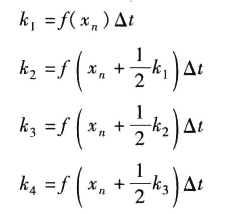
 例：

 

 

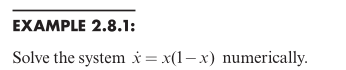
#include <iostream>
#include <fstream>
#include <cstring>

double func(double x) {
    return x * (1 - x);
}

void RK(double x0,double x[20]) {
    double dt{ 0.1 };
    double k1, k2, k3, k4;
    int count{ 0 };
    int flag{ 0 };
    for (int count{ 0 };count < 100;++count) {
        if (count % 5 == 0) {
            flag = count / 5;
            x[flag] = x0;
        }
        k1 = func(x0) * dt;
        k2 = func(x0 + 0.5 * k1) * dt;
        k3 = func(x0 + 0.5 * k2) * dt;
        k4 = func(x0 + 0.5 * k3) * dt;
        x0 += (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4);

    }
}

void show(double* x, int num) {
    for (int i = 0;i < num;i++) {
        std::cout << x[i] << '\n';
    }
}

void savetxt(double* x,int num,std::string name) {
    std::ofstream write;
    write.open(name,std::ostream::app); //以添加模式打开文件
    for (int i = 0;i < num;i++) {
        write << x[i] << '\n';
    }
    write.close();
}



int main()
{
    double x[20]{};
    RK(0.5,x);
    //show(x, 20);
    savetxt(x, 20, "k2.txt");
   RK(1.0, x);
    savetxt(x, 20, "K.txt");
    RK(0.2, x);
    savetxt(x, 20, "less than k2.txt");
    RK(0.8, x);
    savetxt(x, 20, "more than k2.txt");
    RK(1.5, x);
    savetxt(x, 20, "more than k.txt");
}

 

使用vector：

/*
    x0:初值
    dt：步长
    D：总时长
    p：控制输出的数量
*/
vecRow RK2(double x0,double dt,int D,int p) {
    double k1, k2, k3, k4;
    int count{ 0 };
    int flag{ 0 };
    int t{ static_cast<int>(D / dt) };
    int num{ static_cast<int>(t / p) };
    vecRow x(num);
    for (int count{ 0 };count < t;++count) {
        if (count % 5 == 0) {
            flag = count / p;
            x[flag] = x0;
        }
        k1 = func(x0) * dt;
        k2 = func(x0 + 0.5 * k1) * dt;
        k3 = func(x0 + 0.5 * k2) * dt;
        k4 = func(x0 + 0.5 * k3) * dt;
        x0 += (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4);
    }
    return x;
}