【c++】多项式曲线拟合

源代码，截取至数值分析期末大作业。其中一步为多项式曲线拟合，求解出符合拟合精度的函数表达式。

拟合和插值的区别？

　　1.拟合：不必经过所有点

　　2.插值：必须经过所有点

（1）曲线拟合

　　

 

 （2）误差的计算

　　　　　

 

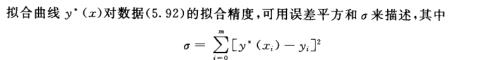
 （3）多项式曲线拟合

　　　　

 

　　　　 

 

 步骤：

　　1.设定k阶多项式

　　2.计算A^TAc^*=A^Ty ，得出c^*

　　3.计算误差，满足要求停止计算

（4）方便理解的例题

　　　　

 （5）代码计算使用的例题：

　　　　　　　　

int NUM;
void qxnh(double c_final[100]) {
    double x[21][21];
    double x_list[21] = { 0.000000,0.3149803,0.9999999,1.9655560,3.1748020,4.6050390,6.2402510,
                     8.068264,10.07937,12.26556,14.62009,17.13712,19.81156,22.63891,
                     25.61514,28.73660,31.99999,35.40231,38.94074,42.61273,46.41589 };
    for (int i = 0;i < 21;i++) {
        x[i][0] = x_list[i];
    }
    
    double y[21][21];
    for (int i = 0;i < 21;i++) {
        y[i][0] = 0.5 * i;
    }
    //k次多项式进行拟合 x=φ(y)
    double A[21][21];
    double AT[21][21];
    double ATA[21][21];
    double ATx[21][21];
    double ATA_1[21][21];
    double c[100];
    double new_x[21];
    double epsilon ;
    double new_ATx[21];
    double c_mul[21][21];
    for (int k = 0;k < 21;k++) {
        //int k = 5;
        for (int i = 0;i < 21;i++) {
            for (int j = 0;j < k;j++) {
                A[i][j] = pow(y[i][0], j);
            }
        }
        //求转置矩阵AT
        for (int i = 0;i < k;i++) {
            for (int j = 0;j < 21;j++) {
                AT[i][j] = A[j][i];
            }
        }
        //矩阵相乘 ATA
        multi(AT, A, k-1, 20, k,ATA);
        //矩阵相乘 ATy
        multi(AT, x, k-1, 20, 1, ATx);
        //求解逆矩阵(ATA)-1
        //inverse(ATA, k - 1, k - 1, ATA_1);
        //矩阵相乘 C=（ATA）-1ATy
        for (int i = 0;i < k;i++) {
            new_ATx[i] = ATx[i][0];
        }
        //multi(ATA_1, ATx, k-1, 20, 0, c_mul);
        //解方程
        equation_solver(ATA, new_ATx, c,k);
        //show(c, k, 1);
        double mid_y ;
        for (int i = 0;i < 21;i++) {
            mid_y = 0.0;
            for (int j = 0;j < k;j++) {
                mid_y += pow(y[i][0], j)*c[j];
            }
            new_x[i] = mid_y;
        }
        epsilon = 0.0;
        for (int i = 0;i < 21;i++) {
            epsilon += pow(new_x[i] - x[i][0], 2);
        }
        std::cout << "epsilon " <<k<<": "<< epsilon << "\n";
        if (epsilon <= 1e-6) {
            std::cout << "停止循环，此时k = " << k << ";多项式的阶数为："<<k-1<<'\n';
            NUM = k;
            for (int i = 0;i < k;i++) {
                c_final[i] = c[i];
            }
            break;
        }
    }

}

矩阵相乘：

void multi(double BT0[21][21], double B0[21][21], int m, int o, int n, double res[21][21]) {
    double BT[21][21];
    double B[21][21];
    double temp;
    for (int i = 0;i < 21;i++) {
        for (int j = 0;j < 21;j++) {
            BT[i][j] = BT0[i][j];
        }
    }
    for (int i = 0;i < 21;i++) {
        for (int j = 0;j < 21;j++) {
            B[i][j] = B0[i][j];
        }
    }
    for (int i = 0;i < m + 1;i++) {
        for (int j = 0;j < n + 1;j++) {
            temp = 0;
            for (int k = 0;k < o + 1;k++) {
                temp += BT[i][k] * B[k][j];
            }
            res[i][j] = temp;
        }
    }
    /*for (int i = 0;i < m + 1;i++) {
        for (int j = 0;j < n + 1;j++) {

            std::cout<<res[i][j]<<"   ";
        }
        std::cout << "\n";
    }*/
}

高斯法解方程：

void equation_solver(double dF_o[21][21], double F_o[21], double dx[100],int K) {
    int point = 0;
    double temp = 0.0;
    double dF[21][21];double F[21];

    //赋值
    for (int i = 0;i < K;i++) {
        for (int j = 0;j < K;j++) {
            dF[i][j] = dF_o[i][j];
        }
    }
    for (int i = 0;i < K;i++) {
        F[i] = F_o[i];
    }
    //选主元

    for (int k = 0;k < K-1;k++) {
        point = k;
        for (int l = k;l < K;l++) {
            if (fabs(dF[point][k]) < fabs(dF[l][k])) {
                point = l;
            }
        }
        //换行
        temp = 0;
        temp = F[point];
        F[point] = F[k];
        F[k] = temp;
        for (int l = k;l < K;l++) {
            temp = 0;
            temp = dF[point][l];
            dF[point][l] = dF[k][l];
            dF[k][l] = temp;
        }
        //消去过程
        double mid;
        for (int l = k + 1;l < K;l++) {
            mid = dF[l][k] / dF[k][k];
            F[l] = F[l] - mid * F[k];
            for (int p = 0;p < K;p++) {
                dF[l][p] -= mid * dF[k][p];
            }
        }
    }
   /* std::cout << "上三角： " << '\n';
    for (int i = 0;i < 4;i++) {
        for (int j = 0;j < 4;j++) {
            std::cout << "i" << i << "j" << j << "  " << dF[i][j] << "  ";
        }
        std::cout << "\n";
    }*/

    //求解方程
    int M = K - 1;
    dx[M] =F[M] / dF[M][M];
    for (int i = K-2;i > -1;i--) {
        temp = 0;
        //dx[i] = 0;
        for (int j = i + 1;j < K;j++) {
            temp += dF[i][j] * dx[j] / dF[i][i];
            //dx[i] -= dF[i][j] * dx[j] / dF[i][i];
        }
       dx[i] = F[i] / dF[i][i] - temp;
        //std::cout << "dx" << i << ": " << dx[i] << "\n";
    }

}

point1：更新矩阵乘法和解方程的代码。

详细见博客：

【c++】以函数调用的方式来书写矩阵乘法 - 致命一姬 - 博客园 (cnblogs.com)

【c++】列主元素高斯消去法求解方程 - 致命一姬 - 博客园 (cnblogs.com)

point2：避免全局变量NUM的使用

point3：使用函数重载来解决不同矩阵对矩阵乘法的需求

最后实现计算多项式曲线拟合的代码如下：

#include <iostream>
#include <vector>
#include <cassert>
#include <math.h>

using vec = std::vector<std::vector<double>>;
using vecRow = std::vector<double>;

vec multi(vec A, vec B) {
    int row1{ static_cast<int> (A.size()) };
    int col1{ static_cast<int>(A[0].size()) };
    int row2{ static_cast<int>(B.size()) };
    int col2{ static_cast<int>(B[0].size() )};
    vec res(row1, vecRow(col2));
    double temp{};
    assert(col1 == row2 && "第一个矩阵的列和第二个矩阵的行不相等");
    for (int i = 0;i != row1;++i) {
        for (int j = 0;j != col2;++j) {
            temp = 0;
            for (int k = 0;k != col1;++k) {
                temp += A[i][k] * B[k][j];
            }
            res[i][j] = temp;
        }
    }
    return res;
}

vecRow multi(vec A, vecRow B) {
    int row1{ static_cast<int> (A.size()) };
    int col1{ static_cast<int>(A[0].size()) };
    int row2{ static_cast<int>(B.size()) };
    int col2{ 1 };
    vecRow res(row1);
    double temp{};
    assert(col1 == row2 && "第一个矩阵的列和第二个矩阵的行不相等");
    for (int i = 0;i != row1;++i) {
        temp = 0;
        for (int j = 0;j != row2;++j) {
            temp += A[i][j] * B[j];
        }
        res[i] = temp;
    }
    return res;
}



vecRow equationSolver(vec A, vecRow B) {   //如果这里为vec&A vecRow&B ，则A和B的值会改变。如果没有&，则不变，改变的为A和B的副本
    int row1{ static_cast<int> (A.size()) };
    int col1{ static_cast<int>(A[0].size()) };
    int row2{ static_cast<int>(B.size()) };
    assert((row1 == row2) || (row1 > 0) && "请检查输入");
    int point;
    double temp;
    double m;
    vecRow x(row1);
    if (row1 == 1) {
        x[row1] = B[row1] / A[row1][row1];
        return x;
    }
    //一列一列来
    for (int k = 0;k != col1 - 1;++k) {
        //选主元
        point = k;
        //寻找k列中绝对值最大的数的行point
        for (int r = k;r != row1;++r) {
            if (fabs(A[point][k]) < fabs(A[r][k])) {
                point = r;
            }
        }
        //判断A是否为奇异矩阵
        assert(fabs(A[point][k]) > 1e-6 && "A为奇异矩阵");
        //换行
        temp = B[k];
        B[k] = B[point];
        B[point] = temp;
        for (int i = 0;i != col1;++i) {
            temp = A[point][i];
            A[point][i] = A[k][i];
            A[k][i] = temp;
        }
        //消去
        m = 0.0;
        for (int i = k + 1;i != col1;++i) {
            m = A[i][k] / A[k][k];
            B[i] -= m * B[k];
            for (int j = 0;j != col1;++j) {
                A[i][j] -= m * A[k][j];
            }
        }
    }
    //解方程
    double sum{ 0.0 };
    x[row1 - 1] = B[row1 - 1] / A[row1 - 1][row1 - 1];
    for (int i = row1 - 2;i >= 0;--i) {
        sum = 0.0;
        for (int j = i + 1;j != col1;++j) {
            sum += A[i][j] * x[j] / A[i][i];
        }
        x[i] = B[i] / A[i][i] - sum;
    }
    /*for (double i : x) {
        std::cout << i << "  ";
    }*/
    return x;
}


//计算转置矩阵
vec transpose(vec A) {
    int row{ static_cast<int> (A.size()) };
    int col{ static_cast<int>(A[0].size()) };
    vec B(col, vecRow(row));
    for (int i = 0;i != row;++i) {
        for (int j = 0;j != col;++j) {
            B[j][i] = A[i][j];
        }
    }
    return B;
}

//计算多项式拟合的结果
vecRow compute(vecRow c, vecRow y) {
    int row_c{ static_cast<int> (c.size()) };
    int row_y{ static_cast<int> (y.size()) };
    double temp{};
    vecRow result(row_y);
    for (int i = 0;i != row_y;++i) {
        temp = 0.0;
        for (int j = 0;j != row_c;++j) {
            temp += pow(y[i], j)*c[j];
        }
        result[i] = temp;
    }
    return result;
}


//计算误差
double epsilon(vecRow A, vecRow B) {
    int row_A{ static_cast<int> (A.size()) };
    int row_B{ static_cast<int> (B.size()) };
    assert(row_A == row_B, "please check the input");
    double mid{};
    for (int i = 0;i != row_A;++i) {
        mid += pow(A[i] - B[i], 2);
    }
    return mid;
}

//返回方程求解的结果vecRow c，然后具体的k可以通过计算c的大小得出
//传入x=φ(y)的x和y
vecRow qxnh(vecRow x,vecRow y) {
    int k{ 2 };
    int row_x{ static_cast<int> (x.size()) };
    int row_y{ static_cast<int> (y.size()) };
    assert(row_x == row_y, "please check the input");
    double ep{};
    vecRow result(row_x);
    while (1) {
        //构建A
        vec A(row_x, vecRow(k));
        for (int i = 0;i!= row_y;++i) {
            for (int j = 0;j != k;++j) {
                A[i][j] = pow(y[i], j);
            }
        }
        vec AT{ transpose(A) };
        //ATA
        vec ATA{ multi(AT,A) };
        //ATy,该例中，y为x。函数重载
        vecRow ATy{ multi(AT, x) };
        vecRow c{ equationSolver(ATA,ATy) };
        result = compute(c, y);
        ep = epsilon(result, x);
        if (ep <= 1e-6) {
            std::cout << "停止循环，此时k = " << k << ";多项式的阶数为：" << k - 1 << '\n';
            return c;
        }
        else {
            ++k;
        }
    }
}

void show(vec A) {
    for (vecRow i : A) {
        for (double j : i) {
            std::cout << j << " ";
        }
        std::cout << '\n';
    }
}

void show(vecRow A) {
    for (double i : A) {
        std::cout << i << " ";
        std::cout << '\n';
    }
}


int main()
{
    vecRow x{ 0.000000,0.3149803,0.9999999,1.9655560,3.1748020,4.6050390,6.2402510,
                     8.068264,10.07937,12.26556,14.62009,17.13712,19.81156,22.63891,
                     25.61514,28.73660,31.99999,35.40231,38.94074,42.61273,46.41589 };
    //int k ;
    int row_x{ static_cast<int> (x.size() )};
    vecRow y(row_x);
    for (int i = 0;i != row_x;++i) {
        y[i] = 0.5 * i;
    }
    qxnh(x,y);
}