初探Floyd和Dijkstra

Floyd：

问题：Floyd算法求解下图各个顶点的最短距离

 

 

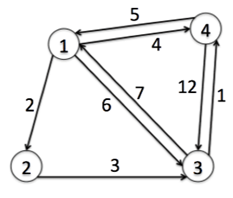
解析：

从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，算法假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，算法检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离

 

核心代码：

for(u = 0; u < G.vexnum; ++ u)
    for(v = 0; v < G.vexnum; ++ v)
        for(w = 0; w < G.vexnum; ++ w)
            if(D[v][u] + D[u][w] < D[v][w])// 从v经u到w的一条路径更短
                D[v][w] = D[v][u] + D[u][w];

 

代码：

 

#include<bits/stdc++.h>
using namespace std;
int main() {
    int e[10][10],k,i,j;
    int inf=0x3f3f3f3f;
    for(i=1; i<=4; i++)
        for(j=1; j<=4; j++)
            if(i==j) e[i][j]=0;
            else e[i][j]=inf;
    e[1][2] = 2, e[1][3] = 6, e[1][4] = 4;
    e[2][3] = 3;
    e[3][1] = 7, e[3][4] = 1;
    e[4][1] = 5, e[4][3] = 12;
    //Floyd-Warshall算法核心语句
    for(k=1; k<=4; k++)
        for(i=1; i<=4; i++)
            for(j=1; j<=4; j++)
                if(e[i][j]>e[i][k]+e[k][j] )
                    e[i][j]=e[i][k]+e[k][j];
    //输出最终的结果
    for(i=1; i<=4; i++) {
        for(j=1; j<=4; j++) {
            printf("%d ",e[i][j]);
        }
        printf("\n");
    }
    return 0;
}

 

Dijkstra：

问题：用Dijkstra算法求由顶点a到顶点b的最短路径

 

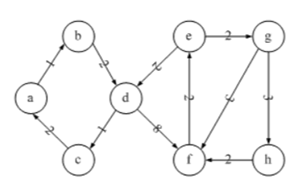
解析：

①    不断运行广度优先算法找可见点，计算可见点到源点的距离长度

②    从当前已知的路径中选择长度最短的将其顶点加入S作为确定找到的最短路径的顶点。

	a	b	c	d	e	f	g	h
A	0	1	2	∞	∞	∞	∞	∞
B	∞	0	∞	2	∞	∞	∞	∞
C	2	∞	0	∞	∞	∞	∞	∞
D	∞	∞	1	0	∞	8	∞	∞
E	∞	∞	∞	2	0	∞	2	∞
F	∞	∞	∞	∞	2	0	∞	∞
G	∞	∞	∞	∞	∞	3	0	3
h	∞	∞	∞	∞	∞	2	∞	0

 代码：

#include<bits/stdc++.h>
using namespace std;

const int inf = 0x3f3f3f3f;
int edge[9][9] ={
    {-1, -1, -1, -1, -1, -1, -1, -1, -1},
    {-1,  0,  1,inf,inf,inf,inf,inf,inf},
    {-1,inf,  0,inf,  2,inf,inf,inf,inf},
    {-1,  2,inf,  0,inf,inf,inf,inf,inf},
    {-1,inf,inf,  1,  0,inf,  8,inf,inf},
    {-1,inf,inf,inf,  2,  0,inf,  2,inf},
    {-1,inf,inf,inf,inf,  2,  0,inf,inf},
    {-1,inf,inf,inf,inf,inf,  3,  0,  3},
    {-1,inf,inf,inf,inf,inf,  3,inf,  0}
};
int main() {
    const int n = 8;//点的数量
    int dis[n+1];//当前各点到源点的距离
    int book[n+1];//各点到源点是否为最小值
 
    //初始化，设源点为n1
    for (int i = 1; i <= n; ++i)
        dis[i] = edge[1][i];
 
    //book数组初始化
    memset(book, 0, sizeof(book));
    book[1] = 1;
 
    int min;//当前，未确定最短路径的点，到源点的最小距离大小
    //Dijkstra算法核心语句
    for (int i = 1; i <= n - 1; ++i) {
        //找到离1号顶点最近的顶点
        min = inf;
        int u;
        for (int j = 1; j <= n; ++j) {
            if (book[j] == 0 && dis[j] < min) {
                min = dis[j];
                u = j;
            }
        }
        //每轮迭代都可以确定一个点到源点的最短距离，因此只要迭代n-1轮
        book[u] = 1;
        //通过已经确定的点，对dis数组进行更新
        //（未确定的点通过点u，缩小了到源点的距离）
        for (int v = 1; v <= n; ++v) {
            if (edge[u][v] < inf) {
                if (dis[v] > dis[u] + edge[u][v])
                    dis[v] = dis[u] + edge[u][v];
            }
        }
    }
    //输出结果
    for (int i = 1; i <= n; ++i) cout << dis[i] << ' ';
    return 0;
}