算法面试简单小结

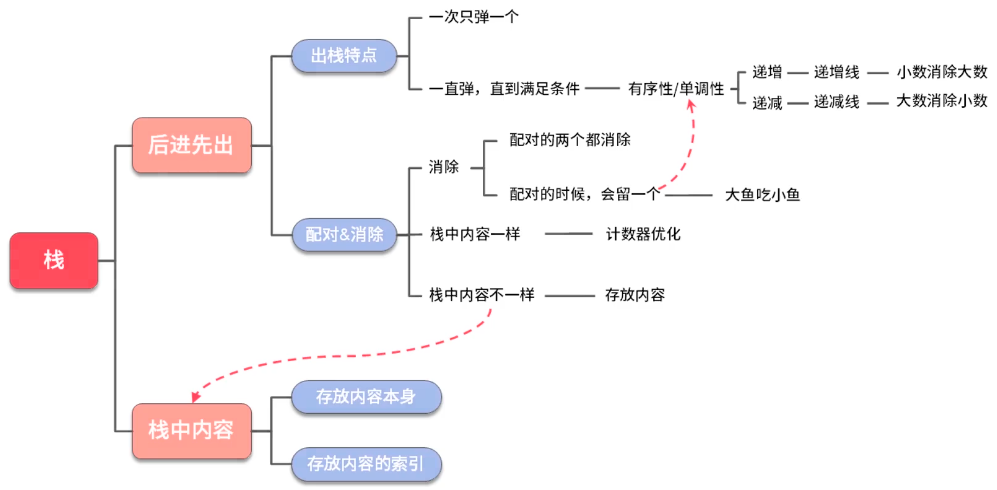
栈

1. 题括号匹配
2. 大鱼吃小鱼
3. 单调栈：题 找到一个数组中每个元素的右边第一个比它小的元素的位置
4. 单调栈 + 元素个数限制
5. 最大矩形面积问题——单调栈法-CSDN博客

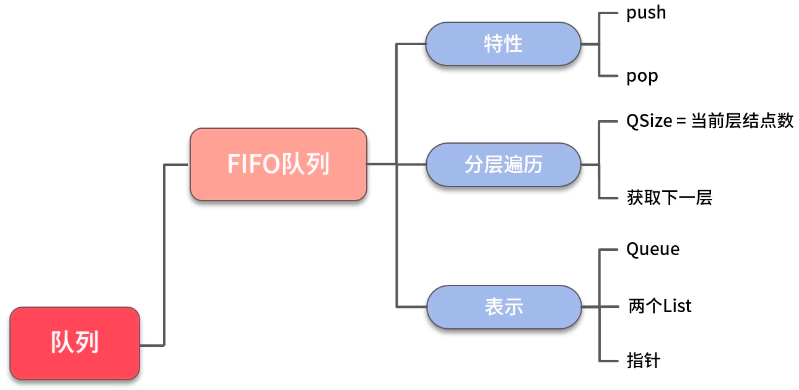
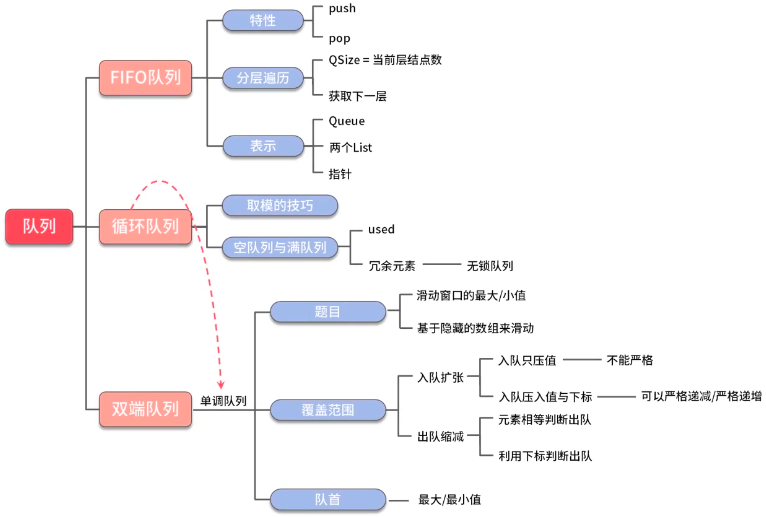
队列

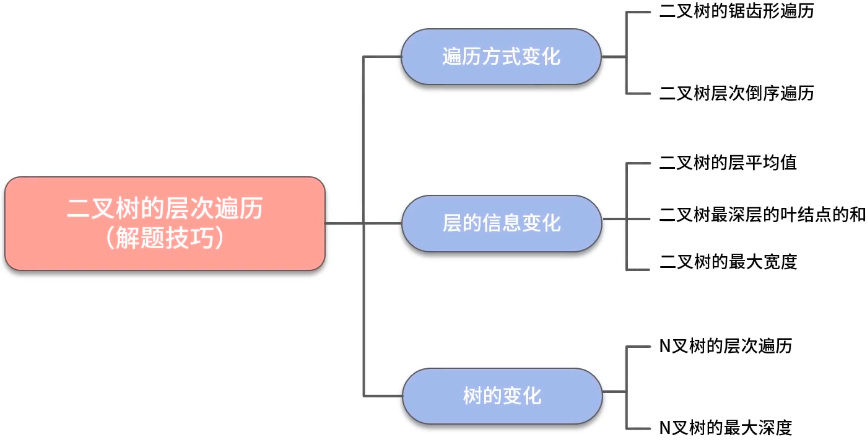
1. 二叉树层序遍历
2. 单调队列
3. 单调队列 - 捡金币

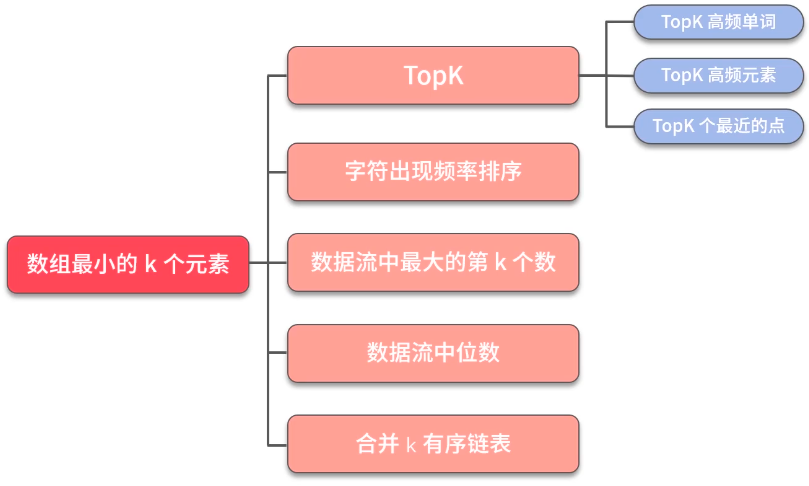
优先级队列 堆

1. 数组TopK大小元素，也可用快排解决

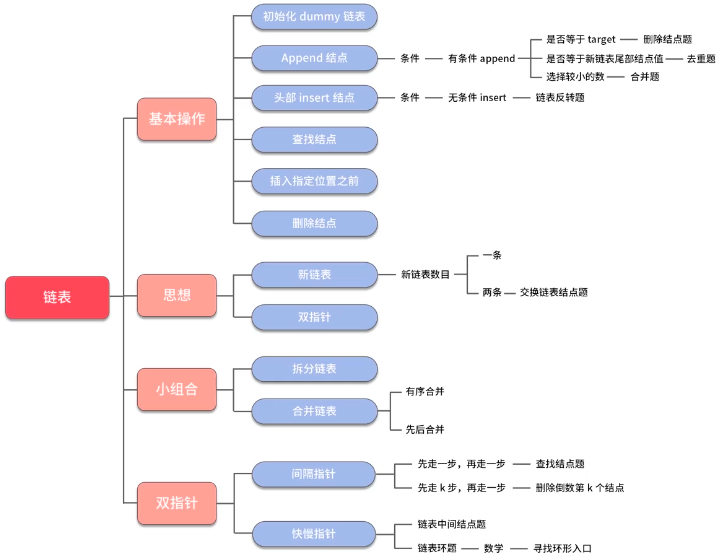
链表

方法：假头、新链表、双指针（间隔指针、快慢指针）

 

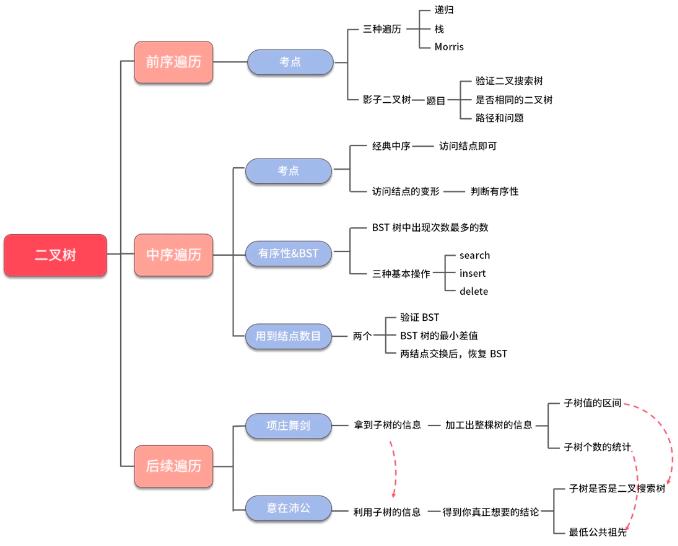
二叉树

• 前序遍历：将树根信息传递给子树
• 中序遍历：有序性
• 后序遍历：将子树信息传递给树根

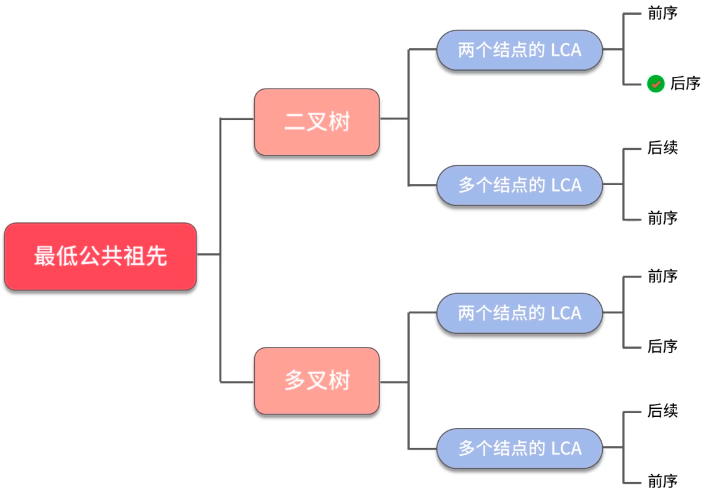
双指针

要求数据具有单调性，例如子序列的和随着长度的增加是单调增加还是会增或减；无重复子序列随着长度增长可能变得有重复、但有重复子序列不会变为无重复子序列。

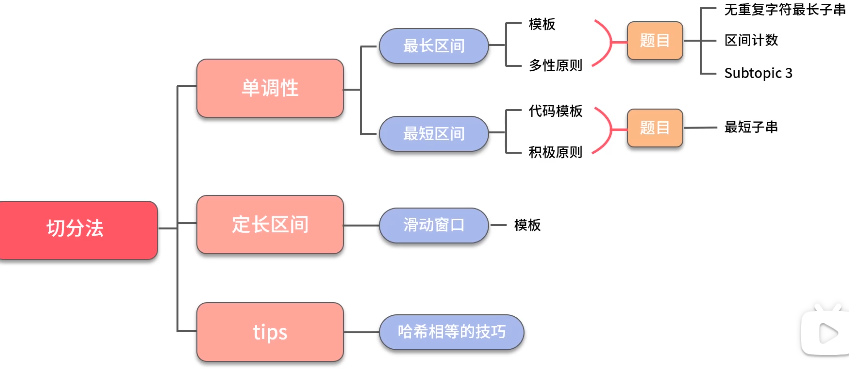
双指针模板

 // 最长区间
int maxLength(int[] A) {
    int N = A.length; // 区间左指针
    int left = -1;
    int ans = 0;
    for (int i = 0; i < N; i++) {
        // 判断在加入 A[i] 前，(left, i-1]是一个有效区间
        // 直接将 A[i] 加入区间，形成 (left, i]
        // 将 A[i] 加入后，惰性原则
        while (check((left, i])) { // 检查区间状态是否满足条件
            ++left; // 如果不满足，移动左指针
            // 修改区间装填
        }
        // 此时区间 (left, i] 满足条件
        ans = max(ans, i - left);
    }
    return ans; // 返回最优解
}

// 定长区间
int fixedLength(int[] A, int windowsSize) {
    final int N = A== null ? 0 : A.length;
    int left = -1;
    for (int i = 0; i < N; i++) {
        // step 1 将A[i]加入区间，形成 (left, i]
        // TODO 修改区间状态

        // 如果滑动窗口太小
        if (i - left < windowsSize) {
            continue;
        }
        // 此时 (left, i] 长度必然等于 windowSize
        // TODO 判断区间状态是否满足约束条件
        left++;
        // step 2 移除 A[left]
        // TODO 修改区间状态
    }
    return ans; // 返回最优解
}

// 最短区间
int minimalRange(int[] A) {
    final int N = A== null ? 0 : A.length;
    int left = -1; // 开闭区间的左侧
    int ans = A.length + 1; // 记录最短子串长度
    for (int i = 0; i < N; i++) {
        // 注意在加入 A[i] 前，(left, i-1] 可能不满足条件
        // step 1 直接将 A[i] 加入区间
        // step 2 TODO 更新区间
        while (区间超出/满足条件) {
            ans = Math.min(ans, i - left);
            // step 3 移除 A[++left]
            // step 4 TODO 更新区间状态
        }
        // 区间 (left, i] 在此处肯定不满足条件
    }
    return ans;
}

 

贪心算法

特点：

• 每次抛弃局部次优解，只选局部最优解
• 不能“逆袭”“反向”，次优解不会在下一个阶段变为最优解
• 没有固定模板，一般依赖现有结论

排序

二分查找

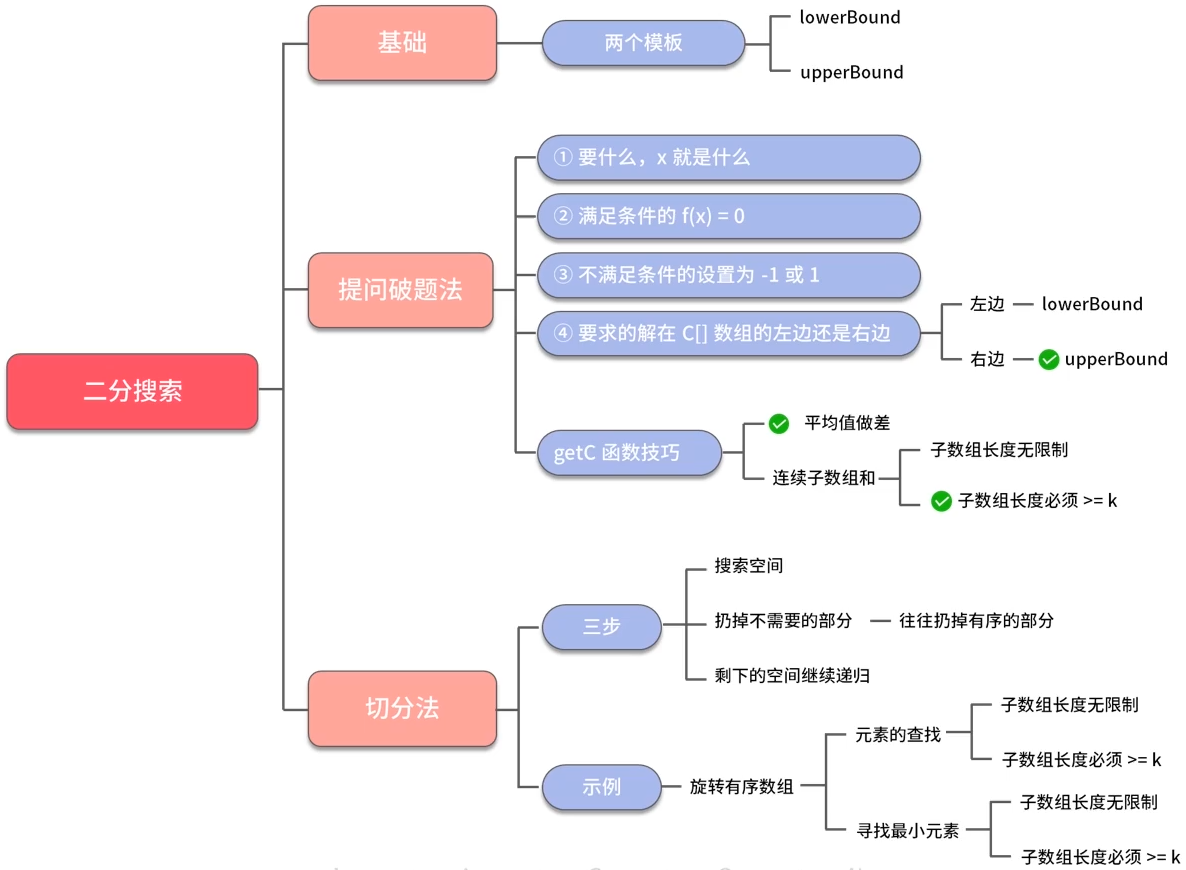
lowerBound upperBound 用于查找符合条件的最左或右的元素（区间左闭右开）

lowerBound upperBound

int lowerBound(long[] A, int n, long target) {
    int l = 0, r = n;
    while (l < r) {
        final int m = l + ((r - l) >> 1);
        if (A[m] < target) {
            l = m + 1;
        } else {
            r = m;
        }
    }
    return l;
}
int upperBound(long[] A, int n, long target) {
    int l = 0, r = n;
    while (l < r) {
        final int m = l + ((r - l) >> 1);
        if (A[m] <= target) {  // <=========== 差异在于等于号
            l = m + 1;
        } else {
            r = m;
        }
    }
    return l;
}

回溯

特点：有借有还

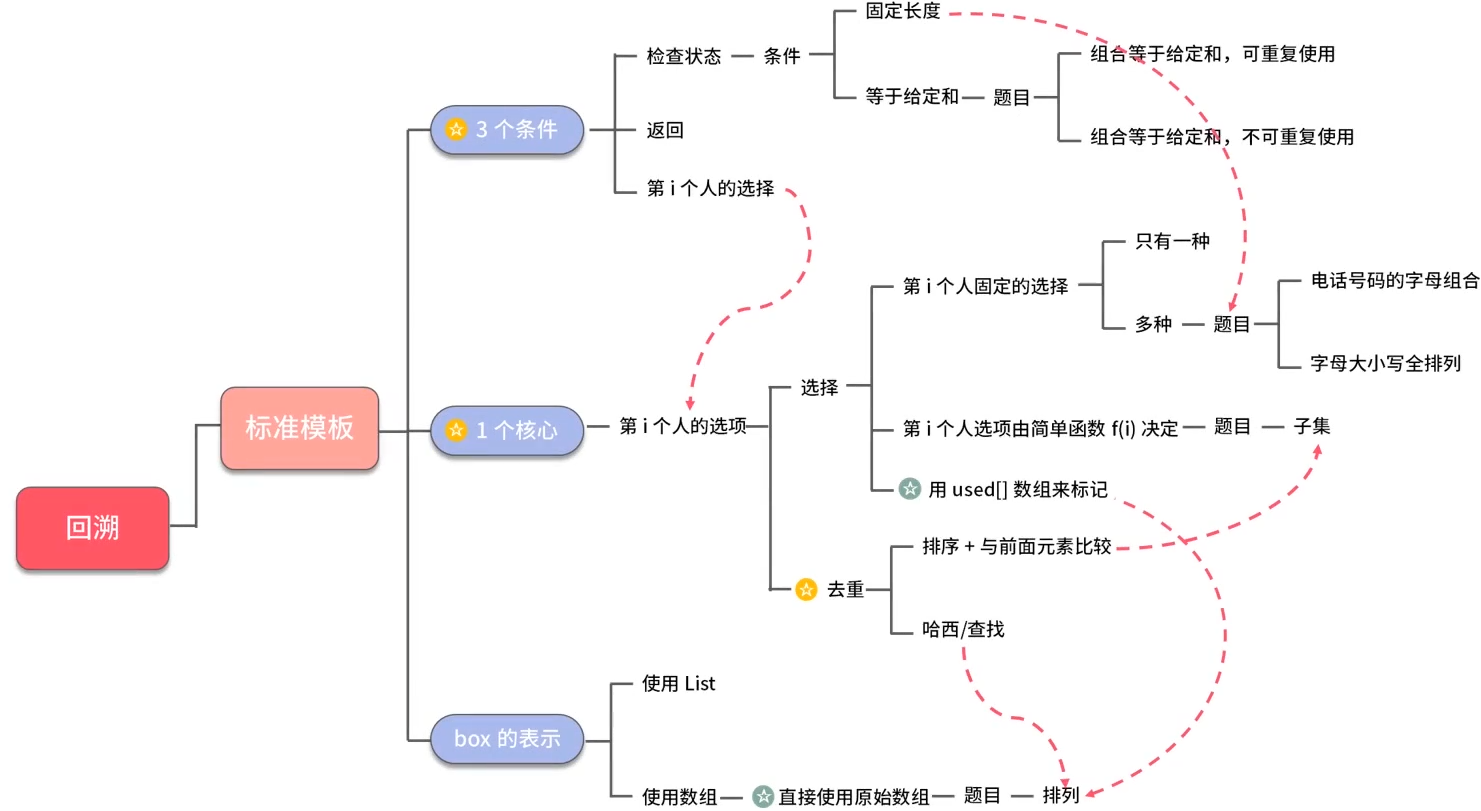
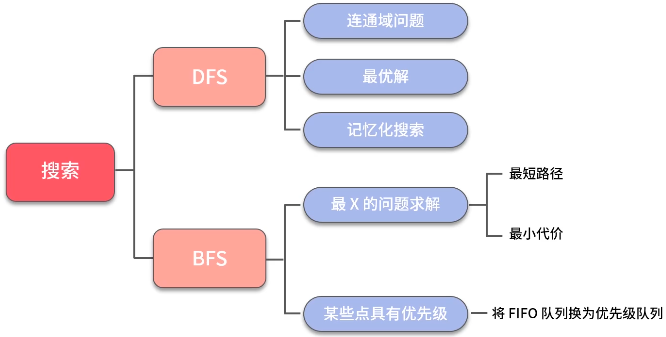
搜索

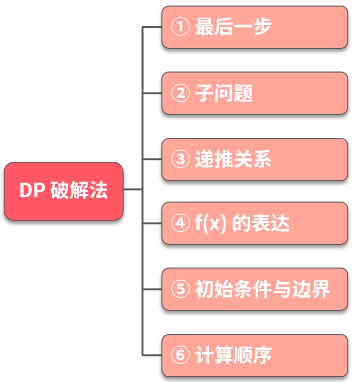
动态规划

特点：

1. 计数：有多少种方法
2. 最值：最大子序列、最小实践、最少操作次数
3. 可能性：能否满足某种情况

dp题目需要“逆向思维”，从后向前思考，而非简单的模拟

初始条件：结果本身的存放不越界，计算过程中越界，如 dp[0] dp[1]
边界：结果本身的存放就是越界的，如 dp[-1]

题目类型：

1. 线性dp
2. 区间dp
3. 背包dp
4. 树形dp
5. 状态压缩dp