读---白话大数据与机器学习

第二章 步入数据之门

什么是数据

承载了信息的东西

什么是信息

信息是用来消除随机不定性的东西

 算法

在同一个算 法中，不同的参数和阈值设置同样会带来大相径庭的结果，甚至影响数据解读的科学性

第三章 排列组合与古典概型

1.古典概型

如果一个随机试验所包含的单位事件（就是刚才说的3次朝上分别为“正正正”、“正正

反”……这其中每一种情况都是单位事件）是有限的，且每个单位事件发生的可能性均相

等，则这个随机试验叫做拉普拉斯试验，这种条件下的概率模型就叫古典概型。古典概型也

叫传统概率，该定义是由法国著名数学家拉普拉斯（Laplace）提出的。

 

第4章 统计与分布

 

4.1.1 加和值

以使用加和值来对一群事物进行描述是一种非常自然的描述方式，比如：超市结账，使用加和值来对整体进行描述

 

 4.1.2 平均值

“一年级一班有40名学生，3门课程平均分为80分”。

“一年级二班有60名学生，3门课程平均分为75分”。

“一年级三班有50名学生，3门课程平均分为80分”。

从这组数据来看，基本可以得到一个印象，就是一年级一班的成绩“普遍”比一年级二

班“好”，至少是从“宏观体现”上看比二班好，它和一年级三班“一样好”。但是一年级一班和

一年级三班这两个班的每个人的成绩都是一样的吗？至少人数是不一样的。那么也许还需要

进一步地描述这平均下来的80分和每个学生具体的课程分数之间的差异性有多大，这就涉及

另一个描述的需求——标准差。

 

4.1.3 标准差

我们先上公式，标准差公式如下：

 

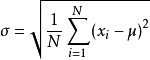
下面解释一下这个公式的含义。

我们以一年级一班所有40个学生为例，那么3门考试的情况下全班就有120个分数参与统

计，也就是n=120。把每个学生每门课的成绩减去全班的3个学科总的平均分80分，这样得到

120个差值，再把这些差值分别平方（主要是为了去掉负数，因为在分数差距里面，不管是

比这个平均值多，还是比这个平均值少，都被视为偏差），将这些平方的结果再加和，之后

除以参与统计的学科数量120，最后开平方，这个数字只可能是一个大于等于零的数字。用

汉字描述起来很啰嗦，但是一旦变成一个标准差的指标以后，由于是约定俗成的，所以只需

要“标准差”这3个字就能表示了。

这个数字表示的是什么含义？从这个数字得到的过程其实不难看出来。

如果所有的人的所有课程成绩都是和平均分一样，那么算出来的标准差就是0，因为每

一个 ( xi - u )^2  肯定都是0^2；反之，如果所有的人的课程成绩与平均分的差距都很大，

好的很好，差的很差，那么结果就是这个值会很大。如果一个班级成绩标准差比另一个班级

成绩的标准差小，说明学生之间的考试成绩水平差不多，标准差大则说明学生之间的考试成

绩水平相差比较大。

 

4.2 加权均值

如以重量1：4的原浆和水的比例来勾兑白酒，勾兑完的白

酒成本怎么计算？

1kg白酒成本=（1kg白酒原浆成本×1+1kg水成本×4）÷（1+4）

而绝对不会是

（1kg白酒原浆成本+1kg水成本）÷2

 

4.3.1 众数

我们可以感性地理解众数就是在样本对象中出现最多的那个数字

 

4.3.2 中位数

中位数，顾名思义，就是位于中间位置的数字

用中位数来描述样本的分布，在一定程度上可以消除个别极端值对整个样本平均值的影响。 

 

4.4 欧氏距离

这个距离需要用两个点在各自维度上的坐标相减，平方后相加然后再开平方

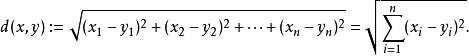
4.5 曼哈顿距离

d(i,j)=|X1-X2|+|Y1-Y2|.

在国际象棋棋盘上，有这种横平竖直的格子，描述格子和格子之间的距离可以直接用曼哈顿距离

 

第8章 回归

8.1 线性回归

 

回归的英文是Regression，单词原型的regress大概的意思是“回退，退化，倒退”。其实

Regression——回归分析的意思借用了“倒退，倒推”的含义。简单说就是“由果索因”的过

程，是一种归纳的思想——当看到大量的事实所呈现的样态，推断出原因是如何的；当看到

大量的数字对（pair）是某种样态，推断出它们之间蕴含的关系是如何的

 

线性回归是利用数理统计学中的回归分析来确定两种或两种以上变量间相互依赖的定量

关系的一种统计分析方法。其表达形式如下：

y = ax + b + e

e为误差服从均值为0的正态分布

 

8.2拟合

这种把平面上一系列的点用一条光滑的曲线连接起来的过程就叫做拟合

 

8.4 过拟合

过拟合简称“过拟”，是在拟合过程中出现的一种“做过头”的情况

 

过度拟合的危害有以下几点。

（1）描述复杂。所有的过度拟合的模型都有一个共同点，那就是模型的描述非常复杂

——参数繁多，计算逻辑多。

 

（2）失去泛化能力。所谓泛化能力就是通过学习（或机器学习）得到的模型对未知数

据的预测能力，即应用于其他非训练样本的向量时的分类能力。对于待分类样本向量分类正

确度高，表示泛化能力比较好；反之，如果对于待分类样本向量分类正确度低，则表示泛化

能力较差。

 

8.5 欠拟合

欠拟顾名思义，就是由于操作不当——也可以说建模不当产生的误差e分布太散或者太

大的情况。这种情况下，通常体现出来的都是在线性回归中的因素考虑不足的情况，常见的

原因有以下两种。

（1）参数过少   

对于训练样本向量的维度提取太少会导致模型描述的不准确。

例如，要根据银行储户的信息来判断其信誉好或不好，通常需要综合考虑用户的年龄、

流水总和、账户余额、借贷频次、借贷额度、归还准时程度等信息特征。这些因素考虑得越

充分，通常对于用户的信誉好或不好，给予的信用额度多少为宜就会有比较可靠的预测程

度。而如果参数太少，如只有账户余额一项，那么就不得不用账户余额一个参数和信誉好坏

去建立一个模型映射关系。这个模型是很不科学的，通过一个余额的数字就能断言一个人信

誉几何太过武断。

（2）拟合不当。拟合不当的原因比较复杂，通常是拟合方法不正确造成的。