知识点
循环不变量
用于证明迭代算法

例题:用循环不变量证明选择排序正确性
- 循环不变量:在第\(j\)次迭代执行前,\(A[1,2,...,j-1]\)已经有序
- 初始步:在第一次迭代之前,已排序的子序列为空,因此循环不变量成立。
- 归纳步:假设在第\(j=k\)个迭代前,\(A[1,2,..,k-1]\)有序。当执行迭代\(j=k\)时,从\(A[k,,,n]\)中选出最小的元素放在已排序序列的末尾,则在第\(k\)次迭代后,\(A[1,2,...,k]\)将包含第k个最小元素并且保证\(A[k-1]<=A[k]\),因此\(A[1,2,...,k]\)有序。
- 终止步:当\(j=n+1\)时,循环终止,此时\(A[1,2,...,n]\)有序,算法正确。
渐进符号
-
同阶、渐进紧界
- 定义

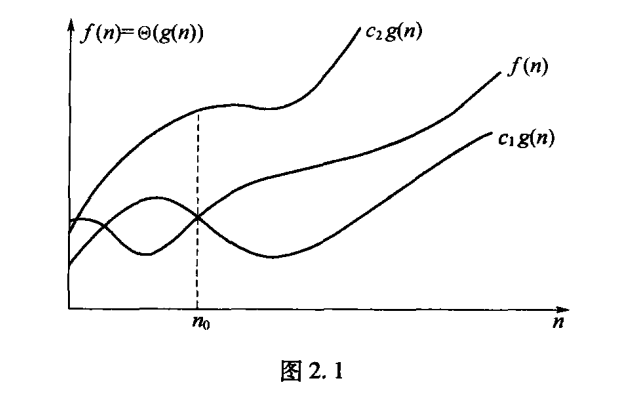
-
证明
-
定义

-
极限
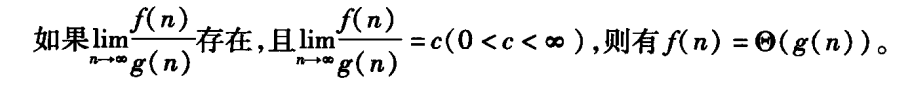
-
-
低阶、渐进上界
-
定义

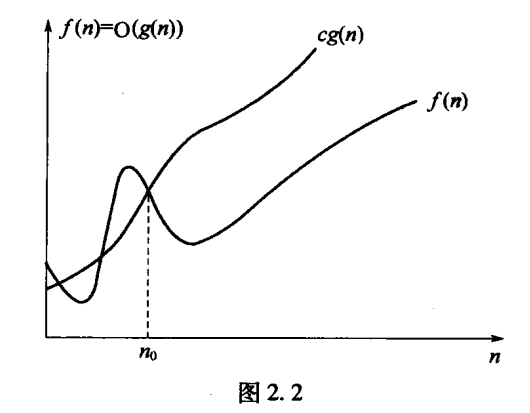
-
证明
-
定义
-
极限
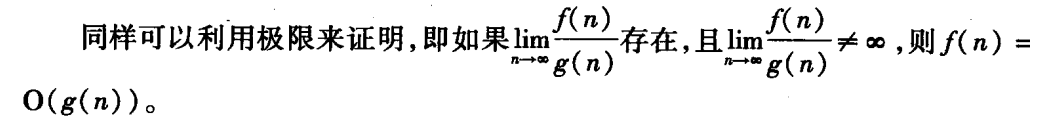
-
-
-
高阶、渐进下界
-
定义

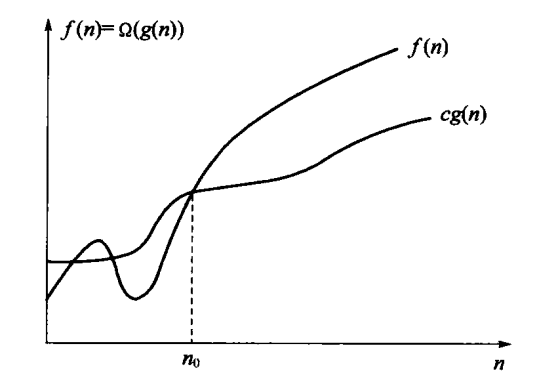
-
证明
-
定义
-
极限
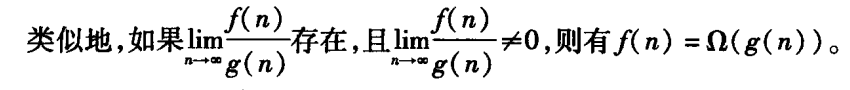
-
-
-
例题
-
相加取大

-
定理2.1
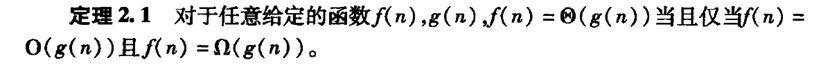

-
算法分析方法
概率分析
-
优点:概率分析基于概率论和随机性质,可以在平均情况下评估算法的性能。它考虑了输入的可能分布情况,对于涉及随机性的算法特别有用。
-
缺点:概率分析通常需要对输入的概率分布进行假设,并且在某些情况下可能难以准确估计概率。此外,它可能忽略最坏情况下的性能。
-
例子
-
线性搜索

-
插入排序
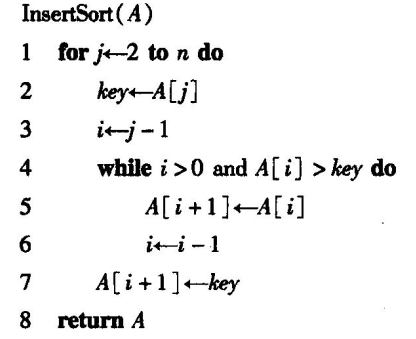
-
聘用秘书

-
分摊分析
-
优点:不需要复杂的概率分析且更符合实际情况,保证了最坏情形下每个运算的平均性能。
-
缺点:分摊分析假设每个操作的开销都是均摊到所有操作中的,但实际情况可能有所不同。对于特定输入,某些操作的实际开销可能会超过平均开销。
-
方法
-
合计方法:求出每一次运算的费用,加起来得到总费用关于\(n\)的表达式\(T(n)\),则分摊费用就是\(T(n)/n\)
-
记账方法:想出来要给每次运算分配的费用是多少,列出运算序列、分摊费用、实际费用、存款这四个数列,发现存款始终非负,则分摊费用就是想出来的那个
-
势能方法
-
重要不等式
\(\sum_{j=0}^{lgn}2^j=2n-1\)
-
-
例子
-
multipop

-
二进制累加

-
实验分析
- 优点:简单实用
- 缺点:容易受所选测试实例、计算模型、实验参数等的影响
递归
例子
-
计算\(2^k\)问题
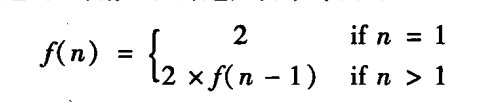
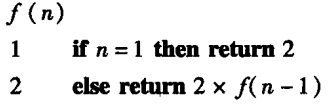

-
汉诺塔问题

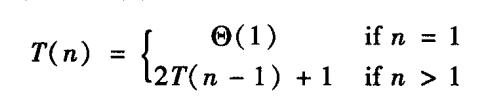
求时间复杂度就是把\(T(n)\)解出来,这里\(T(n)=O(2^n)\)
-
选择排序



-
排列问题
方法一:

方法二:

时间复杂度递推关系式:
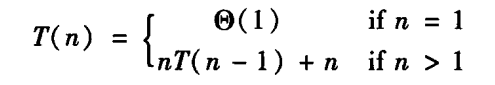
设计原则

公式法解递归方程

这里的结果是同阶(渐进紧界)的,用\(\Theta\)符号
动态规划
与分治的关系

装配线调度
-
求解思路
-
先分析出最优子结构性质是什么


-
然后说根据这个可以构造出状态转移方程

-
-
为什么能DP
-
证明最优子结构性质
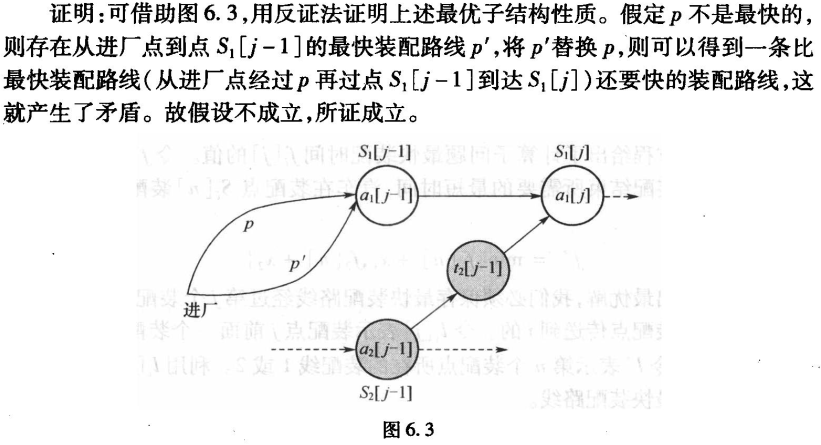
-
递归方程


-
说明重叠子问题

-
-
伪代码

-
时间复杂度分析

矩阵链乘法
-
问题描述

-
最优子结构性质

-
状态转移方程(区间DP)
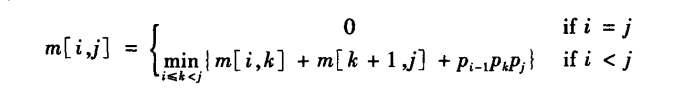
-
填表
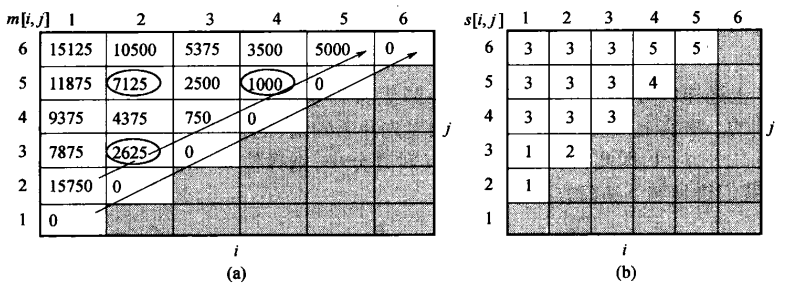
\(i>j\),即对角线以下不填\(i = j\),副对角线填0
之后沿着平行对角线方向从下往上填
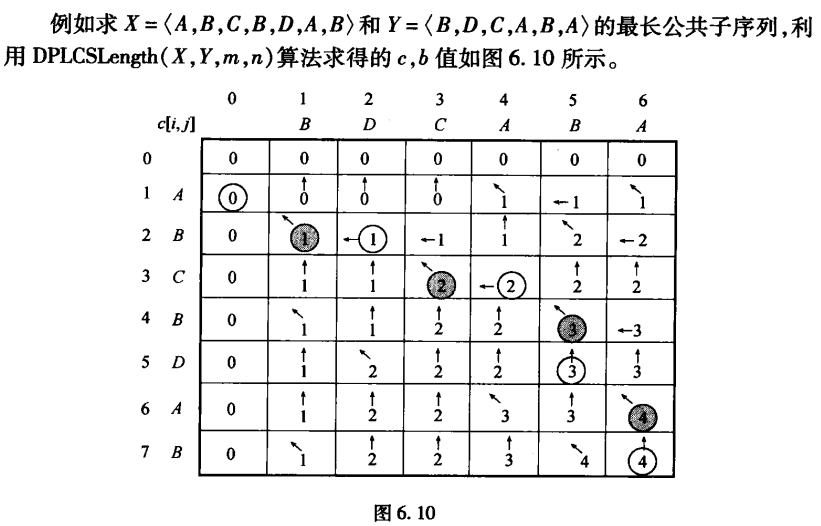
最长公共子序列
-
问题描述

-
最优子结构性质

-
状态转移方程
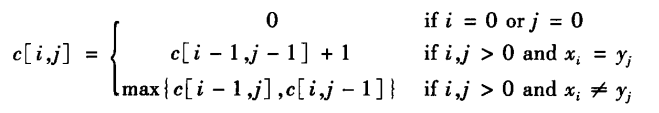
-
填表

例子:
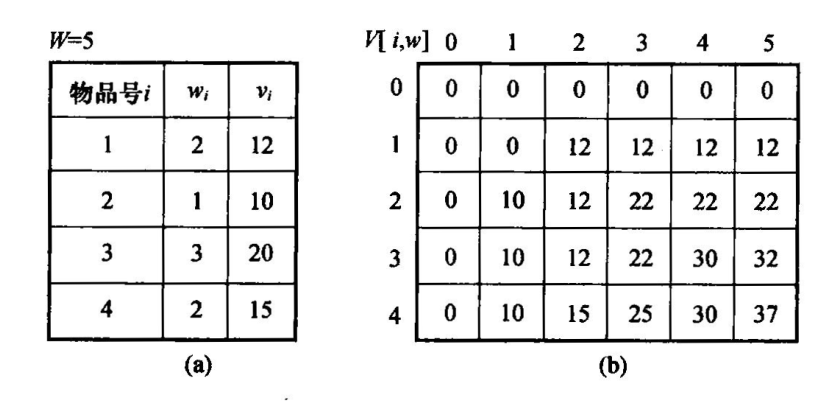
0/1背包
-
问题描述

-
最优子结构性质

-
状态转移方程
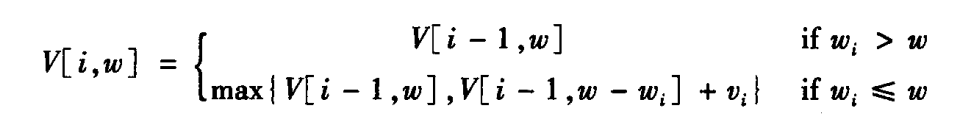
-
填表
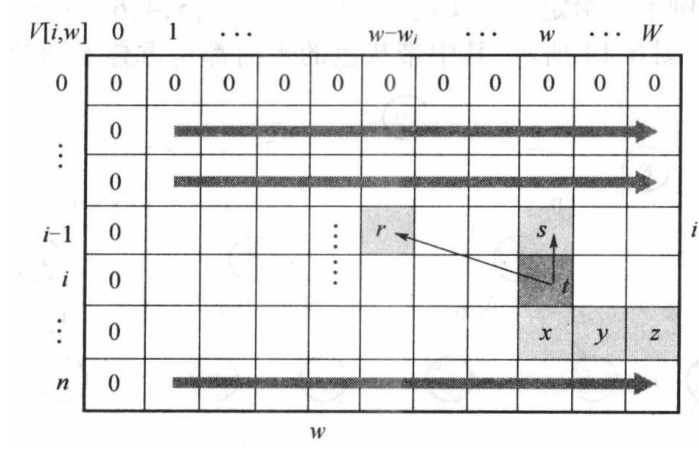
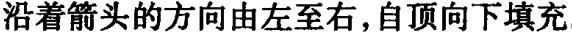
例子
做题
-
求解思路
- 最优子结构性质是什么
- 原问题的一个最优解要用到哪些子问题
- 包含在原问题里的这些子问题的解是它们的最优解
- 由最优子结构性质,描述状态转移方程的构造思路
- 最优子结构性质是什么
-
为什么能DP
-
证明最优子结构性质
-
定义:原问题的最优解中所包含的子问题的解是子问题的最优解
-
证明方法
反证法
已知当前解是原问题的最优解。假定当前解中的\(p\)不是子问题的最优解,则子问题存在最优解\(p^{'}\),将\(p^{'}\)替换\(p\),则可以得到原问题的更优解,矛盾。故假设不成立,则\(p\)就是子问题的最优解。
-
-
说明重叠子问题
- 定义:重复出现的子问题
- 从递归方程可知,划分后的子问题都需要求解相同的“子子问题”
-
写状态转移方程
-
-
伪代码
-
时间复杂度分析
回溯
代码实现:深搜
解空间
子集树
-
定义:求\(n\)个元素的子集
-
伪代码模板
-
递归写法

-
迭代写法

-
排列树
-
定义:求\(n\)个元素的排列
-
伪代码模板

装载问题
-
问题描述

-
约束函数
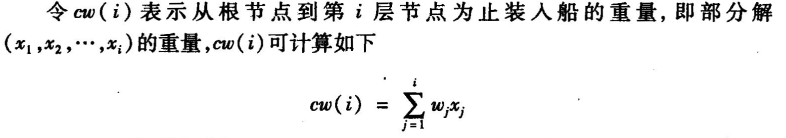
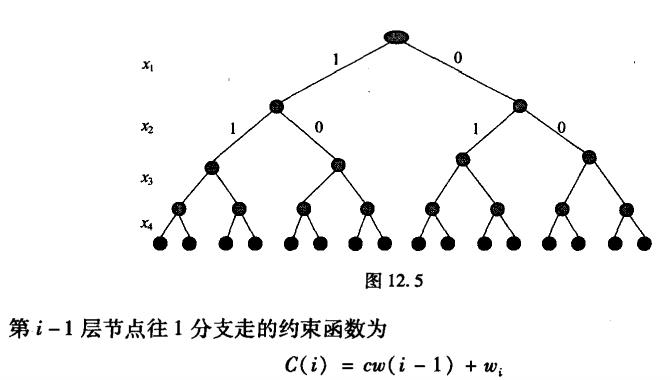
-
限界函数(上界)

-
伪代码

0/1背包问题
-
约束函数

-
限界函数


-
伪代码
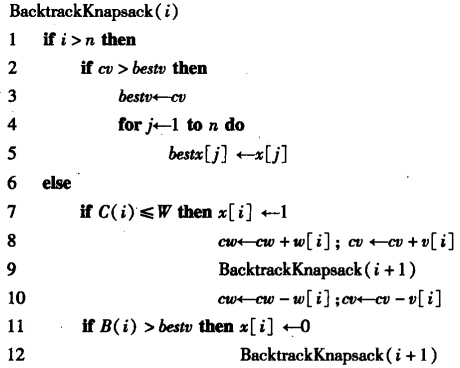
着色问题
-
问题描述

-
伪代码

-
时间复杂度

n皇后问题
-
问题描述

-
约束函数

-
伪代码

旅行商(TSP)问题
-
问题描述

-
限界函数

-
伪代码(排列数)

流水作业调度
-
问题描述

-
限界函数

-
伪代码

分支限界
代码示例
- 不保存解
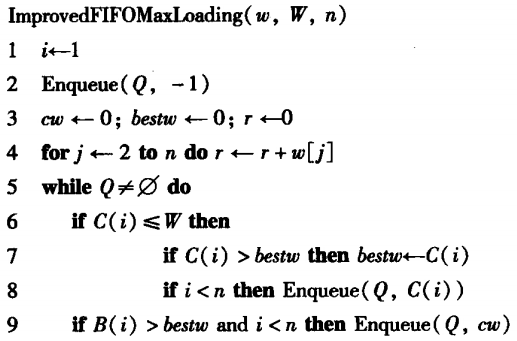
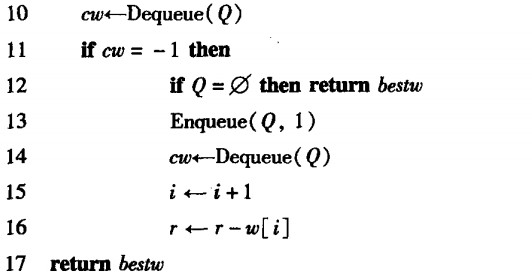
-
保存解
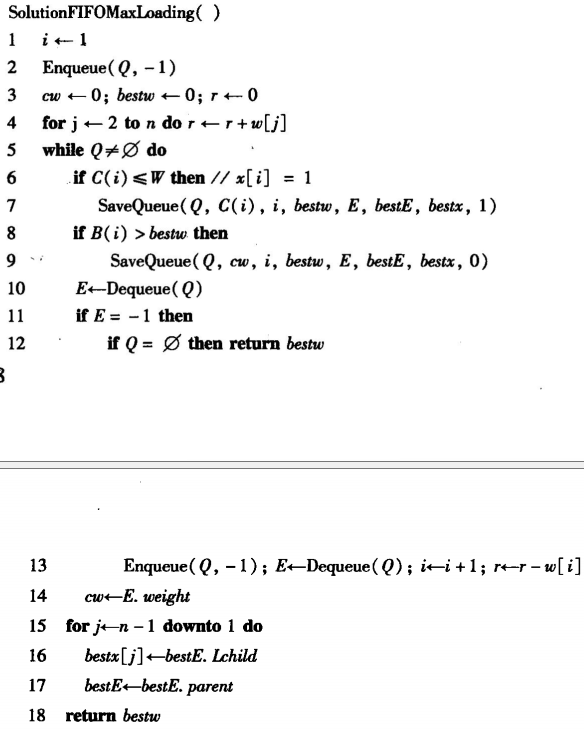
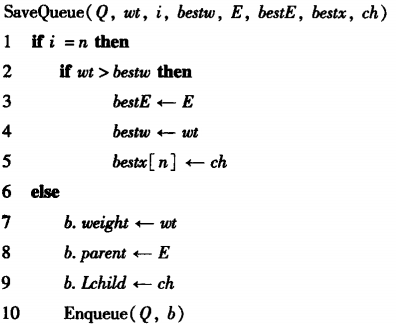
NP完全理论
判定问题和优化问题
抓住优化问题追求的指标,给这个指标加一个阈值就可以转化为判定问题了
求最大值是\(>=\),求最小值是\(<=\)
- TSP
- 优化问题:给定一个完全无向带权图\(G\),要找到\(G\)中回路总权值最小的汉密尔顿回路
- 判定问题:给定一个完全无向带权图\(G\),是否能找到一条回路总权值\(<=k\)的汉密尔顿回路?
- 0/1背包问题
- 优化问题:给定一个物品集合,每个物品有重量和价值。背包有一个最大载重量。要求在不超过最大载重量的条件下装入背包的最大价值。
- 判定问题:给定一个物品集合,每个物品有重量和价值。背包有一个最大载重量。是否能在不超过最大载重量的条件下使得装入背包的价值至少为\(k\)
已知判定问题的算法,怎么利用它求出解
-
二分
-
遍历
设定变量\(j\),初始化为0。将\(j\)传入判定问题的算法中,若返回结果为真,则将\(j\)加1。直到\(j=k\)是判定结果为真,\(j=k+1\)时判定结果为假,则0/1背包问题的解为\(k\)。
证明NPC
-
证明是NP问题
(要证优化问题是NP问题,等价于证明判定问题是NP问题,只需描述对于给定的一个解,怎么在多项式时间内输出是或否即可)(不确定算法,这个解判定为“是”,那整个判定问题就是“是”)
首先,证明0/1背包问题\(\in\)NP。因为对于给定选择的m件物品的重量、价值和背包容量,要验证判定问题只需将这些物品的重量和价值分别相加并与最大载重量和\(k\)比较,显然可在多项式时间内完成。
-
再证明一个已知的 NPC 问题能在多项式时间内归约到它。
要将\(A\)规约到\(B\),就是找到一种方法,将A的问题转化为B的问题,且转化后同解。
-
要求:转化方法是多项式时间的
-
技巧:证明一个优化问题是NPC等价于证明它的判定问题是NPC,所以我们有四种组合,可以选一种有思路的。
-
如何转化

旅行商问题(Traveling Salesman Problem,简称TSP)是一个经典的组合优化问题。在TSP中,给定一系列城市和它们之间的距离,问题要求找到一条最短路径,使得从起始城市出发,经过每个城市恰好一次,并回到起始城市。证明TSP是NP完全的可以分为两个步骤:证明TSP属于NP问题集合,以及证明TSP是NP难问题。首先,我们来证明TSP属于NP问题集合。为了证明一个问题属于NP类,需要证明如果给定一个解,可以在多项式时间内验证该解的正确性。对于TSP,假设有一个解(即一条路径),我们可以通过以下方式验证它是否正确: 验证路径是否访问了每个城市一次。 验证路径的总长度是否小于等于给定的长度限制。 以上两个验证步骤可以在多项式时间内完成,因此TSP属于NP问题集合。其次,我们需要证明TSP是NP难问题。为了证明一个问题是NP难问题,可以使用约减(reduction)的方法,即将已知的NP难问题约化为待证明问题。我们选择一个已知的NP难问题,如图论中的汉密尔顿回路问题(Hamiltonian Cycle Problem),来与TSP进行约减。汉密尔顿回路问题是指在一个无向图中找到一条通过每个顶点恰好一次的闭合路径。我们可以将汉密尔顿回路问题约化为TSP的实例。给定一个图G和一个整数k作为汉密尔顿回路问题的实例,我们构造一个TSP的实例,其中城市对应于图G的顶点,距离由图G的边权重来表示,并将长度限制设置为k。现在,如果图G存在一个汉密尔顿回路,那么等价的TSP实例也存在一条路径,该路径经过每个城市一次且总长度小于等于k。反之亦然。因此,我们成功地将已知的NP难问题(汉密尔顿回路问题)约化为TSP的实例,说明TSP是NP难问题。综上所述,我们证明了旅行商问题(TSP)是NP完全的,即属于NP问题集合并且是NP难问题。
-
定义
P问题就是在多项式时间内可以解决的问题。
NP问题就是在多项式时间内可以验证给出的一个解的问题
NPC 问题:① 首先,它得是一个 NP 问题;② 然后,所有的 NP 问题都可以在多项式时间内归约到它。
NPC归约关系
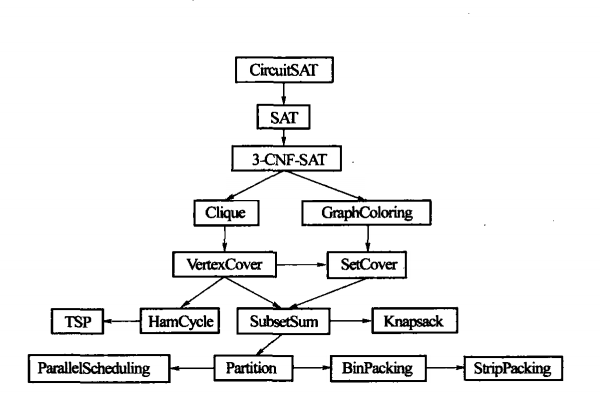
最大流
最大流最小割


FF方法

SPA
\(O(|V||E|^2)\)

Dinic
\(O(|V|^2|E|)\)

图论
伪代码表示
- 除了源点外的所有点:for each vertex \(u \in V - {s}\) do
- 入队:Enqueue(Q, s)
- 出队:Dequeue(Q, s)
- u的所有邻点:for each \(v \in Adj[u]\) do


 浙公网安备 33010602011771号
浙公网安备 33010602011771号