常用代码模板6——贪心

贪心

6. 夹逼定理（若a >= b, b >= a，则a == b）

证明用当前方法得到的结果就等于最优解

区间问题

可以尝试的突破口：排序（按左端点或右端点或双关键字排序）

常用证明方法:

1. 基本思路：夹逼定理（ans >= cnt，ans <= cnt）
2. 反证法
3. 最优解中的区间一定可以换成用贪心策略选出的区间

huffman树

树的带权路径长度

设二叉树具有n个带权叶结点，从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度（Weighted Path Length of Tree，WPL）。

设\(w_i\)为二叉树第i个叶结点的权值，\(l_i\)为从根结点到第i个叶结点的路径长度，则 WPL 计算公式如下：

\[WPL=\sum_{i=1}^{n}w_il_i \]

结构

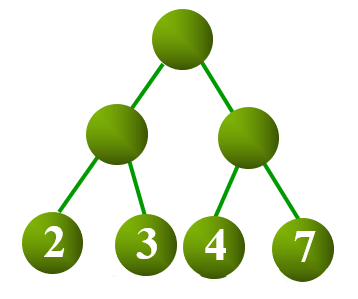
对于给定一组具有确定权值的叶结点，可以构造出不同的二叉树，其中，WPL 最小的二叉树 称为 霍夫曼树（Huffman Tree）。

对于霍夫曼树来说，其叶结点权值越小，离根越远，叶结点权值越大，离根越近。

霍夫曼算法

霍夫曼算法用于构造一棵霍夫曼树，算法步骤如下：

1. 初始化：由给定的n个权值构造n棵只有一个根节点的二叉树，得到一个二叉树集合 。
2. 选取与合并：从二叉树集合F中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
3. 删除与加入：从F中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到F中。
4. 重复 2、3 步，当集合中只剩下一棵二叉树时，这棵二叉树就是霍夫曼树。

对于未建好的霍夫曼树，直接求其 WPL

priority_queue<int, vector<int>, greater<int>> q;
for (int i = 0; i < n; i ++ ) q.push(w[i]);
int ans = 0;
while (q.size() > 1)
{
    int a = q.top(); q.pop();
    int b = q.top(); q.pop();
    ans += a + b;
    q.push(a + b);
}
cout << ans;

证明：WPL最小

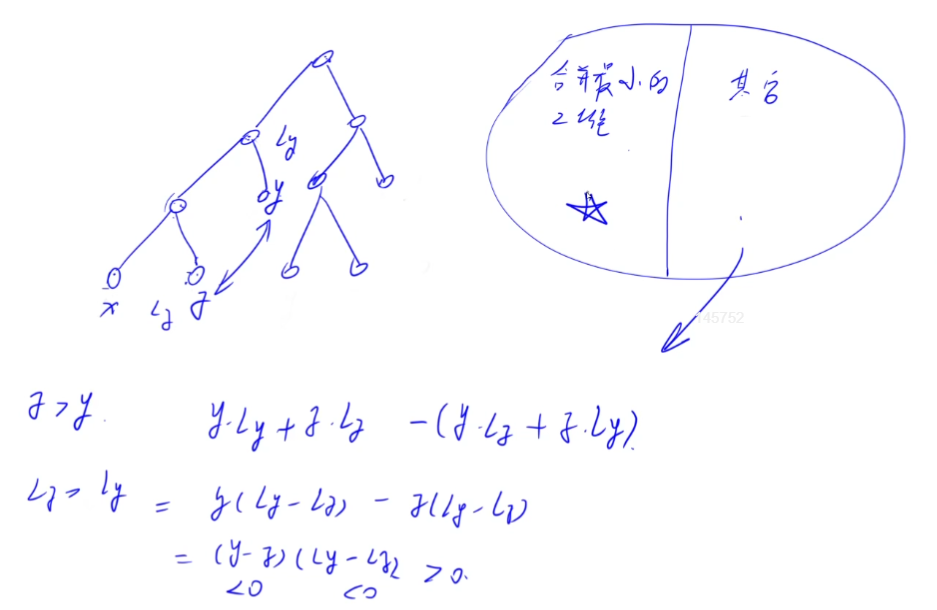
1. 最小的两堆深度最深且可以互为兄弟。
   1. 如果x, y在同一层，将它们的位置变成兄弟不改变结果
   2. 如果y在更高层，有图中算式得交换成兄弟位置一定更好
2. 接下来的递归解决即可

排序不等式

证明方法：微扰+作差

绝对值不等式

求x，使得|a - x| + |b - x|最小，则令x在[a, b]中，a < b