常用代码模板5——动态规划
动态规划模型
dp分析法
- 状态表示
- 集合描述:所有满足条件1、条件2、……的元素的集合(其中每个条件对应状态表示的每一维、元素意义对应求解的量)
- 集合属性:最大值,最小值,数量
- 目标:在集合定义下,答案是什么
- 状态计算(集合的划分:将当前要求的状态进行划分为若干个真子集(抓住定义),原则是不漏、求数量要求不重复,由前面得到的状态值,算出当前状态值)
- 状态转移方程
- 边界(最初子问题的解)(从状态表示出发)
技巧:
- 如果状态转移方程中有i - 1,那数组下标一般从1开始,否则一般从0开始
- 时间复杂度:状态数量 * 转移一次的计算量
- 划分方式:
- 以最后一步的所有选择划分
背包问题
01背包
模型:
有N件物品和一个容量为V的背包。第i件物品的体积是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大。
特点:每件物品仅有一件,可以选择放或不放。

// 边界:f[0][0~v] = 0
// c[]存物体的体积, w[]存物体的价值
// 二维数组
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= v; j ++ )
{
f[i][j] = f[i - 1][j];
if (j >= c[i])
f[i][j] = max(f[i][j], f[i - 1][j - c[i]] + w[i]);
}
cout << f[n][v]; // 答案
// 一维数组
// 第i轮循环求的是从前i个物品中挑,总体积不大于0~v的选法的最大价值,结果存在f[]中。所以在第i轮循环开始时,f[]中存的是从前i-1个物品中挑选,总体积不大于0~v的选法的最大价值。由于总体积在0~c[i]-1的选法的最大价值不变,所以只需要更新总体积c[i]~v的选法的最大价值即可。又因为这一轮f[j]的更新要用到上一轮f[j - c[i]]的值,所以j要从最大值v开始递减到c[i], 保证在更新f[j]时f[j - v[i]]还是上一轮的结果。
for (int i = 1; i <= n; i ++ )
for (int j = v; j >= c[i]; j -- )
f[j] = max(f[j], f[j - c[i]] + w[i]);
cout << f[v];
完全背包
模型:
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的体积是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大。
特点:每件物品有无限个
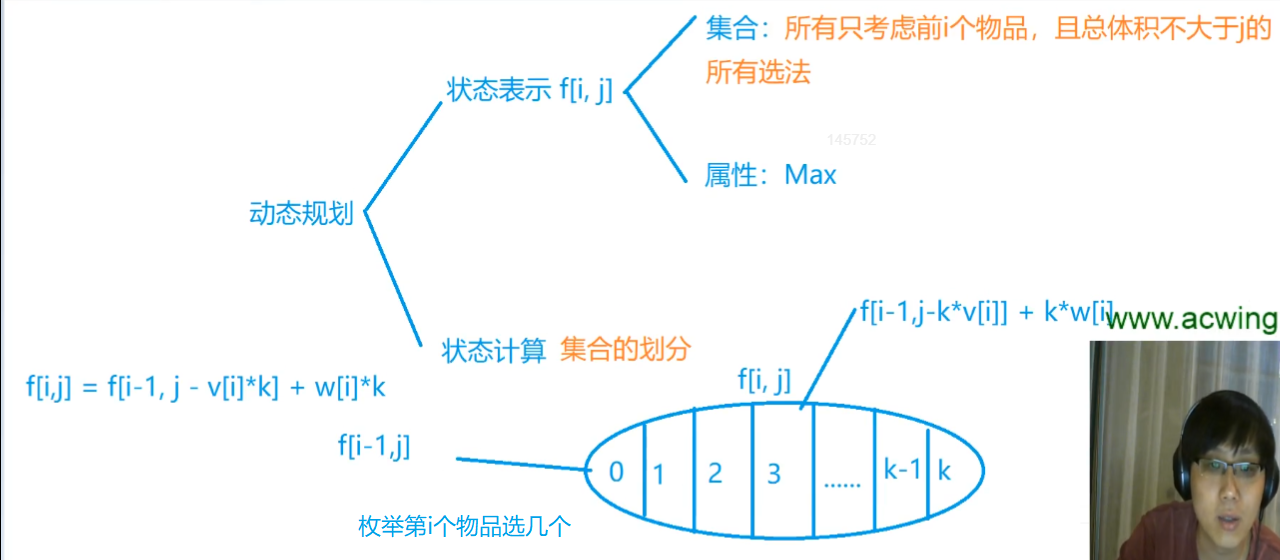

完全背包状态转移方程的另一种理解:
分类:
- 不选i,那就是在前i - 1个中选,总体积不超过j。
f[i - 1][j] - 选了i,那就一定选了一个i,总体积剩下j - v[i],由于i有无限个,可以继续选,所以相当于选了一个i后再在前i个中选,总体积不超过j - v[i]。
f[i][j - v[i]] + w
以上两种划分不重不漏:f[i][j] = f[i - 1][j] + f[i][j - v[i]] + w
// 朴素做法
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
// 二维数组
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j];
if (j >= v[i])
f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m];
// 一维数组
// 与01背包不同的是,对于总体积不大于v[i]~m的选法的最大值是用这一轮的f[j - v[i]]更新的,所以要从小到大循环,先算出小的。
for (int i = 1; i <= n; i ++ )
for (int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
多重背包
模型:
有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件体积是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大。
特点:每件物品有限个,第i种物品有n[i]个
朴素做法类似于完全背包,枚举第i个物品选0~s[i]个,状态转移方程:
f[i][j] = max(f[i - 1][j - k * v[i]] + k * w[i]), k = 0, 1,.., s[i]
// 朴素做法
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
cout << f[n][m];
二进制优化:将每个s[i] 分解成1, 2, 4, 8, ..., 2 ^ k, c,其中2 ^ (k + 1) < s[i], c = s[i] - (2^(k + 1) - 1),保证1~s[i]中的任何一个数可以由这些数组合出来,且这些数的总和刚好是s[i]。这样的话,我们就可以把s[i]件物品分别打包成1件, 2件, ..., c件,每一包就看成一个体积为k * v[i], 价值为k * w[i]的物品包,每个物品包只能选一次,转化成了01背包问题。将所有的物品包用01背包的方法来选,得到的结果与朴素做法相同。
int w[N], v[N], f[M];
int cnt, n, m;
while (n -- )
{
int a, b, s;
scanf("%d%d%d", &a, &b, &s);
int k = 1;
while (k <= s)
{
cnt ++ ;
v[cnt] = k * a;
w[cnt] = k * b;
s -= k;
k *= 2;
}
if (s) cnt ++ , v[cnt] = s * a, w[cnt] = s * b;
}
for (int i = 1; i <= cnt; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
分组背包
模型:
有N件物品和一个容量为V的背包。第i件物品的体积是v[i],价值是w[i]。这些物品被划分为若干组,每组中的物品互相冲突,最多选一件。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大。
特点:物品分组,每一组里最多选一件
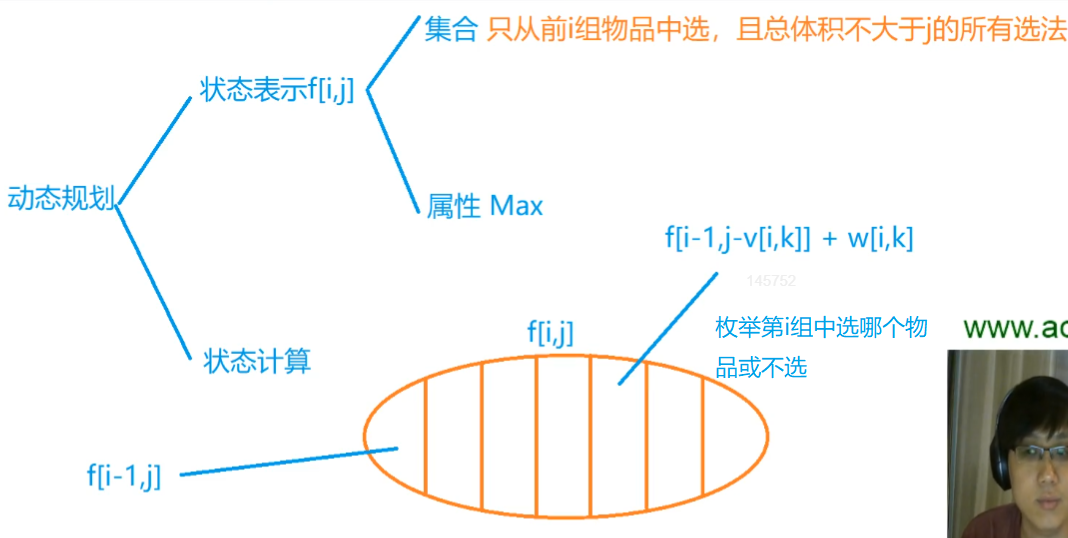
// 二维
int n, m, v[N][N], w[N][N], s[N];
int f[N][N];
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j];
for (int k = 1; k <= s[i]; k ++ )
if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
cout << f[n][m];
// 一维
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 0; j -- )
for (int k = 1; k <= s[i]; k ++ )
if (v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m];
线性DP
DP算法体现为“作用在线性空间上的递推”,从一个或多个边界点开始有方向地向整个状态空间转移、拓展,最后每个状态上都保留了以自身为目标的子问题的最优解。
例如:背包问题中状态空间是一个二维矩阵,状态的值是1行1行算出来的。
数字三角形
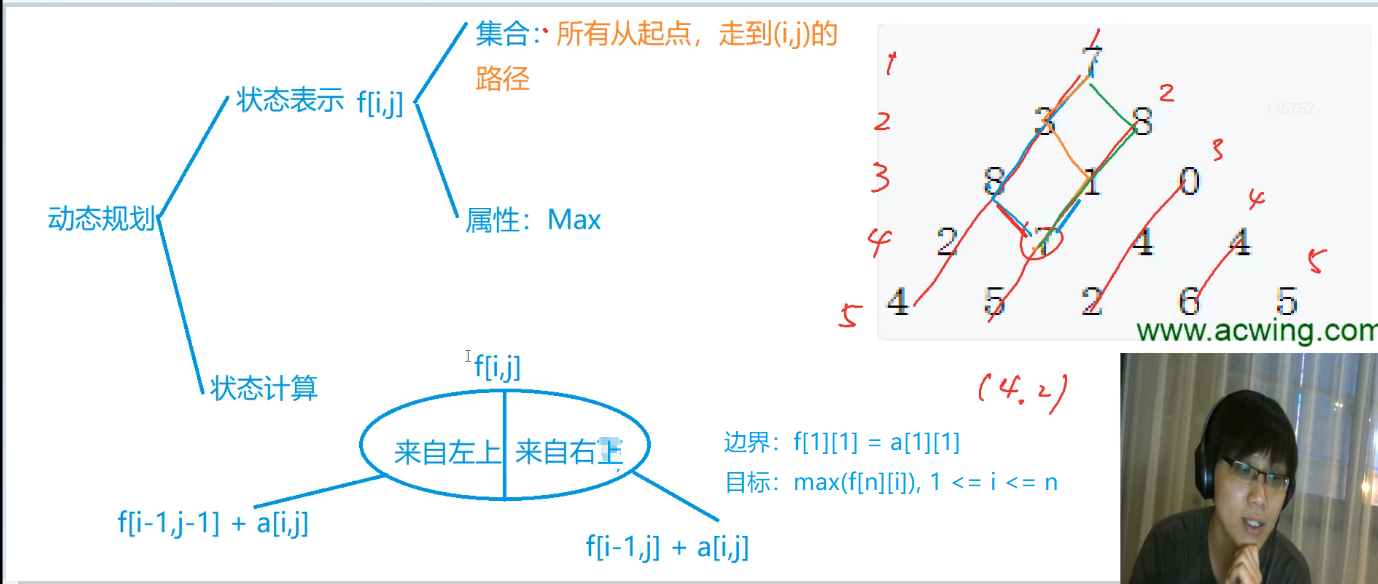
初始化int为负无穷的方法:
0xcf :-8e8 (推荐)
0x8f:-1.8e9
0x9f:-1.6e9
// 自顶向下
memset(f, 0xcf, sizeof f); // 初始化int为负无穷,每个是-8e8
f[1][1] = a[1][1]; // 边界
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
int ans = -inf; // 目标
for (int i = 1; i <= n; i ++ ) ans = max(ans, f[n][i]);
cout << ans;
// 自下而上,从正下方和右下方
for (int i = n; i >= 1; i -- )
for (int j = i; j >= 1; j -- )
f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + f[i][j];
cout << f[1][1] << endl;
最长上升子序列(LIS)
题目:给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
分析:
- 朴素版本:\(O(n^2)\)
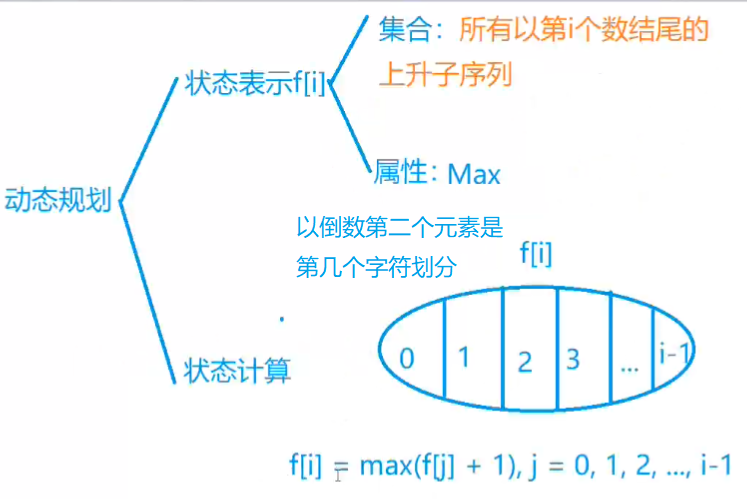
边界:f[i]初始值为1
目标:max{f[i]}, 1 <= i <= n
for (int i = 1; i <= n; i ++ )
{
f[i] = 1;
for (int j = 1; j <= i - 1; j ++ )
if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
}
int ans = 0;
for (int i = 1; i <= n; i ++ ) ans = max(ans, f[i]);
cout << ans;
法二:二分优化:\(O(nlogn)\)
lower_bound(a, a + n, c),返回第一个大于等于c的数的地址。注意,数组存储范围是0~n-1,上界a+n是最后一位下一个的地址。如果c比数组中所有数都小,返回a, 如果c比数组中所有数都大,返回a+n
思路:q[]中记录长度是i的子序列的最小结尾,对于a[i],在q[]找到最大的比a[i]小的数,a[i]的子序列最大长度就是那个数的子序列的长度+1。
关键:
- q[]数组一定升序。因为假设i = j + 1且长度为i的子序列的结尾小于长度为j的结尾,那么以长度为i的倒数第二个字符结尾的子序列长度为j且结尾一定比原长度为j的子序列的结尾要小,与原结尾是最小结尾矛盾。
- 长度相同的子序列,更小的结尾更好。更小的结尾更有可能被后面的a[i]接上。如结尾分别是7、5的长度相同的子序列。如果a[i]=6,那它可以接到5后面,a[i]的长度就可以更长。
// lower_bound也是找到第一个大于等于a[i]的数,如果没有小于它的数,l = 1,直接修改1即可,
// 如果没有大于它的数,会l = len + 1(不存在返回end()),那len = max(len, l)会让len + 1,
// 符合预期效果
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], q[N], len;
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ )
{
int l = lower_bound(q + 1, q + len + 1, a[i]) - q;
len = max(len, l);
q[l] = a[i];
}
cout << len;
return 0;
}
求最长上升子序列的方案数(长度最长的最长上升子序列的数量)例题
设cnt[i]为以a[i]结尾的最长上升子序列的方案数
边界条件,方案数至少是1,因为子序列只有本身也是一种方案
求f[i]时,我们会遍历0~i - 1
- 如果
a[j] >= a[i],跳过 - 如果
a[j] < a[i]- 不求方案数的写法是
f[i] = max(f[i], f[j] + 1) - 求方案数时我们需要判断三种情况
- 情况1:
f[i] == f[j] + 1,说明当前的f[i]还是最优解,它的方案数要加上j的方案数,cnt[i] += cnt[j] - 情况2:
f[i] < f[j] + 1,当前的f[i]不是最优解了,它的方案数应该等于j的方案数,cnt[i] = cnt[j] - 情况3:
f[i] > f[j] + 1,劣于当前最优解,不用管
- 情况1:
- 不求方案数的写法是
最终的方案数就是能取到最大长度的子序列的结尾的cnt[i]之和
代码实现
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 30;
int a[N], f[N], cnt[N];
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int T;
cin >> T;
while (T -- )
{
memset(a, 0, sizeof a), memset(f, 0, sizeof f), memset(cnt, 0, sizeof cnt);
int n;
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> a[i];
for (int i = 0; i < n; i ++ )
{
f[i] = 1, cnt[i] = 1;
for (int j = 0; j < i; j ++ )
{
if (a[j] <= a[i])
{
if (f[j] + 1 == f[i]) cnt[i] += cnt[j];
else if (f[j] + 1 > f[i]) f[i] = f[j] + 1, cnt[i] = cnt[j];
}
}
}
int maxl = *max_element(f, f + n);
int sum = 0;
for (int i = 0; i < n; i ++ )
if (maxl == f[i])
sum += cnt[i];
cout << maxl << ' ' << sum << "\n";
}
return 0;
}
最长公共子序列(LCS)
题目:给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
分析:
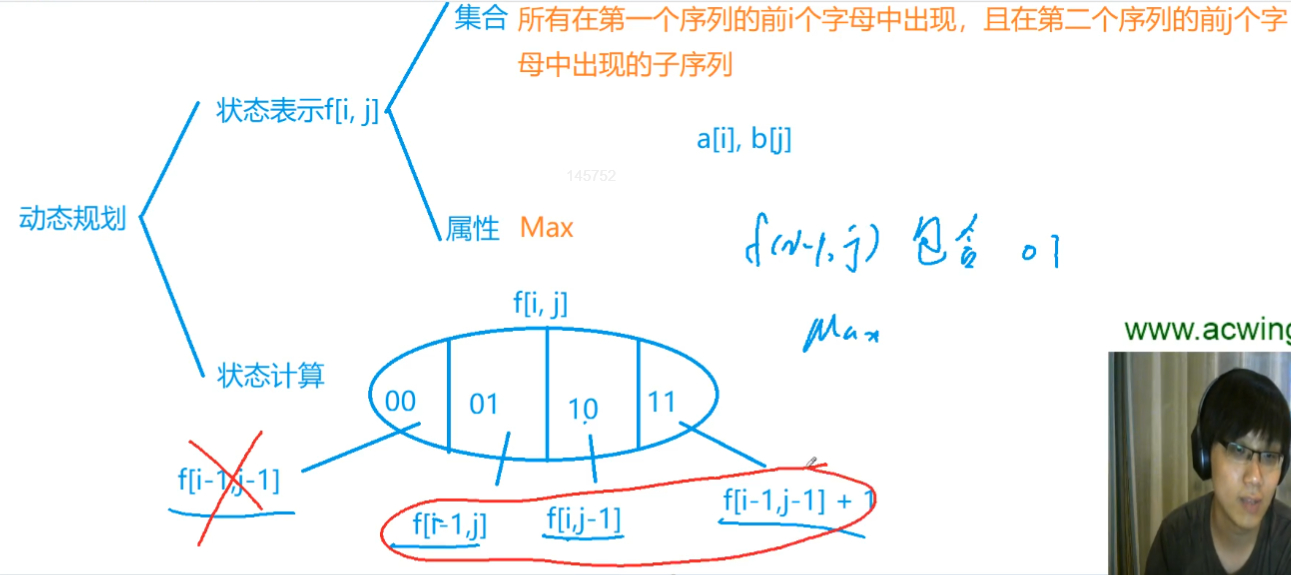
01包含于f[i - 1, j],所以max{01} <= max{f[i -1, j]},同理类推,状态转移方程:
f[i, j] = max{f[i - 1, j], f[i, j - 1], f[i - 1, j - 1] + 1}
目标:f[N, M] ;边界:f[0, 0] = 0
// 下标从1开始
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
cout << f[n][m];
经验:涉及到两个字符串的状态表示可以用二维的f[i, j],i控制第一个字符串,j控制第二个字符串。
区间DP
区间DP也属于线性DP中的一种,它以“区间长度”作为DP的“阶段”,使用两个坐标(区间的左、右端点)描述每个维度。在区间DP中,一个状态由若干个比它更小且包含于它的区间所代表的状态转移而来。区间DP的初态一般就由长度为1的“元区间”构成。
常用模板
所有的区间dp问题枚举时,第一维通常是枚举区间长度,并且一般 len = 1 时用来初始化,枚举从 len = 2 开始;第二维枚举起点 i (右端点 j 自动获得,j = i + len - 1)
for (int len = 1; len <= n; len++) { // 区间长度
for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
int j = i + len - 1; // 区间终点
if (len == 1) {
dp[i][j] = 初始值
continue;
}
for (int k = i; k < j; k++) { // 枚举分割点,构造状态转移方程
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
}
}
石子合并
原题链接:282. 石子合并 - AcWing题库
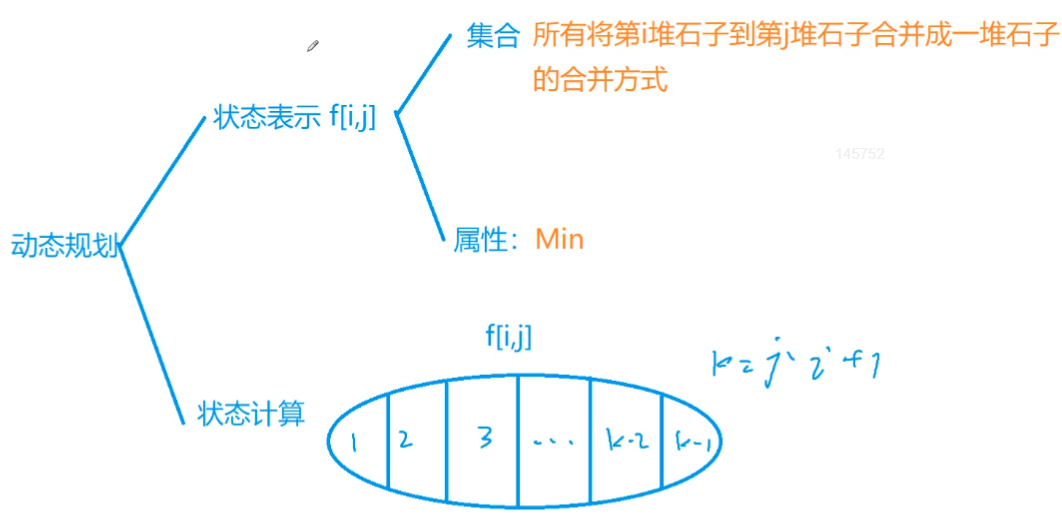
目标:f[1][n]
状态计算:要合并[i, j]内的石堆,选定第k堆石子,先合并[i, k]和[k + 1, j],最后再将这两堆合并,这种方式可以枚举合并[i, j]石堆的所有方法。状态转移方程:
f[i][j] = min(f[i][k] + f[k + 1][j] + s[j] - s[i - 1]), i<= k<= j-1
在区间DP中,一个状态由若干个比它更小且包含于它的区间所代表的状态转移而来。所以区间的状态值应从小到大计算。
边界:f[i][i]= 0
for (int len = 2; len <= n; len ++ ) // len = 1时为0,不用算,区间长度从小到大
for (int i = 1; i + len - 1 <= n; i ++ ) // 枚举长度为len的区间的左端点
{
int l = i, r = len + i - 1; // 每个状态的左右端点
f[l][r] = 0x3f3f3f3f;
for (int k = l; k <= r - 1; k ++ )
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
cout << f[1][n] << endl;
计数类DP
要求集合划分不重不漏,属性是数量
数位统计DP
重点:分情况讨论
状态压缩DP
当前子问题的决策受到前面子问题的影响,但不是像线性DP一样只是简单地由前面的结果得到当前结果,这个影响是一个复杂的集合,我们将这个影响的k种情况,n个维度压缩在一个n位的K进制数里。那么[0, k ^ n - 1]的十进制整数就可以表示所有的影响了。
例如蒙德里安的梦想中:第i - 2列对第i - 1列的影响有两种情况:1. 第i - 2 列的横向小方块伸到了第i - 1列、 2. 第i - 2 列的横向小方块没有伸到了第i - 1列。并且有n行,即n个维度。所以我们把这个状态压缩到一个n位的2进制数中。[0, 2 ^ n - 1]就代表了第i - 2列的所有横向方块的摆法。
拼图
状压DP、矩阵乘法、快速幂
这道题和蒙德里安的梦想很像,是一道状压DP的问题
因为m<=7,因此我们选择用二进制表示一行的状态。一行中,如果某一位为空,用0表示,不空用1表示,则一行的状态可以用0~2^m-1的十进制表示
状态表示:f[i][j]表示第i行的状态为j的方案数
目标:f[n][2^m-1]表示第n行都填满的方案数
状态转移方程:
-
第
i行的状态可以从第i-1行转移过来,求一个转移矩阵w。w[i][j]表示当前行的状态为i,下一行的状态为j的方案数 -
f[i][j]=f[i-1][k] * w[k][j], 0<=k<=2^m-1,第i行的状态为j可以从第i-1行状态为k转移过来。 -
矩阵快速幂加速状态转移
如果不加速,状态数有
n*(2^m-1)个,转移数有2^m-1个,时间复杂度有n*(2^m-1)^2,会超时。我们定义一个向量
F[i]:F[i]=(f[i][0], f[i][1], ..., f[i][2^m-1]), 1*(2^m)可以发现,每次的状态转移就是
F[i]=F[i-1]*w,这个展开即可证明。递推得:
F[i]=F[0]*w^i,则F[n]=F[0]*w^n,其中f[n][2^m-1]=F[n][2^m-1]因此,我们只需根据题意初始化边界
F[0],再用矩阵快速幂在logn的时间内算出w^n,两者相乘即可在logn的时间内算出f[n][2^m-1]了。
边界:f[0][2^m-1]=1, 其余f[0][i]都为0,第一行的图形不能突到第0行去,因此第0行只有全为1这一种状态,方案数为1,其余的状态的方案数必须是0
时间复杂度:
- 转移矩阵用
dfs求,最多有(2^7-1)^2=16129 log1e15<50,不会超时
转移矩阵的dfs实现:
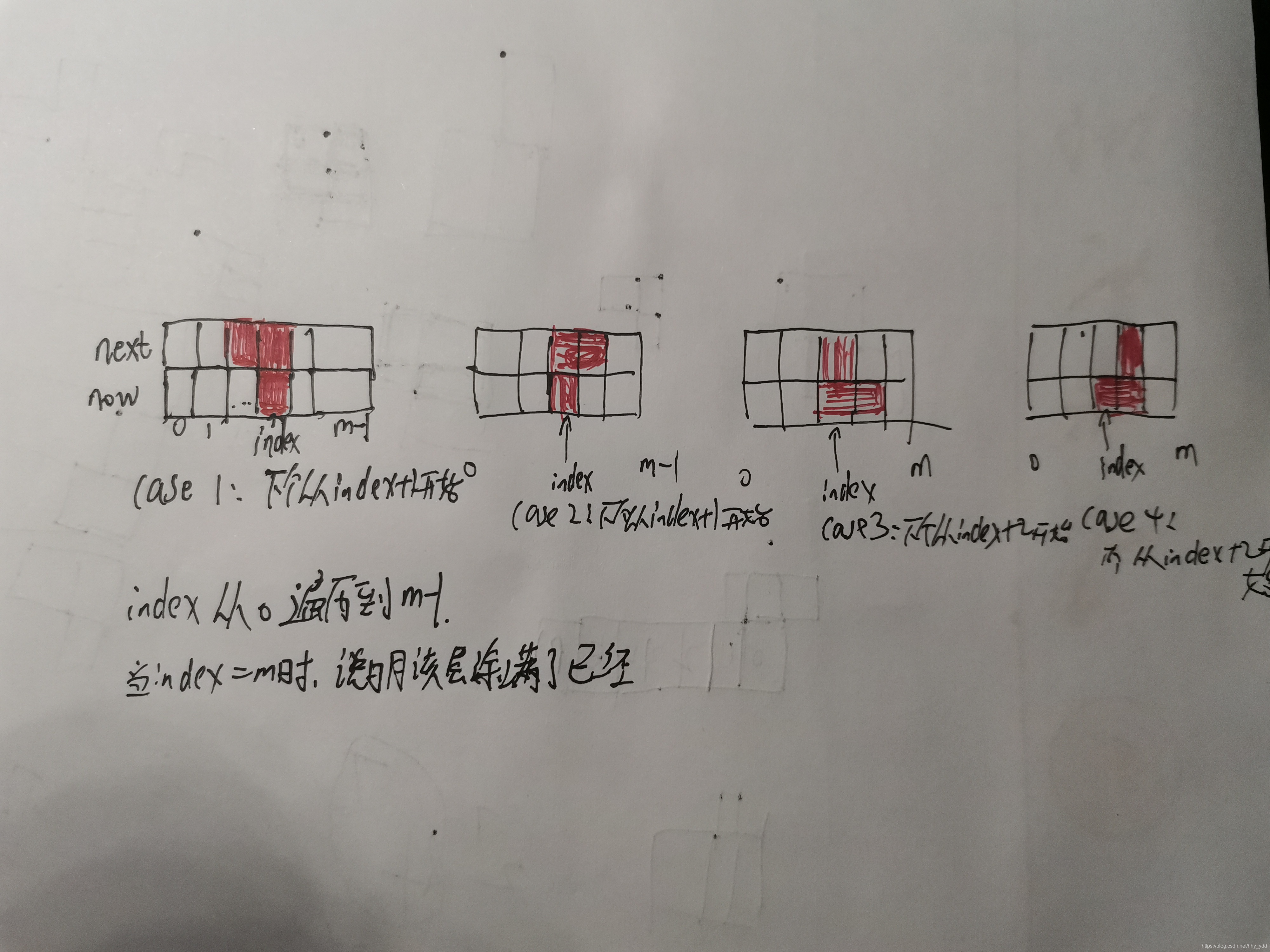
通过dfs,寻找转移矩阵。now是当前行的状态,从0遍历到2^m - 1,next是下一行的状态,index是当前行即now的第index个方格,从0开始,到m-1。当index=m时,说明当前行已经填充满,此时的next的值,代表填充完now可以转移到的状态。
#include <bits/stdc++.h>
using namespace std;
#define dbg(...) fprintf(stderr, __VA_ARGS__)
using ll = long long;
using pii = pair<int, int>;
const int N = 130, mod = 1e9 + 7;
int w[N][N];
int F[N][N]; // 注意虽然F[][]矩阵真正有用的的只有第一行,但是函数不仅要处理f*w, 还要处理w*w,因此要保证f和w是同形的,都是N*N
ll n, m;
void dfs(int now, int next, int index)
{
if (index == m)
{
w[now][next] += 1;
return;
}
else if ((now >> index) & 1) dfs(now, next, index + 1);
else
{
if (index > 0 && !((next >> index) & 1) && !((next >> (index - 1) & 1))) // case1
dfs(now, next + (1 << index) + (1 << (index - 1)), index + 1);
if (index < m - 1 && !((next >> index) & 1) && !((next >> (index + 1)) & 1)) // case 2
dfs(now, next + (1 << index) + (1 << (index + 1)), index + 1);
if (index < m - 1 && !((now >> (index + 1)) & 1))
{
if (!((next >> index) & 1)) // case3
dfs(now, next + (1 << index), index + 2);
if (!((next >> (index + 1)) & 1)) // case4
dfs(now, next + (1 << (index + 1)), index + 2);
}
}
}
// 矩阵乘法,注意虽然F[][]矩阵真正用到的只有第一行,但是这个函数不仅要处理f*w, 还要处理w*w,因此要保证f和w是同形的,都是N*N
void mul(int c[][N], int a[][N], int b[][N])
{
static int tmp[N][N]; // 防止每次都开一个新的
memset(tmp, 0, sizeof tmp);
for (int i = 0; i < (1 << m); i ++ )
for (int j = 0; j < (1 << m); j ++ )
for (int k = 0; k < (1 << m); k ++ )
tmp[i][j] = (tmp[i][j] + (ll)a[i][k] * b[k][j]) % mod;
memcpy(c, tmp, sizeof tmp);
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m;
// 求转移矩阵
for (int i = 0; i < (1 << m); i ++ )
dfs(i, 0, 0);
F[0][(1 << m) - 1] = 1; // 初始化边界
while (n) // 矩阵快速幂求F[0]*w^n,即F[0] * w^n = F[0] * w^(2^i) * w^(2^j) * ...
{
if (n & 1) mul(F, F, w);
mul(w, w, w);
n >>= 1;
}
cout << F[0][(1 << m) - 1]; // 此时的F[0][2^m-1]就是f[n][2^m-1]
return 0;
}
树形DP
树的直径
树形 DP 可以在存在负权边的情况下求解出树的直径。
const int N = 10000 + 10;
int n, d = 0;
int d1[N], d2[N];
vector<int> E[N];
void dfs(int u, int fa) {
d1[u] = d2[u] = 0;
for (int v : E[u]) {
if (v == fa) continue;
dfs(v, u);
int t = d1[v] + 1;
if (t > d1[u])
d2[u] = d1[u], d1[u] = t;
else if (t > d2[u])
d2[u] = t;
}
d = max(d, d1[u] + d2[u]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d %d", &u, &v);
E[u].push_back(v), E[v].push_back(u);
}
dfs(1, 0);
printf("%d\n", d);
return 0;
}
记忆化搜索
可解的前提是状态空间是拓扑图,即不存在环
优点:可以更快地实现状态转移方程。
线性DP可以用循环,区间DP用记忆化搜索更好写。
状态机DP
股票买卖系列
状态机DP
最多交易一次
特点:最多交易一次
解法:既然只能交易一次,一共1~n天,如果在第i天买了股票,要获得最大利润,肯定要在i+1~n天中股票价格最高的那天出售。
算法实现:维护一个后缀数组suffix,suffix[i]存的是i~n的股票价格最大值。然后从第一天开始遍历,第i天购买股票的最大利润是suffix[i+1]-prices[i]。
#define LOCAL
#ifdef LOCAL
#define dbg(...) fprintf(stderr, __VA_ARGS__)
#else
#define dbg(...)
#define NDEBUG
#endif
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 10;
int w[N];
int suffix[N];
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
for (int i = n; i >= 1; i -- ) suffix[i] = max(suffix[i + 1], w[i]);
int ans = 0;
for (int i = 1; i < n; i ++ ) ans = max(ans, suffix[i + 1] - w[i]);
cout << ans;
return 0;
}
不限交易次数
分析:相比于上一题,从最多交易一次变成可以无限次交易了,用状态机DP来解
解法
-
状态表示
f[i][0]:第i天结束,手中没有股票的情况下的最大利润f[i][1]:第i天结束,手中有股票的情况下的最大利润 -
状态转移方程
要点:第
i-1天的结束就是第i天的开始
分析:
-
第
i天结束时手中没有股票,有两种情况。一是前一天手中没有股票且今天没有交易,那利润不变;二是前一天手中有股票今天卖出去了,那利润加上今天的股票价格。所以有:f[i][0] = max(f[i-1][0], f[i-1][1]+price[i]) -
第
i天结束时手中有股票,有两种情况。一是前一天手中有股票且今天没有交易,那利润不变;二是前一天手中没有股票今天买了股票,那利润减去今天的股票价格。所以有:f[i][1] = max(f[i - 1][1], f[i - 1][0] - price[i])
-
-
边界条件
第0天结束,也就是第1天开始时,不可能持有股票,因此不能从
f[0][1]转移过来,要将f[0][1]置为负无穷;第1天开始时不持有股票是合理的,此时利润是0,因此f[0][0]=0 -
答案
第n天结束时,如果手中还有股票,那就是之前买了没卖出去,亏了。因此我们取第n天结束时手中没有股票的情况。答案是
f[n][0]
#define LOCAL
#ifdef LOCAL
#define dbg(...) fprintf(stderr, __VA_ARGS__)
#else
#define dbg(...)
#define NDEBUG
#endif
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 10;
int w[N];
int f[N][2];
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
f[0][1] = -0x3f3f3f3f;
for (int i = 1; i <= n; i ++ )
{
f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
}
cout << f[n][0];
return 0;
}
最多交易K次
分析:与上一题相比,限制了最多交易K次,因此我们要加一维状态来记录交易次数
解法
-
状态表示
f[i][j][0]:第i天结束,交易j次,手中没有股票的情况下的最大利润f[i][j][1]:第i天结束,交易j次,手中有股票的情况下的最大利润注意:买入卖出算一次交易,我们在买入的时候交易次数加1,卖出时交易次数不变
-
状态转移方程
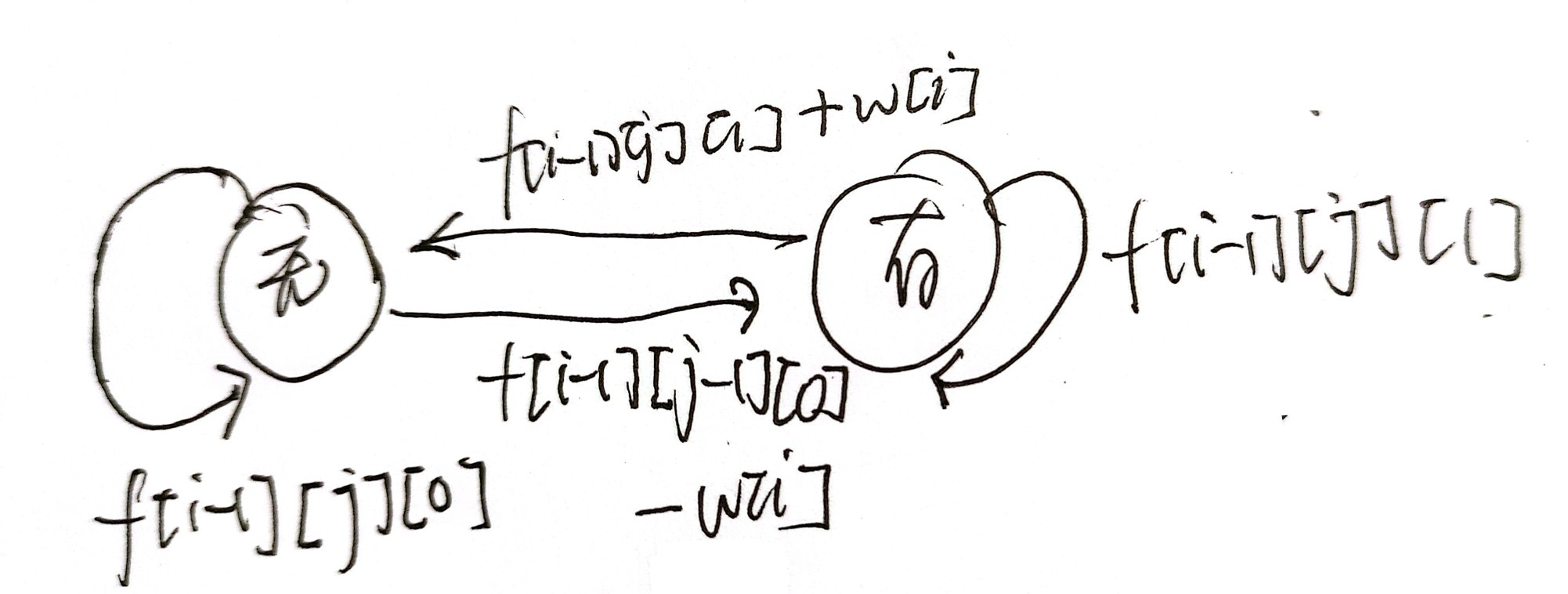
分析:
-
第
i天结束时手中没有股票,交易了j次,有两种情况。一是前一天手中没有股票且今天没有交易,那利润不变,交易次数不变;二是前一天手中有股票今天卖出去了,那利润加上今天的股票价格,交易次数还是不变。所以有:f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + price[i]); -
第
i天结束时手中有股票,交易了j次,有两种情况。一是前一天手中有股票且今天没有交易,那利润不变,交易次数不变;二是前一天手中没有股票今天买了股票,那利润减去今天的股票价格,交易次数加1。所以有:f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
等价变形
-
因为我们在用数组写法时,会枚举交易次数从
0~k次,那j-1会越界。我们做一个等价变形,令j->j+1,因此有:f[i][j+1][0] = max(f[i - 1][j+1][0], f[i - 1][j+1][1] + price[i]);f[i][j+1][1] = max(f[i - 1][j+1][1], f[i - 1][j][0] - price[i]); -
这样写的话,
j在循环变量里还是正常枚举0~k
-
-
边界条件
- 第0天结束,第1天开始时,交易次数只能是0,大于0的不合法。
- 第0天结束,第1天开始时,不能持有股票。
- 任何一天的交易次数都不能是负数
- 第1天开始时,交易0次,不持有股票是合法的,利润为0
注意:我们已经把
j向右偏移了一个,写的时候要注意 -
答案
答案就是第
n天结束时,不持有股票,交易次数在0~k次的最大值
#define LOCAL
#ifdef LOCAL
#define dbg(...) fprintf(stderr, __VA_ARGS__)
#else
#define dbg(...)
#define NDEBUG
#endif
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 10, inf = 0x3f3f3f3f, M = 110;
int w[N];
int f[N][M][2];
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
// 第0天结束,第1天开始时,交易次数只能是0,大于0的不合法
// 第0天结束,第1天开始时,不能持有股票。
for (int j = 0; j <= k+1; j ++ ) f[0][j][0] = -inf, f[0][j][1] = -inf;
// 第1天开始时,交易0次,不持有股票是合法的,利润为0
f[0][1][0] = 0;
// 任何一天的交易次数都不能是负数, j->j+1, 因此j=0是就是负数
for (int i = 0; i <= n; i ++ ) f[i][0][0] = -inf, f[i][0][1] = -inf;
// 简单写法 memset(f, -0x3f, sizeof f); f[0][1][0] = 0;
for (int i = 1; i <= n; i ++ )
{
for (int j = 0; j <= k; j ++ )
{
f[i][j + 1][0] = max(f[i - 1][j + 1][0], f[i - 1][j + 1][1] + w[i]);
f[i][j + 1][1] = max(f[i - 1][j + 1][1], f[i - 1][j][0] - w[i]);
}
}
int res = 0;
for (int j = 0; j <= k; j ++ ) res = max(res, f[n][j + 1][0]);
cout << res;
return 0;
}
有冷冻期
分析:这道题在不限交易次数的情况下规定卖出后的第二天不能买入
状态转移
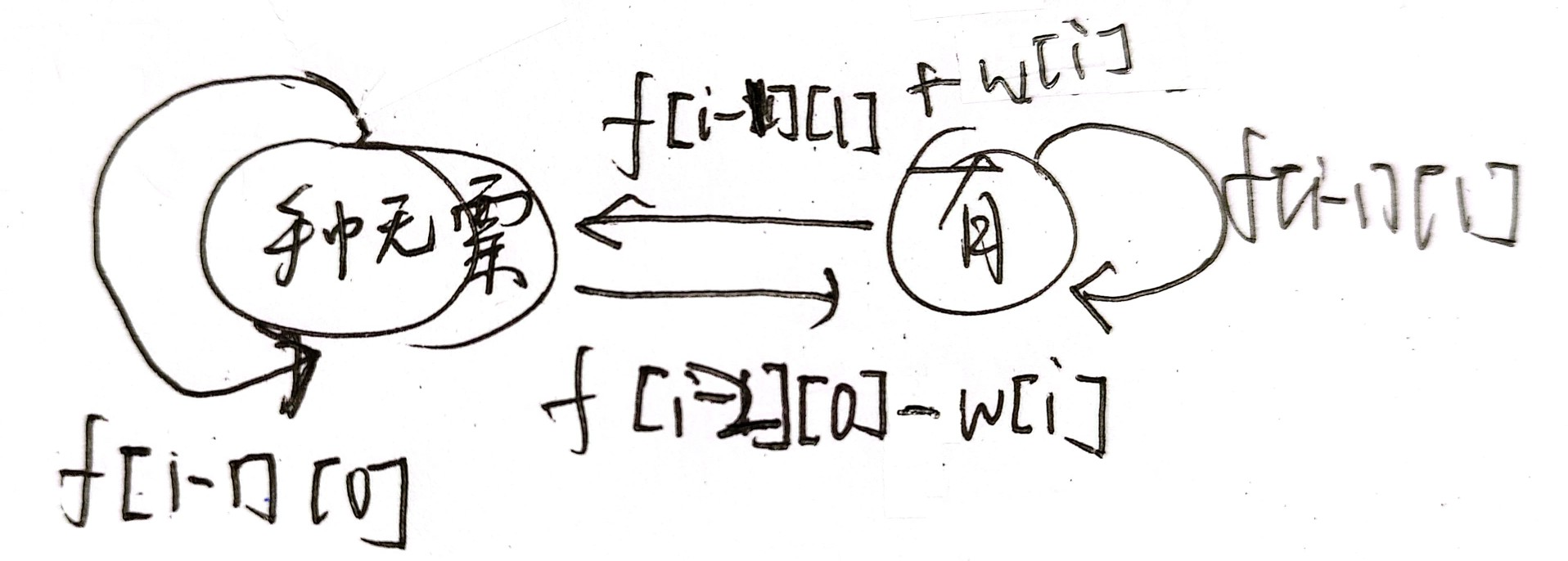
-
加了冷冻期后,要从手中无票的状态转移到手中有票,就必须是前天结束时手中无票,而不能从昨天手中无票转移过来,因为昨天卖了股票后,今天就不能买股票了。如果考虑股票不是昨天卖的,那就是前天结束时手中无票的情况,所以从前天转移是合理的。
-
第
i天结束时手中没有股票,有两种情况。一是前一天手中没有股票且今天没有交易,那利润不变;二是前一天手中有股票今天卖出去了,那利润加上今天的股票价格。所以有:f[i][0] = max(f[i-1][0], f[i-1][1]+price[i]) -
第
i天结束时手中有股票,有两种情况。一是前一天手中有股票且今天没有交易,那利润不变;二是前天结束时手中没有股票今天买了股票,那利润减去今天的股票价格。所以有:f[i][1] = max(f[i - 1][1], f[i - 2][0] - price[i])
等价变形
-
i从1~n枚举,i-2会越界,因为我们将i替换成i+1,则当循环变量i=1时就不会越界了。循环变量i还是从1~n枚举 -
因此有:
注意:当循环变量为
i时,买卖的是第i天的股票,所以price数组下标仍为if[i + 1][0] = max(f[i][0], f[i][1] + price[i]);f[i + 1][1] = max(f[i][1], f[i - 1][0] - price[i]);
边界条件:第0天结束,也就是第1天开始时,不可能持有股票。由于i右移,所以第0天的下标是1,f[1][1] = -inf
答案:第n天手中无票,由于偏移了,第n天的两个状态存在下标n+1的位置,因此答案是f[n+1][0]
#define LOCAL
#ifdef LOCAL
#define dbg(...) fprintf(stderr, __VA_ARGS__)
#else
#define dbg(...)
#define NDEBUG
#endif
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 10;
int w[N], f[N][2];
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
f[1][1] = -0x3f3f3f3f;
for (int i = 1; i <= n; i ++ )
{
f[i + 1][0] = max(f[i][0], f[i][1] + w[i]);
f[i + 1][1] = max(f[i - 1][0] - w[i], f[i][1]);
}
cout << f[n + 1][0];
return 0;
}
有手续费
分析:这道题在不限制交易次数的情况下,规定每次交易都要缴纳手续费c元
解析:其实只需要在状态转移计算利润是多减去一个c即可。由于买卖算一次交易,我们就在买入股票时减去手续费即可,卖出股票时不用减了,因为一次交易只需要缴纳一次手续费。
只需修改第i天手中有票的状态转移为:
f[i][1] = max(f[i - 1][1], f[i - 1][0] - price[i] - c);
原来是
f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
#define LOCAL
#ifdef LOCAL
#define dbg(...) fprintf(stderr, __VA_ARGS__)
#else
#define dbg(...)
#define NDEBUG
#endif
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 10;
int w[N];
int f[N][2];
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n, c;
cin >> n >> c;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
f[0][1] = -0x3f3f3f3f;
for (int i = 1; i <= n; i ++ )
{
f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i] - c);
}
cout << f[n][0];
return 0;
}






 浙公网安备 33010602011771号
浙公网安备 33010602011771号