用向量叉乘求直线交点

求解方法

两个技巧：

• 用向量来表示点，则可以用向量加法来表示点的平移。
• 用点和向量来表示直线，这样可以处理斜率无穷大的情况。

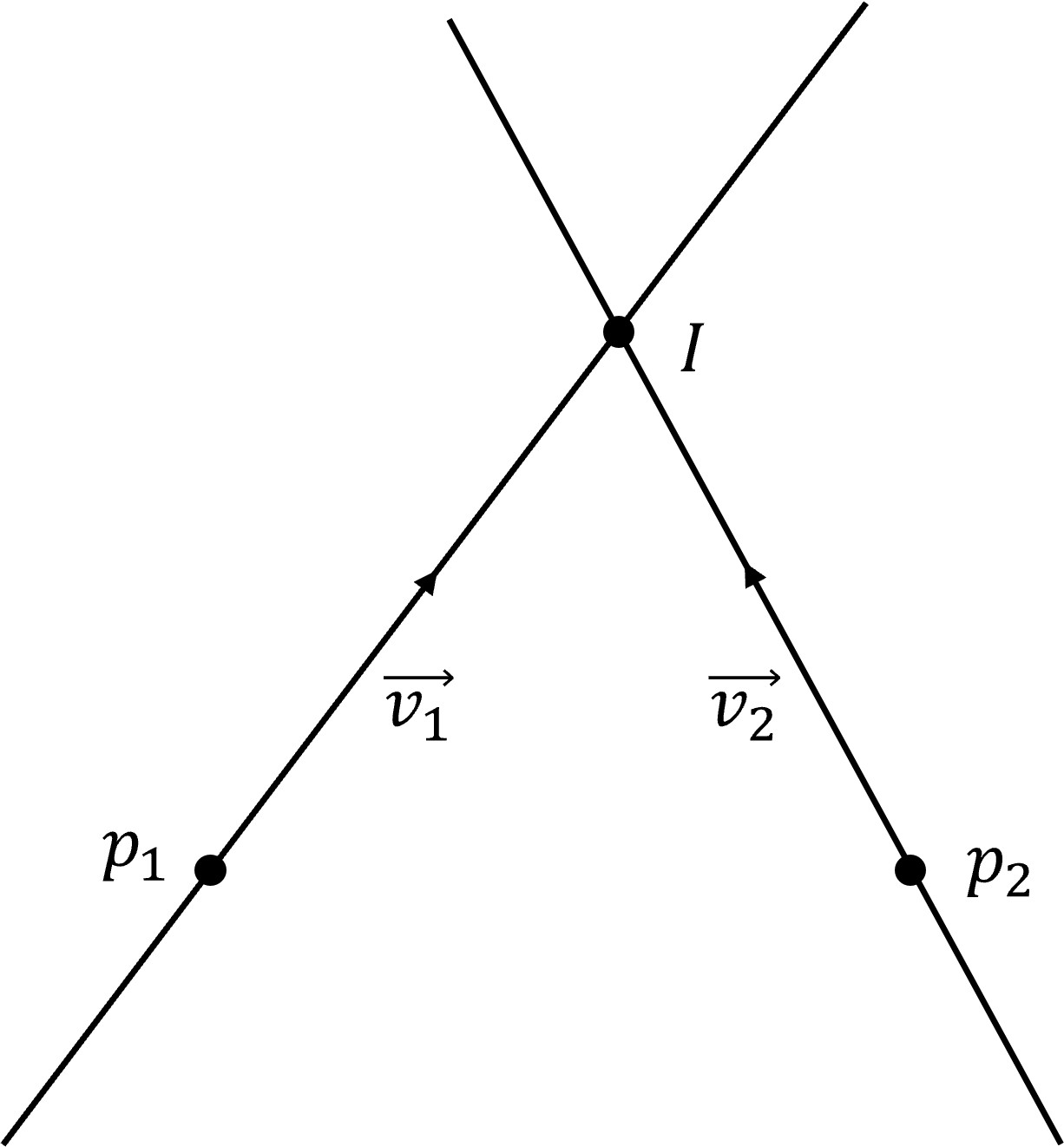
如图所示，有两条直线交于点 \(I\)。我们用点 \(p_1\) 和向量 \(\vec v_1\) 来表示直线 1，用点 \(p_2\) 和向量 \(\vec v_2\) 来表示直线 2。

把点看成向量，则有 \(\mathbf I=\mathbf p_1+t\mathbf v_1\)（用向量加法表示点的平移），现在我们的任务就是求出标量 \(t\)。所谓用向量叉乘来求直线交点，就是利用 \(\overrightarrow{Ip_2}\times\vec v_2=\vec 0\)（两向量平行）这个式子求出 \(t\)。

在开始推导之前，先复习一下向量叉乘的几条运算规律：

• 加法的左分配律：\(\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}\)
• 加法的右分配律：\((\mathbf{a} + \mathbf{b}) \times \mathbf{c} = \mathbf{a} \times \mathbf{c} + \mathbf{b} \times \mathbf{c}\)
• 标量乘法：\((\lambda\mathbf{a})\times\mathbf{b} = \lambda(\mathbf{a}\times\mathbf{b}) = \mathbf{a}\times(\lambda\mathbf{b})\)

下面我们来求解标量 \(t\)，推导过程如下：

\[\begin{array}{rcl} (\mathbf{p}_2 - \mathbf{I}) \times \mathbf{v}_2 &=& \mathbf{0}\\ (\mathbf{p}_2 - (\mathbf{p}_1 + t\mathbf{v}_1)) \times \mathbf{v}_2 &=& \mathbf{0}\\ (\mathbf{p}_2 - \mathbf{p}_1) \times \mathbf{v}_2 - t\mathbf{v}_1 \times \mathbf{v}_2 &=& \mathbf{0}\\ (\mathbf{p}_2 - \mathbf{p}_1) \times \mathbf{v}_2 &=& t(\mathbf{v}_1 \times \mathbf{v}_2)\\ t &=& \frac{|(\mathbf{p}_2 - \mathbf{p}_1) \times \mathbf{v}_2|}{|\mathbf{v}_1 \times \mathbf{v}_2|} \end{array} \]

好了，现在我们求出了标量 \(t\)，接下来用 \(\mathbf I=\mathbf p_1+t\mathbf v_1\) 这个式子计算出交点 \(I\) 的坐标即可。

顺便一提，这种“将点和向量统一表示”的思想在计算机图形学中有很重要的应用，即齐次坐标。

代码

首先我们需要写一个向量类。

注意，代码中的 cross 函数求的是向量积的模，所以返回的是个标量。

//二维向量
struct Vec
{
    double x, y;
    Vec() = default;
    Vec(double x, double y) : x(x), y(y) {}
    double len2() const { return x * x + y * y; }
    double len() const { return sqrt(len2()); }
    Vec operator+(const Vec &b) const { return Vec(x + b.x, y + b.y); }
    Vec operator-(const Vec &b) const { return Vec(x - b.x, y - b.y); }
    Vec operator*(double t) const { return Vec(x * t, y * t); }
    Vec operator/(double t) const { return Vec(x / t, y / t); }
    Vec operator-() const { return Vec(-x, -y); }
};

//向量积的模
double cross(const Vec &a, const Vec &b) { return a.x * b.y - b.x * a.y; }

求解两直线交点的代码。代码相当简洁，而且可以应对包括直线斜率无穷大在内的所有情况。

//求解两直线交点
//p1、v1 用于表示直线 1，p2、v2 用于表示直线 2
Vec intersection(const Vec &p1, const Vec &v1, const Vec &p2, const Vec &v2)
{
    double t = cross((p2 - p1), v2) / cross(v1, v2);
    return p1 + v1 * t;
}