线性判别分析（Linear Discriminant Analysis, LDA）

一、线性判别器的问题分析

线性判别分析（Linear Discriminant Analysis, LDA）是一种经典的线性学习方法，在二分类问题上亦称为 "Fisher" 判别分析。与感知机不同，线性判别分析的原理是降维，即：给定一组训练样本，设法将样本投影到某一条直线上，使相同分类的点尽可能地接近而不同分类的点尽可能地远，因此可以利用样本点在该投影直线上的投影位置来确定样本类型。

二、线性判别器的模型

还是假定在 \(p\) 维空间有 \(m\) 组训练样本对，构成训练集 $T = { (x_{1}, y_{1}), (x_{2}, y_{2}),...,(x_{n}, y_{n})} $，其中 \(x_{i} \in R^{1 \times p}\)，\(y_{i}\in \{-1, +1\}\)，以二维空间为例，在线性可分的情况下，所有样本在空间可以描述为：

我们的目的就是找到一个超平面 \(\Phi: b+w_{1}x_{1}+w_{2}x_{2}+..+w_{n}x_{n}=0\)，使得所有的样本点满足 “类内尽可能接近，类外尽可能遥远"。那么我们用类内的投影方差来衡量类内的接近程度，用类间的投影均值来表示类间的距离。这里，我们另 \(w\) 代表投影方向，如下图所示，

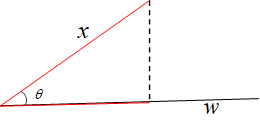
在这里，\(x,w\) 均为 \(p \times 1\) 的列向量，那么根据投影定理，\(x\) 在 \(w\) 上的投影 \(p\) 既有方向又有距离，那么：

\(p\) 与 \(w\) 同方向，表示为：\(\dfrac{w}{||w||}\)； \(p\) 的长度为：\(||x||cos\theta = ||x||\dfrac{x \cdot w}{||w||\quad||x||} = \dfrac{x \cdot w}{||w||}\)

由于 \(w\) 的长度不影响投影结果，因此我们为了简化计算，设置 \(||w||=1\)，只保留待求 \(w\) 的方向：\(||p|| = x \cdot w = w^{T}x\)

2.1 类间投影均值

我们假设用 \(u_{0}\)，\(u_{1}\) 分别表示第1，2类的均值，那么：

\[u_{0} = \dfrac{1}{m} \sum_{i=1}^{m}x_{i},\quad u_{1} = \dfrac{1}{n} \sum_{i=1}^{n}x_{i} \]

所以，第一，二类均值在 \(w\) 方向上的投影长度分别表示为：\(w^{T}u_{0}\)，\(w^{T}u_{1}\)

2.2 类内投影方差

根据方差的计算公式，第一类的类内投影方差可以表示为：

\[z_{0} = \dfrac{1}{n} \sum_{i=1}^{n}(w^{T}x_{i}-w^{T}u_{0})^{2}=\dfrac{1}{n} \sum_{i=1}^{n}(w^{T}x_{i}-w^{T}u_{0})(w^{T}x_{i}-w^{T}u_{0})^T \]

即：

\[z_{0} = \dfrac{1}{n} \sum_{i=1}^{n}w^{T}(x_{i}-u_{0})(x_{i}-u_{0})^{T}w = w^{T}[\dfrac{1}{n} \sum_{i=1}^{n}(x_{i}-u_{0})(x_{i}-u_{0})^{T}]w \]

如下图所示：

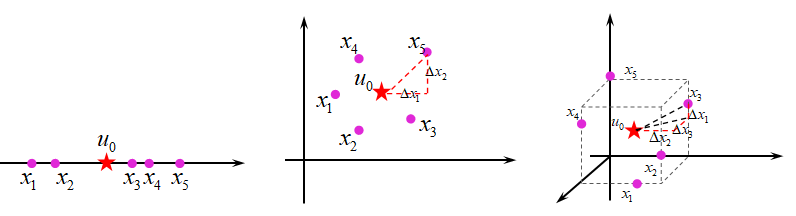
当 \(x_{i}, u_{0}\) 都是一维时， 式子 \(\dfrac{1}{n} \sum_{i=1}^{n}(x_{i}-u_{0})(x_{i}-u_{0})^{T}\) 就表示所有输入 \(x_{i}\) 的方差；

当 \(x_{i}, u_{0}\) 都是二维时， 式子 \(\dfrac{1}{n} \sum_{i=1}^{n}(x_{i}-u_{0})(x_{i}-u_{0})^{T}\) 就表示：

\[\dfrac{1}{n} \sum_{i=1}^{n}\begin{bmatrix}x_{11}-u_{01} \\x_{12}-u_{02}\end{bmatrix} \begin{bmatrix} x_{11}-u_{01}\quad x_{12}-u_{02}\end{bmatrix} = \dfrac{1}{n} \sum_{i=1}^{n}\begin{bmatrix} (x_{11}-u_{01})^{2}\quad (x_{11}-u_{01})(x_{12}-u_{02})\\ (x_{12}-u_{02})(x_{11}-u_{01})\quad (x_{12}-u_{02})^{2} \end{bmatrix} \]

其中：\(u_{01}\) 表示第一类集合中在第一个维度上的均值，\(u_{01}\) 表示第一类集合中在第二个维度上的均值，\(x_{11}\) 表示第一类集合中第一个维度的坐标值，\(x_{12}\) 表示第一类集合中第二个维度的坐标值

综上：当 $x_{i}, u_{0}$ 都是 $p$ 维时， 式子 $\dfrac{1}{n} \sum_{i=1}^{n}(x_{i}-u_{0})(x_{i}-u_{0})^{T}$ 表示 $p$ 个维度之间的协方差矩阵，我们用符号 $M_{0}$ 表示。因此（3）可以写成： $$ z_{0} = w^{T}M_{0}w $$ 同理可以得到：$z_{1} = w^{T}M_{1}w$。

我们设 \(J(w)\) 为最终的损失函数，那么满足 ”类内方差最小，类间均值最大“ 的 最大化\(J(w)\) 可以表示为：

\[J(w) = \dfrac{||w^{T}u_{0}-w^{T}u_{1}||^{2}}{z_{0}+z_{1}} = \dfrac{w^{T}(u_{0}-u_{1})(u_{0}-u_{1})^{T}w}{w^{T}(M_{0}+M_{1})w} \]

借用西瓜书的符号，我们定义类间散度矩阵：\(S_{b} = (u_{0}-u_{1})(u_{0}-u_{1})^{T}\)，类内散度矩阵：\(S_{w} = M_{0}+M_{1}\)，于是式 (6) 可以重写为：

\[J(w) = \dfrac{w^{T}S_{b}w}{w^{T}S_{w}w} \]

三、线性判别器的求解

由于 \(w\in R^{p \times 1}, S_{b},S_{w} \in R^{p \times p}\)，因此：\(J(w) \in R^{1 \times 1}\)，所以（7）可以写成：\(J(w) = {w^{T}S_{b}w}{(w^{T}S_{w}w)^{-1}}\)

根据我们之前的讲述：矩阵求导 - ZhiboZhao - 博客园 (cnblogs.com)

\[\dfrac{\partial J(w)}{\partial w} = 2S_{b}w{(w^{T}S_{w}w)^{-1}} + {(w^{T}S_{b}w)}(-1){(w^{T}S_{w}w)^{-2}} \times 2S_{w}w = 0 \]

可以解得：

\[S_{b}w = \dfrac{w^{T}S_{w}w}{w^{T}S_{w}w}S_{b}w \]

即：

\[w = \dfrac{w^{T}S_{b}w}{w^{T}S_{w}w}S_{w}^{-1}S_{b}w \]

由于我们主要关心的是 \(w\) 的方向，因此可以简化为：\(w = S_{w}^{-1}S_{b}w = S_{w}^{-1}(u_{0}-u_{1})(u_{0}-u_{1})^{T}w\)

又因为 \((u_{0}-u_{1})^{T}w\) 也是一个标量，因此，最终的结果为：\(w = S_{w}^{-1}(u_{0}-u_{1})\)

由于 \(S_{w}\) 是实对称矩阵，因此一定存在矩阵 \(U,V\)，使得：\(S_{w} = U diag(\lambda_{1},\lambda_{2},...,\lambda_{p}) V^{T}\)，所以最后的结果为：

\[w = V diag(\lambda_{1},\lambda_{2},...,\lambda_{p})^{-1} U^{T} (u_{0}-u_{1}) \]