zcash pow equihash算法详解

1 综述

1.1 简介

Equihash是一种基于广义生日问题（Generalized Birthday Problem）的内存密集型工作量证明（PoW）算法，算法核心目标是抵抗 ASIC 专用挖矿设备，让普通GPU/CPU更易参与挖矿，同时保证安全性与效率。其最著名的应用是 Zcash（主网参数 n=200, k=9），也被 ZenCash、Horizen 等加密货币采用。

1. 普通生日问题

在一个房间里，至少需要有多少人，才能使得“至少有两个人生日相同”的概率大于50%？

通常通过计算“所有人生日都不同”的互补事件概率来求解。

假设：

一年有365天（忽略润年）

每个人的生日在365天中是等可能的

生日之间相互独立

计算过程：

设房间里有n个人，则

第1个人的任取一天都不会出现生日相同（碰撞）的情况，所以不同的概率是1；

第2个人只有生日和第1个人生日不同时才能满足生日不同，所以与之前人不同的概率是364/365；

第3个人要满足和前两个人都生日都不同才行，所以与之前人不同的概率是363/365；

...

第n个人与前n−1个人生日都不同的概率是(365-(n-1))/365；

所以，所有人生日都不同的概率p(n)为：

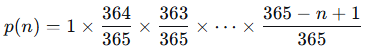
那么，至少有两个人生日相同的概率 P(n)就是：

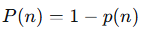
著名结论：

当n=23时：

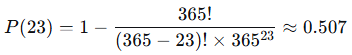
也就是说，只需要23个人，至少两人生日相同的概率就超过了50%。当n=57时，这个概率会超过99%。

在密码学中的应用（生日攻击）：

在密码学中，生日问题揭示了哈希函数碰撞的概率。假设一个哈希函数有N中可能的输出（比如N=2^m），那么只需要计算大约sqrt(N)次哈希，就有相当大的概率找到两个不同的输入产生相同的输出（即发生碰撞）。

2. 广义生日问题

“至少需要有多少人，才能使得‘至少有一组k个人生日相同’的概率超过50%？”

普通生日问题是广义生日问题在k=2时的特例。例如：k=3时，至少有三个人生日相同；k=4时，至少有四个人生日相同。

这个问题比普通生日问题复杂得多，没有简单的闭合公式，通常需要近似或者数值计算。

解决广义生日问题的一个著名近似：要使一组k个人共享同一个生日的概率超过50%，大约需要的人数为：

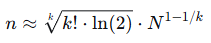
其中N是可能的天数（例如365），k是要求的人数，还以N=365为例：

k=2（普通生日问题）：

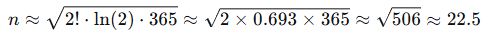
这与之前精确计算的23人非常接近。

k=3：

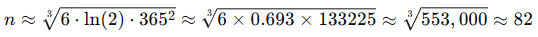
这意味着大约需要82人，才有超过50%的概率找到至少三个人生日相同。

3. Equihash中广义生日问题

在Equihash算法中涉及的广义生日问题可以归纳如下：

1）由区块头数据通过Blake2b哈希生成长度为N的哈希串列表；

2）在列表中找到2^k个哈希串的异或结果为 0（注意这里异或为0，并不是表示2^k个完全相同的哈希串，这里的异或为零是更宽松的组合约束）；

3）最终解为满足条件的2^k个哈希值的索引组合（最终需转换为字节流，作为区块的 nSolution 字段）。

1.2 算法及数据结构

tromp给出equihash算法工程实现：

https://github.com/tromp/equihash

1. 关键参数

在Zcash中使用的参数N=200，K=9，这意味着：

N（Width）：产生的哈希值总宽度为200bits（50字节）；

K（Steps）：算法分为9轮（实际上是K步碰撞），对应算法输出的2⁹个索引；

HEADERNONCELEN：140字节，Blake2b哈希函数的输入数据长度，通常由Block Header（区块头）+ Nonce（随机数）组成。在Zcash中，这个总长度通常固定为140字节；

NDIGIT：K+1=10，在算法实现中会将N位哈希输出切分成10个小块（Digit）分轮逐层解决；

DIGITBITS：N/NDIGITS=200/10=20bits，每个Digit的位宽（也就是每一轮碰撞的长度L）；

PROOFSIZE：1<<K=512，解包含的索引数量，即最终需要提交这512个索引作为工作量证明；

BASE：1<<DIGITBITS=2²⁰=1048576，碰撞空间大小，因为每一轮要检查20bits的碰撞，那么就有2²⁰种可能的数据，可以把该值想象成有1048576个“理论上的抽屉”，后续需要把初始哈希串放入这些抽屉里；

NHASHES：2*BASE=2097152（200百万），算法第一步生成的初始哈希串总数，如果只生成 BASE个数据，那么平均每个抽屉里只有1个数据，这时无法和其他串发生碰撞（找不到配对），算法就无法继续，为了保证每一轮都能顺利进行，需要让每个“理论抽屉”里平均至少有2个数据；

HASHESPERBLAKE：512/N=2，标准Blake2b输出是512bits，equihash算法中需要的是200bits的哈希串，所以512bits可以切出2个200bits哈希串，剩下的112位被丢弃；

HASHOUT：HASHESPERBLAKE*N/8=50字节，Blake2b算法输出50字节即可（2x200bits）；

在Tromp的Equihash工程实现中，引入了Bucket（桶）和Slot（槽）两个用于管理内存和数据的关键概念，在Equihash算法中，有几百万个数据需要处理，如果把它们放在一个大数组里排序，速度太慢，所以要使用“分治法”。

Bucket (桶) —— 数据的“大分组”

定义：Bucket 是内存中的一块逻辑区域，用于存放具有相同前缀（Prefix）的哈希串。

决定因素：BUCKBITS，如果 BUCKBITS = 10，说明有2¹⁰ = 1024个桶。数据的前10位决定了它去哪个桶。

物理形态：在 C++ 代码中，Bucket 通常不是一个复杂的 class，而仅仅是计算出的内存偏移量 (Offset)。

Bucket_0 的内存地址 = 起始地址 + 0

Bucket_1 的内存地址 = 起始地址 + (每个桶的大小)

作用：减少碰撞搜索范围。数据一旦进入不同的桶，它们在当前轮次绝对不可能碰撞，所以后续计算完全不需要考虑跨桶的情况，这对 CPU 缓存非常友好。

Slot (槽) —— 数据的“具体容器”

定义：Slot是Bucket内部的一个最小存储单元。

决定因素：SLOTBITS，如果SLOTBITS = 12，说明每个桶最多能容纳2¹² = 4096个数据（Slot）。

存储内容：Slot里不存完整的哈希值（浪费空间），只存必要的压缩信息：

1）索引 (Index)：这组数据最初是来自哪个（或哪些）原始输入。

2）剩余位 (Rest Bits)：除去桶编号（前缀）后，剩下的哈希位。

固定大小 (Flat Memory)：在Tromp的代码中，并没有使用链表（Linked List）来动态增加 Slot，因为指针跳转太慢。

他预先分配了固定大小的内存：总内存 = 桶数量 × 每个桶的Slot数量 × Slot大小。

风险：如果运气不好，某个哈希前缀出现太多次，导致对应桶的数据超过了 Slot 的上限，就会发生溢出 (Overflow)，这部分多余的数据通常会被丢弃（为了性能牺牲一点点求解概率）。

结合以上内容，给出和桶和槽相关参数

RESTBITS：10，对于20位的Digit来说，前10位用于确定它属于哪个Bucket，则还有10位是剩余的数据位；

BUCKBITS：DIGITBITS-RESTBITS=10，2¹⁰是桶的总数，Digit前10位确定“桶号”；

SLOTBITS：RESTBITS+1+1=12，这个参数定义了一个桶最多能装多少个数据（Slot），总数据量是NHASHES=2x2²⁰，桶的总数是2¹⁰，则平均每个桶会分到2x2²⁰/2¹⁰=2¹¹=2048个数据，11正好对应RESTBITS+1，而定义中的第2个+1是除于安全冗余考虑，由于哈希分布是随机的，有的桶数据少，有的桶数据多。为了防止数据多的桶溢出（Overflow），这里多给了1位空间（即容量翻倍），允许一个桶最多装2¹² = 4096个数据。

2. Wagner算法

Equihash要求找到2^K个不同的输入x_i，使得：

H(x₁) XOR H(x₂) XOR ... XOR H(x_2^k) = 0

例如在K=9时，需要有512个不同索引的哈希XOR = 0。此时直接暴力找512个XOR=0的组合不现实，因此引入了Wagner's algorithm。

Wagner的思路非常简单但很强大：

把“求2^K个数XOR=0”转换成K轮“两两XOR消除部分前缀”的逐层合并。

首先对备选哈希数据按前缀不同进行分桶，每个桶中都是有相同前缀的哈希数据（相当于抹掉部分哈希前缀位），之后流程结构如下：

最终XOR被零掉的bit = (k+1) × N/(k+1) = N ⇒ 全部 XOR 为 0。在Wagner算法中每轮处理主要做以下操作：

1）依次处理每个桶，桶内为以消除部分相同前缀的哈希串；

2）进一步查找桶内具有特定位相同前缀的哈希对（能产生碰撞的两个哈希）；

3）将碰撞哈希对进行异或产生新的哈希数据（会消除相同前缀），同时将之前桶号及索引（桶内位置）进行数据组合（最后进行解回溯时使用）；

4）根据异或哈希数据按特定位前缀再次进行分桶（前缀相同分入到相同桶）；

再上述过程中查找碰撞对儿其实就是在搜索前缀相同的哈希，保证之后的异或操作会消除相应的bit，而之后根据哈希前缀进行分桶也是类似，也是保证在同一个桶内的哈希都是前缀相同的，便于在进行多线程处理时都是在同一桶内进行的。

2 源码解析

2.1 内存结构

1. 关键宏定义

首先看如下宏定义：

#if RESTBITS < 8
// can't save much memory in such small buckets
#define SAVEMEM 1
#else
// an expected size of at least 512 has such relatively small
// standard deviation that we can reduce capacity with negligible discarding
// this value reduces (200,9) memory to under 144MB
// must be under sqrt(2)/2 with -DCANTOR
#define SAVEMEM 9/14        // 容量缩减因子
#endif // RESTBITS == 4

#endif // ifndef SAVEMEM

static const u32 NBUCKETS = 1<<BUCKBITS;    // number of buckets
static const u32 BUCKMASK = NBUCKETS-1;     // corresponding bucket mask
static const u32 SLOTRANGE = 1<<SLOTBITS;   // default bucket capacity
static const u32 SLOTMASK = SLOTRANGE-1;    // corresponding SLOTBITS mask
static const u32 SLOTMSB = 1<<(SLOTBITS-1); // most significat bit in SLOTMASK
static const u32 NSLOTS = SLOTRANGE * SAVEMEM; // number of slots per bucket
static const u32 NRESTS = 1<<RESTBITS;      // number of possible values of RESTBITS bits
static const u32 MAXSOLS = 8;               // more than 8 solutions are rare

SAVEMEM定义内存容量缩减因子，根据桶内数据密度，在保证求解率的前提下，减少每个桶的槽位（Slot）数量，从而降低整体内存占用。默认的SLOTRANGE (2¹²=4096) 包含了大量的冗余空间。当RESTBITS足够大（>=8）时，意味着每个桶的元素足够多，可以安全地将容量从默认的SLOTRANGE缩减到9/14，以节省内存。

2. 存储结构体定义

// each bucket slot occupies a variable number of hash/tree units,
// all but the last of which hold the xor over all leaf hashes,
// or what's left of it after stripping the initial i*n 0s
// the last unit holds the tree node itself
// the hash is sometimes accessed 32 bits at a time (word)
// and sometimes 8 bits at a time (bytes)
union htunit {
  tree tag;
  tree_t word;
  uchar bytes[sizeof(tree_t)];
};

#define WORDS(bits)    ((bits + TREEBITS-1) / TREEBITS)
#define HASHWORDS0 WORDS(WN - DIGITBITS + RESTBITS)
#define HASHWORDS1 WORDS(WN - 2*DIGITBITS + RESTBITS)

// A slot is up to HASHWORDS0 hash units followed by a tag
typedef htunit slot0[HASHWORDS0+1];
typedef htunit slot1[HASHWORDS1+1];
// a bucket is NSLOTS treenodes
typedef slot0 bucket0[NSLOTS];
typedef slot1 bucket1[NSLOTS];
// the N-bit hash consists of K+1 n-bit "digits"
// each of which corresponds to a layer of NBUCKETS buckets
typedef bucket0 digit0[NBUCKETS];
typedef bucket1 digit1[NBUCKETS];
typedef au32 bsizes[NBUCKETS];

1）htunit类型

htunit联合体类型是Equihash求解器中存储数据的最小通用单元，联合体的特性是，它内部的所有成员共享一块内存空间，这意味着tag、word和bytes都是对同一32/64位内存的不同解释。

引入联合体的目的：提高代码的灵活性和性能。当进行复杂的位操作时，使用 word；当处理索引时，使用tag；当进行底层内存操作时，使用 bytes。

2）槽定义

Slot是存储一个碰撞数据项的容器，它是一个定长数组，用于存储哈希数据和树节点信息。

typedef htunit slot0[HASHWORDS0 + 1];

大小：HASHWORDS0 + 1个htunit，位数WN - DIGITBITS + RESTBITS = 200 - 20 + 10 = 190，则HASHWORDS0值为6个WORDS，再+1，最终为7个WORDS。

用途：用于第0轮的输出，即digit0输出的存储结构。

结构：数组的前HASHWORDS0个单元存储压缩后的哈希数据；最后一个单元（+1）存储该数据项的树节点tag。

即slot0对应的类型为大小为7个htunit的数组。

typedef htunit slot1[HASHWORDS1 + 1];

大小：HASHWORDS1 + 1 个 htunit，位数WN - 2*DIGITBITS + RESTBITS = 200 - 2*20 + 10 = 170，则HASHWORDS1值也为6个WORDS，再+1，最终也为7个WORDS。

用途：用于第1轮的输出，即digit1输出的存储结构。

压缩：由于HASHWORDS1 <= HASHWORDS0（因为第1轮又消除了20位），slot1通常比slot0更小，从而可能会节省些许内存（在N=200情况下这两个值是相同的）。

在后续的乒乓操作中会复用这两个内存结构。

3）桶定义

桶是相同类型槽的集合。

typedef slot0 bucket0[NSLOTS];

保存slot0类型数据的数组型桶结构，它是包含NSLOTS=2633个slot0类型数据的定长数组。

typedef slot1 bucket1[NSLOTS];

保存slot1类型数据的数组型桶结构，它是包含NSLOTS=2633个slot1类型数据的定长数组。

4）内存堆定义

digit结构定义了整个内存堆，对应于乒乓机制的中一个“球台”。

typedef bucket0 digit0[NBUCKETS];

用于存储初始轮次数据的内存堆结构（通常是乒乓机制中的heap0），它由NBUCKETS=1024个bucket0组成，其中每个桶都使用slot0存储数据。

typedef bucket1 digit1[NBUCKETS];

用于存储后续轮次数据的内存堆结构（通常是乒乓机制中的heap1），它由NBUCKETS=1024个bucket1组成，其中每个桶都使用slot1存储数据。

5）辅助结构

typedef au32 bsizes[NBUCKETS];

含义：桶大小数组（Bucket Sizes）。

用途：au32通常是原子32位无符号整数。这个数组用于在多线程环境中安全地追踪每个桶当前实际存储了多少个数据项。这是多线程无锁写入的关键：每个线程写入数据后，原子性地增加对应桶的计数器。

3. 内存分配

在进行碰撞检测前首先进行必要的内存分配，主要内容如下：

void alloctrees() {
    static_assert(2*DIGITBITS >= TREEBITS, "needed to ensure hashes shorten by 1 unit every 2 digits");
    heap0 = (bucket0 *)alloc(NBUCKETS, sizeof(bucket0));
    heap1 = (bucket1 *)alloc(NBUCKETS, sizeof(bucket1));
}

equi(const u32 n_threads) {
    static_assert(sizeof(htunit) == sizeof(tree_t), "");
    static_assert(WK&1, "K assumed odd in candidate() calling indices1()");
    nthreads = n_threads;
    //const int err = pthread_barrier_init(&barry, NULL, nthreads);
    //assert(!err);
    hta.alloctrees();
    nslots = (bsizes *)hta.alloc(2 * NBUCKETS, sizeof(au32));
    sols   =  (proof *)hta.alloc(MAXSOLS, sizeof(proof));
}

首先调用alloctrees函数分配两个乒乓堆heap0和heap1，之后给用于维护两个乒乓堆中各个桶中slots个数的nslots成员变量分配内存，最后分配8个（最多求8个解）大小为proof的sols成员变量分配内存。 

2.2 首轮函数digit0

首轮函数通过index附加调用blake2b哈希函数，将产生的哈希结果填充到heap0中，其内容如下：

void digit0(const u32 id) {
    htlayout htl(this, 0);
    const u32 hashbytes = hashsize(0);
    uchar hashes[NBLAKES * 64];
    blake2b_ctx state0 = blake_ctx;  // local copy on stack can be copied faster
    for (u32 block = id; block < NBLOCKS; block += nthreads) {
#if NBLAKES == 4
#ifdef ASM_BLAKE
      Blake2Run4(hashes, (void *)&state0, NBLAKES * block);
#else
      blake2bx4_final(&state0, hashes, block);
#endif
#elif NBLAKES == 8
      blake2bx8_final(&state0, hashes, block);
#elif NBLAKES == 1
      blake2b_ctx state = state0;  // make another copy since blake2b_final modifies it
      u32 leb = htole32(block);
      blake2b_update(&state, (uchar *)&leb, sizeof(u32));
      blake2b_final(&state, hashes);
#else
#error not implemented
#endif
      for (u32 i = 0; i<NBLAKES; i++) {
        for (u32 j = 0; j<HASHESPERBLAKE; j++) {
          const uchar *ph = hashes + i * 64 + j * WN/8;
          // figure out bucket for this hash by extracting leading BUCKBITS bits
#if BUCKBITS <= 8
          const u32 bucketid = (u32)(ph[0] >> (8-BUCKBITS));
#elif BUCKBITS > 8 && BUCKBITS <= 16
          const u32 bucketid = ((u32)ph[0] << (BUCKBITS-8)) | ph[1] >> (16-BUCKBITS);
#elif BUCKBITS > 16
          const u32 bucketid = ((((u32)ph[0] << 8) | ph[1]) << (BUCKBITS-16)) | ph[2] >> (24-BUCKBITS);
#else
#error not implemented
#endif
          // grab next available slot in that bucket
          const u32 slot = getslot0(bucketid);
          if (slot >= NSLOTS) {
            bfull++; // this actually never seems to happen in round 0 due to uniformity
            continue;
          }
          // location for slot's tag
          htunit *s = hta.heap0[bucketid][slot] + htl.nexthtunits;
          // hash should end right before tag
          memcpy(s->bytes-hashbytes, ph+WN/8-hashbytes, hashbytes);
          // round 0 tags store hash-generating index
          s->tag = tree((block * NBLAKES + i) * HASHESPERBLAKE + j);
        }
      }
    }
}

以NBLAKES=1时为例进行分析，函数中第2行定义htl变量用于统一管理每轮digit处理时的相关参数，如其中成员变量prevhtunits用于指定上一个slot数据对应的htunit数组在内存中的位置，而nexthtunits用于指定下一个slot数据对应的htunit数组在内存中的位置；第3行给出了该轮有效哈希数据字节数，由于200bit中有10bit体现在桶编号里，所以这里190bit对应字节数是24；之后第6行for循环依次处理每个哈希输出，循环次数为NBLOCKS = (NHASHES+HASHESPERBLOCK-1)/HASHESPERBLOCK=2x2²⁰/2=2²⁰；第24行处for循环对应的逻辑是每个哈希输出结果可以产生两个slot数据；第30行将哈希输出的最低10bit作为桶编号；第37行根据桶编号取出相应的可用slot；第43~47行将剩余的哈希数据（去除10bit桶号）存储到slot中，并用tag记录index，具体来说对于slot对应的htunits[7]数组，索引[0]到[5]存储剩余哈希数据，索引[6]存储树节点tag索引。该轮执行完毕后所有桶存储于heap0，桶中的slot数据内存结构如下图：

2.3 次轮函数digit1

在调用完digit0函数后，每个桶中的哈希数据是原始哈希输出前10bit（Digit0前10位）结果相同的哈希的剩余哈希数据，在此轮要找到两个Digit0剩余10bit也相同的两两哈希对儿，并将它们的哈希数据进行异或，根据异或结果对应的Digit1前10bit进行再次分桶操作，函数内容如下：

void digit1(const u32 id) {
    htalloc heaps = hta;
    collisiondata cd;
    for (u32 bucketid=id; bucketid < NBUCKETS; bucketid += nthreads) {
      cd.clear();
      slot0 *buck = heaps.heap0[bucketid];      // 要处理的输入桶，桶中所有的slot中数据前10bit相同都是bucketid（bucketid已经确定该10bit值，所以该10bit并没有在数据中进行存储）
      u32 bsize   = getnslots0(bucketid);       // 当前桶实际使用的Slot数量，即当前桶中实际存储了多少个slot的数据，后续要检测将会发生碰撞的slot对儿
      for (u32 s1 = 0; s1 < bsize; s1++) {      // 遍历当前桶内的每一个Slot，查找会和该Slot发生碰撞的Slot
        const htunit *slot1 = buck[s1];
        cd.addslot(s1, htobe32(slot1->word) >> 20 & 0x3ff);     // 提取10位RESTBITS，将Slot索引(s1)和这10位RESTBITS存入cd结构中
        for (; cd.nextcollision(); ) {
          const u32 s0 = cd.slot();
          const htunit *slot0 = buck[s0];       // 取得与slot1发生碰撞的slot0
          if (slot0[5].word == slot1[5].word) {
            hfull++;
            continue;
          }
          u32 xorbucketid = htobe32(slot0->word ^ slot1->word) >> 10 & BUCKMASK;
          const u32 xorslot = getslot1(xorbucketid);
          if (xorslot >= NSLOTS) {
            bfull++;
            continue;
          }
          u64 *x  = (u64 *)heaps.heap1[xorbucketid][xorslot];
          u64 *x0 = (u64 *)slot0, *x1 = (u64 *)slot1;
          *x++ = x0[0] ^ x1[0];
          *x++ = x0[1] ^ x1[1];
          *x++ = x0[2] ^ x1[2];
          ((htunit *)x)->tag = tree(bucketid, s0, s1);
        }
      }
    }
}

第3行定义collisiondata类型变量cd用于检测碰撞；第4行for循环依次处理每个桶；第6~7行首先获取当前桶数据指针，接下来获取当前桶中slot个数；第8行的for循环依次遍历每个slot，借助cd变量检测是否会发生碰撞；第9~10行以循环下标为索引取出slot1，并将其添加到cd碰撞检测器中；第11行for循环只要碰撞检测器中还存在碰撞，则依次处理碰撞；第12~13行取出和slot1发生碰撞的slot索引，并将相应slot0取出；接下来第14~17行通过比较两个slot的最后一个word来判断两个slot是不是“重复数据”（这种情况一般不会发生），如果是则忽略当前碰撞；第18行将slot0和slot1的哈希数据中第一个word进行异或，并取低10bit数据（即Digit1的低10bit）为下一轮的桶编号；第19~23行从heap1中获取该桶编号相应可用slot索引，如果溢出则忽略当前碰撞；接下来第24~28行先根据桶编号及slot索引获取相应的htunit数组内存存储空间，然后将slot0和slot1对应的哈希数据异或后存储到htunit数组的[0]到[5]对应的元素中（即4*6=8*3=24字节内存中）；第29行将碰撞对儿的原始桶编号和slot索引组成tree结构放入到htunit数组索引[6]元素中。该轮执行完毕后所有桶存储于heap1，桶中的slot数据内存结构如下图：

图中bucketid对应digit0之后输出heap0中相应的桶编号，s0和s1对应相应桶中的slot索引。

2.4 函数digit2及digitK

经过digit1轮处理后，heap1中每个桶内存储的都是异或后Digit0为全零且Digit1低10bit值相同的哈希对儿数据异或结果，在digit2函数中将进一步检测并处理两两哈希对儿异或结果之间碰撞，函数内容如下：

void digit2(const u32 id) {
    htalloc heaps = hta;
    collisiondata cd;
    for (u32 bucketid=id; bucketid < NBUCKETS; bucketid += nthreads) {
      cd.clear();
      slot1 *buck = heaps.heap1[bucketid];
      u32 bsize   = getnslots1(bucketid);
      for (u32 s1 = 0; s1 < bsize; s1++) {
        const htunit *slot1 = buck[s1];
        cd.addslot(s1, htobe32(slot1->word) & 0x3ff);
        for (; cd.nextcollision(); ) {
          const u32 s0 = cd.slot();
          const htunit *slot0 = buck[s0];
          if (slot0[5].word == slot1[5].word) {
            hfull++;
            continue;
          }
          u32 xor1 = slot0[1].word ^ slot1[1].word;
          u32 xorbucketid = htobe32(xor1) >> 22;
          const u32 xorslot = getslot0(xorbucketid);
          if (xorslot >= NSLOTS) {
            bfull++;
            continue;
          }
          htunit *xs = heaps.heap0[xorbucketid][xorslot];
          xs++->word = xor1;
          u64 *x = (u64 *)xs, *x0 = (u64 *)slot0, *x1 = (u64 *)slot1;
          *x++ = x0[1] ^ x1[1];
          *x++ = x0[2] ^ x1[2];
          ((htunit *)x)->tag = tree(bucketid, s0, s1);
        }
      }
    }
}

除了部分细节digit2函数大体流程和digit1非常类似，如第10行在向碰撞检测器中添加slot时，slot1->word最低10bit对应的是digit1的高10bit值；第18行进一步对两个slot索引[1]位置的哈希值进行异或；第25~29行进一步只对slot剩余部分的哈希数据进行异或操作（前面的哈希数据经过碰撞已经全部为0）。digit2执行完毕后，会更新存储在heap0的各桶中内容，需要注意的是该轮处理过程中仅仅更新了slot中htunit数组的前6个word内容，在digit0中产生的tag并没有被改动（最后进行求解追溯时需要利用这里的数据），完美的实现了内存复用。

 

其他digitx处理过程类似不再详细进行说明，接下来看一下最后一个digitK（digit9）处理函数：

void digitK(const u32 id) {
    collisiondata cd;
    htlayout htl(this, WK);
    u32 nc = 0;
    for (u32 bucketid = id; bucketid < NBUCKETS; bucketid += nthreads) {
      cd.clear();
      slot0 *buck = htl.hta.heap0[bucketid];   // assume WK odd
      u32 bsize   = getnslots0(bucketid);      // assume WK odd
      for (u32 s1 = 0; s1 < bsize; s1++) {
        const htunit *slot1 = buck[s1];
        cd.addslot(s1, htl.getxhash0(slot1));  // assume WK odd
        for (; cd.nextcollision(); ) {
          const u32 s0 = cd.slot();
          const htunit *slot0 = buck[s0];
          // there is only 1 word of hash left
          if (htl.equal(slot0, slot1) && slot0[1].tag.prob_disjoint(slot1[1].tag)) {
            candidate(tree(bucketid, s0, s1)); // so a match gives a solution candidate
            nc++;
          }
        }
      }
    }
    // printf(" %d candidates ", nc);  // this gets uncommented a lot for debugging
}

首先给出在digit8函数调用完成以后slot中数据内存结构，如下图所示：

 

上图中tag_digit7表示的是在digit7处理完成后对应heap1输出，digitK函数以上图的heap0为输入（偶数轮调用输出是heap0，奇数轮调用输出是heap1，每轮调用的输入又是上一轮调用的输出，这是就所谓的内存“乒乓”机制），digitK函数中整体处理过程和其他digit处理类似，只不过由于hash数据只剩30bits完全存储在一个word中，所以已经没必要再次进行分桶操作，所以第16行直接对相应的值进行了比较（等同于异或）并判断两个slot中的tag中是否发生重叠，在Equihash的K轮碰撞过程中，要求2^K个原始输入索引必须互不相同，满足条件后产生潜在解，在candidate函数中会对潜在解做进一步检验，通过检验后才真正的产生解，具体内容可以参考candidate函数实现。

2.5 其他补充说明

1. collisiondata结构体

该结构体定义的主要内容如下：

struct collisiondata {
    // This maintains NRESTS = 2^RESTBITS lists whose starting slot
    // are in xhashslots[] and where subsequent (next-lower-numbered)
    // slots in each list are found through nextxhashslot[]
    // since 0 is already a valid slot number, use ~0 as nil value
#if RESTBITS <= 6
    typedef uchar xslot;
#else
    typedef u16 xslot;                  // 槽位索引类型
#endif
    static const xslot xnil = ~0;       // 空值/链表结尾标记，槽位索引从0开始有效，用~0表示空值
    xslot xhashslots[NRESTS];           // 散列表长度1024，其索引是10位的RESTBITS值，对应内容是具有该RESTBITS值的最新槽位索引，例如addslot(s1, xh)，则xhashslots[xh] = s1，即值xh的槽位索引是s1
    xslot nextxhashslot[NSLOTS];        // 链表指针数组长度2633，这是真正的链表结构，nextxhashslot[s]存储的是槽位s的前一个具有相同RESTBITS值的槽位索引，值是小于1024的索引数
    xslot nextslot;                     // 前一个碰撞Slot的临时索引，该值不为xnil时，表示有碰撞发生
    u32 s0;                             // 当前找到的碰撞Slot的索引
}

该结构核心内容是散列链表即散列表和链表结合的数据结构，其中xhashslots对应散列表，用于提供快速、近似O(1)时间复杂度的查找、插入和删除能力，nextxhashslot为链表，以维护元素的某种顺序（如插入顺序、访问顺序等），散列链表能够同时获取散列表的效率和链表的灵活性。仍结合digit1函数源码进行说明，第5行在使用碰撞检测器之前，会使用clear函数将xhashslots和nextxhashslot所有元素赋值为无效值xnil，第6行取出当前要处理的桶buck，第7行获取到当前桶buck中Slot的个数bsize，接下来for循环依次取出桶中的Slot，并放入到碰撞检测器，通过调用cd.addslot(s1, xh)实现，参数s1是桶buck索引，参数xh是Digit0的RESTBITS（剩余10bits）对应的值，插入函数内容如下：

void addslot(u32 s1, u32 xh) {
      nextslot = xhashslots[xh];
      nextxhashslot[s1] = nextslot;
      xhashslots[xh] = s1;
}

第2行首先根据xh获取未进行插入前的具有RESTBITS值的最新槽位索引nextslot（在插入后该值实际上是前一个具有xh值的槽位索引），第3行将nextxhashslot的s1位置赋值为最新槽位索引，第4行通过插入更新具有xh值的最新槽位索引为s1，由于该行更新第3行的值其实已经相当于是上一个具有xh值的槽位索引。

继续进行digit1函数分析，将Slot插入到碰撞检测器以后，又在第11行用检测器来循环检测新插入Slot是否和检测器中已有Slot发生碰撞，如果碰撞则取出会产生碰撞的Slot s0，并将其和新插入s1进行异或及入桶操作（这里的入桶为另一个乒乓heap中的桶），碰撞检测及取碰撞Slot函数内容如下：

bool nextcollision() const {
    return nextslot != xnil;
}
 
u32 slot() {
    nextslot = nextxhashslot[s0 = nextslot];
    return s0;
}

nextcollision函数很简单，如果插入后前一个槽位索引nextslot不是无效值，则说明插入s1槽和nextslot槽有相同插入值xh，即产生碰撞。而取碰撞槽函数slot会将碰撞槽赋值给s0返回，并更新nextslot为再上一个槽，继续进行碰撞检测。下图给出了插入4个Slot过程示意图，图中第一个是链表nextxhashslot，第二个是散列表xhashslots：

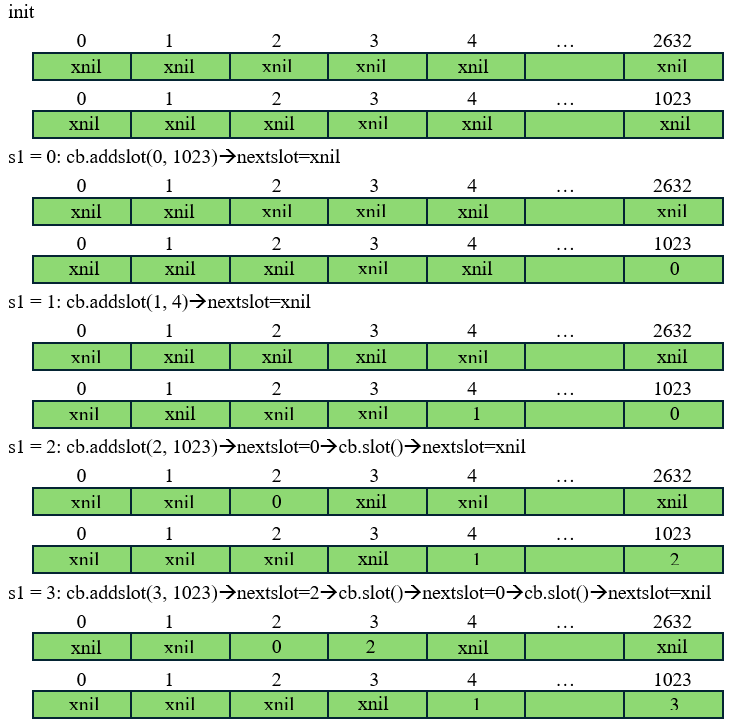
以插入cb.addslot(3, 1023)后为例，此时下一个碰撞slot索引为nextslot=2，此时将会对(3, 2)索引对对应的slot数据进行哈希异或并入乒乓桶，之后nextslot=0，说明仍存在碰撞，继续对(3, 0)索引对对应的slot数据进行哈希异或并入乒乓桶，再之后nextslot=xnil已无碰撞，此时可继续进行新的slot入检测器并判断处理操作。其实直观来看索引3，2，0对应的xh值都为1023，显而易见它们确实是有碰撞的。

2. 康托尔配对函数

康托尔配对函数是集合论与可计算性理论中的核心工具，由德国数学家格奥尔格・康托尔（Georg Cantor）提出，用于实现两个非负整数到一个非负整数的双射映射（即一一对应）。其核心价值在于证明了 “可数无穷集合的笛卡尔积仍是可数无穷”（如ℕ×ℕ与ℕ等势），为后续可数性理论、哥德尔编码、数据压缩等领域奠定了基础。在equihash算法中，每个Slot索引是12位，则存储s0需要12 bits，存储s1需要12 bits，存储Bucket ID需要10 bits，则总计需要12+12+10=34 bits，34 bits超过标准的32位整数（u32），这意味着需要用u64或者两个u32来存，将直接增大heap内存大小，还好这里巧妙地使用康托尔配对函数后，会在仅使用22 bits就可以存储下s0和s1经过康托尔映射后的值，算法中使用如下函数给出康托尔配对：

static u32 cantor(u32 s0, u32 s1) {
  return s1*(s1+1)/2 + s0;
}

u32 slotid0(u32 s1) const {
    return (bid_s0_s1 & CANTORMASK) - cantor(0,s1);
}

u32 slotid1() const {
    u32 k, q, sqr = 8*(bid_s0_s1 & CANTORMASK)+1;;
    // this k=sqrt(sqr) computing loop averages 3.4 iterations out of maximum 9
    for (k = CANTORMAXSQRT; (q = sqr/k) < k; k = (k+q)/2) ;
    return (k-1) / 2;
}

在函数中使用的配对公式（基于三角形数）如下，且有s0<s1：

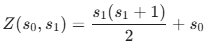
其三角形结构如下图所示：

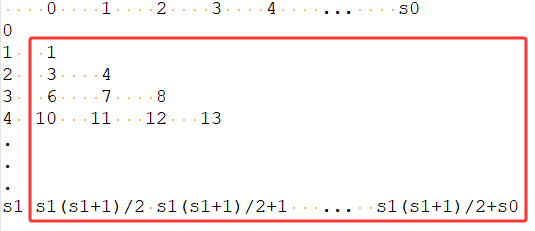
因为Slot个数是NSLOTS，所以s1最大取值为NSLOTS-1，s0最大取值为NSLOTS-2，则理论上配对最大个数为Pmax=1+2+3+...+(NSLOTS-1)=NSLOTS*(NSLOTS-1)/2，但是观察三角形结构可知，在编码公式的操作下，编码后的Z值并不是连续的，所以它必须检查最大编码值Zmax，使得Zmax<NSLOTPAIRS，而不是配对总数小于NSLOTPAIRS，根据公式可知Zmax=s1*(s1+1)/2+s0=(NSLOTS-1)*(NSLOTS-1+1)/2+(NSLOTS-2)=(NSLOTS-1) * (NSLOTS+2) / 2-1<NSLOTPAIRS，即(NSLOTS-1) * (NSLOTS+2) / 2<=NSLOTPAIRS，可以将NSLOTS=2633代入其中，可得值为0x34e98c，易见其确实是22bits。

3. candidate

正如之前已经提到过的，在该函数中会通过listindeces1函数进行回溯以求得最终解，而duped函数中会进一步进行重叠判断，以满足最初的异或要求（所有初始哈希索引互不相同），成功进行了这两种操作的解才是最终解，并将解拷贝到解数组sols中，完整函数流程如下图：

void candidate(const tree t) {
    proof prf;
    // listindices combines index tree reconstruction with probably dupe test
    if (listindices1(WK, t, prf) || duped(prf)) return; // assume WK odd
    // and now we have ourselves a genuine solution
#ifdef ATOMIC
    u32 soli = std::atomic_fetch_add_explicit(&nsols, 1U, std::memory_order_relaxed);
#else
    u32 soli = nsols++;
#endif
    // copy solution into final place
    if (soli < MAXSOLS) memcpy(sols[soli], prf, sizeof(proof));
}

4. 难度比较

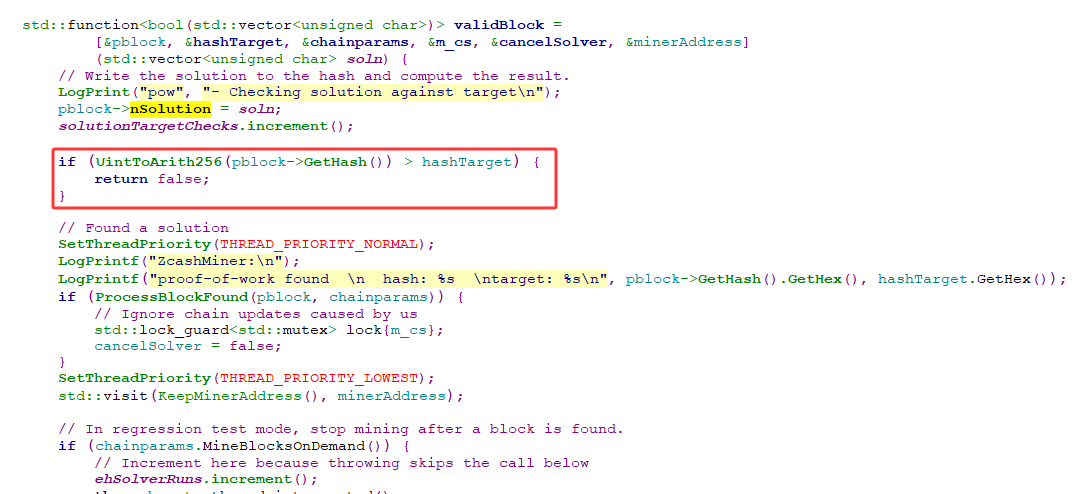
以上只是zcash pow算法中的核心函数equihash，其实和其他pow项目一样，在出块儿也会进行难度检查等常规操作，如下图所示，另外项目方在钱包源码中也给出优化版本函数EhOptimisedSolve，可以参考本文内容进行解析，这里不再详细介绍。

 

3 参考

1. https://www.zhihu.com/column/p/24450669

2. https://github.com/tromp/equihash

3. https://github.com/zcash/zcash