secp256k1算法详解五(kG点乘多梳状算法)
1 理论基础
在椭圆曲线密码学(ECC)中,kG也称标量乘法运算,即把椭圆曲线上的基点G与标量k进行相乘的运算,结果是椭圆曲线上的另一个点R=kG,其定义为k个G连续相加的结果。该运算是椭圆曲线密钥生成、加解密、签名及验证中的核心运算,所以围绕它产生了多种加速算法,这里仅对secp256k1中前后出现的两种典型算法进行说明。
1.1 窗口查表算法(Windowed lookup)
该算法是secp256k1库早期所使用的算法,其核心思想是将标量k(以256位标量为例)按bits位划分为256/bits个窗口,然后根据预计算查找表查找每个窗口值对应的点,再将每个窗口点相加即可得到最终结果R,其数学公式如下:
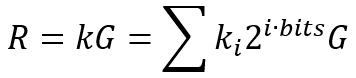
以窗口大小bits=4为例,则窗口数为256/4=64个,上述公式可以表示为:
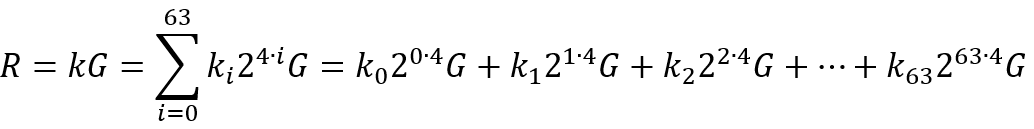
这里ki为4bit二进制数,所以每个窗口包含24=16个查找点(一个窗口对应点0G, 1G, 2G, ..., 15G),则包含16个窗口的查找表为64x16的二维数组,整个表的内存大小为64*16*sizeof(POINT),假如POINT点x,y坐标都以32字节保存,则查找表所需的内存大小为64*16*(32+32)=64KB。这里如果将bits增大到16,则每个窗口包含216=65536个查找点,窗口个数为256/16=16个,整个查找表大小为16*65536*sizeof(POINT)=64MB。
根据以上分析可知整个kG计算复杂度为O(256/bits)点加操作,例如当bits=4时,需要查找64次表再将对应结果点进行点加即可。
1.2 多梳状算法(Multi-Comb)
为了严格的对应上源码,这里也加入了盲化部分内容,即计算R=kG时不直接进行计算,而是计算R=(k - b)*G + b*G,这样是为了防止攻击者通过分析功耗、电磁辐射等侧信道信息来推测出k,从而引入随机盲化值b,对于盲化后的计算公式,b*G可以预运算获得(对应后续源码中的ge_offset,通过查表计算出(k-b)*G后要加上该值才能得到最终值kG),所以对于任意的k,其实盲化后主要计算部分是(k - b)*G。在计算该部分时,使用了有符号数字多梳状算法,该算法中定义的comb(s, P)函数是一个关键内容:
comb(s, P) = sum( (2*s[i] - 1) * 2^i * P ) for i=0..COMB_BITS-1
其中,s[i]是标量s的第i个比特值(0或1),P是椭圆曲线上点。公式中2*s[i] - 1是一个巧妙的转换:如果s[i] = 1,则2*1 - 1;如果s[i] = 0,则2*0 - 1 = -1,所以上式中对于每个比特位i,不是加上2^i*P就是减去2^i*P,这就是“有符号数字”的含义(系数是+1或-1),可以进一步将该式简化称一个更熟悉的形式:
comb(s, P) = sum( (2*s[i] - 1) * 2^i * P ) (1) = [ sum( 2*s[i]*2^i ) - sum( 2^i ) ] * P = [ 2 * sum(s[i]*2^i) - (2^COMB_BITS - 1) ] * P = [ 2*s - (2^COMB_BITS - 1) ] * P
1. 将盲化与梳状算法结合
最直接的想法是在计算(k - b)*G时,让其等于comb(s, G),即有:
(k - b) * G = comb(s, G) = [ 2*s - (2^COMB_BITS - 1) ] * G
由此可知只要解出相应s,即可通过调用(1)公式计算出(k-b)*G,s可以通过以下公式进行求解:
s = (k - b + (2^COMB_BITS - 1)) / 2 (mod order) (2)
这个公式需要对2进行模逆运算(相当于除法),在模运算中,除法是复杂且耗时的操作,需要避免。
2. 避免模除2
为了避免昂贵的模除2操作,这里采用了一个巧妙地优化,将公式中基点G除于2,不再计算comb(s, G),而是计算comb(d, G/2),仍利用最一开始的公式,则有:
comb(d, G/2) = sum( (2*d[i] - 1) * 2^i * (G/2) ) (3) = [ 2*d - (2^COMB_BITS - 1) ] * (G/2) = [ d - (2^COMB_BITS - 1)/2 ] * G
现在,令comb(d, G/2) = (k - b) * G,则有:
(k - b) * G = [ d - (2^COMB_BITS - 1)/2 ] * G
得到:
k - b = d - (2^COMB_BITS - 1)/2
最终解出d:
d = k - b + (2^COMB_BITS - 1)/2 (mod order) (4)
这里(2^COMB_BITS - 1)/2 是一个常量,可以预先计算。现在,计算d只需要一次模加法和一次模减法,完全避免了模除运算。在后续的源码实现中定义偏移量scalar_offset=(2^COMB_BITS - 1)/2 - b (mod order),则有d=k+scalar_offset,最终kG=(k-b)*G+b*G=comb(d, G/2)+ge_offset。
3. 梳状含义
在梳状算法中会将标量k拆分成多个位段,每个位段称之为块(Block),每个块中又有T个齿(Teeth),齿与齿之间又有S个间距(Spacing)。以源码中典型取值为例:
#define COMB_BLOCKS 11 #define COMB_TEETH 6 #define COMB_SPACING 4
表明会将标量k分成11块,每个块有6个齿,齿间距为4,则每个Block中包含24bits数据,梳子每次可以选中两两间隔为4的6bits数据,在这样的结构下11个块可以包含264bits数据,完全覆盖256bits的标量k(标量k还需进行数据位填充)。

定义mask(b) = sum(2^((b*COMB_TEETH + t)*COMB_SPACING) for t=0..COMB_TEETH-1),则当b取值从0到COMB_BLOCKS-1时,有以下对应关系:
mask(0) = 2^0 + 2^4 + 2^8 + 2^12 + 2^16 + 2^20, mask(1) = 2^24 + 2^28 + 2^32 + 2^36 + 2^40 + 2^44, mask(2) = 2^48 + 2^52 + 2^56 + 2^60 + 2^64 + 2^68, ... mask(10) = 2^240 + 2^244 + 2^248 + 2^252 + 2^256 + 2^260
由此可通过这些掩码拆分比特位d[i],具体来说,每个掩码会被使用COMB_SPACING次,且每次使用时的偏移量不同。
d = (d & mask(0)<<0) + (d & mask(1)<<0) + ... + (d & mask(COMB_BLOCKS-1)<<0) + (d & mask(0)<<1) + (d & mask(1)<<1) + ... + (d & mask(COMB_BLOCKS-1)<<1) + ... (d & mask(0)<<(COMB_SPACING-1)) + ...
接下来定义:
table(b, m) = (m - mask(b)/2) * G (5)
这里b=0..COMB_BLOCKS-1,m=(d & mask(b)),m是标量d在b块中对应的值,每个块对应的m可以有2^COMB_TEETH个不同取值,可以预计算m对应的点乘值m*G。
table(b, m) = (m - mask(b)/2)*G = ((d&mask(b)) - mask(b)/2)*G = (2(d&mask(b)) - mask(b))*G/2 = ((2d - 1)&mask(b))*G/2 = sum(2^i * (2*d[i] - 1) * G/2) 这里i遍历掩码mask(b)中的置位比特位,即最终有:
table(b, m) = sum(2^i * (2*d[i] - 1) * G/2) (6)
例如当m=2^48 + 2^56 + 2^68时(位于块2中的值),则有table(2, m) = (2^48 - 2^52 + 2^56 - 2^60 - 2^64 + 2^68) * G/2。
结合以上定义,可以重写comb(d, G/2):
comb(d, G/2) = 2^0 * (table(0, d>>0 & mask(0)) + ... + table(COMB_BLOCKS-1, d>>0 & mask(COMP_BLOCKS-1))) (7) + 2^1 * (table(0, d>>1 & mask(0)) + ... + table(COMB_BLOCKS-1, d>>1 & mask(COMP_BLOCKS-1))) + 2^2 * (table(0, d>>2 & mask(0)) + ... + table(COMB_BLOCKS-1, d>>2 & mask(COMP_BLOCKS-1))) + ... + 2^(COMB_SPACING-1) * (table(0, d>>(COMB_SPACING-1) & mask(0)) + ...)
即:
sum(2^i * sum(table(b, d>>i & mask(b)), b=0..COMB_BLOCKS-1), i=0..COMB_SPACING-1)
以下是计算过程伪代码:
c = infinity for comb_off in range(COMB_SPACING - 1, -1, -1): for block in range(COMB_BLOCKS): c += table(block, (d >> comb_off) & mask(block)) if comb_off > 0: c = 2*c return c
在以上伪代码中,梳子是从高位“梳到”低位的,即依次先处理每个块的高位,再依次处理每个块的低位。
4. 折半表
之前已经有结论每个块对应的m可以有2^COMB_TEETH个不同取值,所以对于table(b, m)来说需要有2^COMB_TEETH个表项才能覆盖该b块所有可能取值,但实际上只需一半的表项即可覆盖所有可能取值,即table(b, m)实际只包含2^(COMB_TEETH-1)个表项,以下是分析过程:
由m=(d & mask(b)),令m'是m所有位反转对应的值,则有m'=m XOR mask(b),进而有table(b, m') = table(b, m XOR mask(b)) = table(b, mask(b) - m) = (mask(b) - m - mask(b)/2)*G = -(m - mask(b)/2)*G = -table(b, m)。
即如果m'对应是m的所有位反转,那么m'对应的table表项即为m相应表项的负值,对于任意椭圆点P = (x, y),其负值很容易求得即-P = (x, -y),所以table(b, m)表只需保存一半的表项,另一半的位反转表项,只需对相应的表项取负即可。对于0块来说,当梳齿对应块中最低位时,有以下对应关系:

例如由m=2^0 + 2^8 + 2^16时的表项(对应点P=(x, y)),可以直接求出m'=2^4 + 2^12 + 2^20的表项(对应点-P = (x, -y)),只需要对m值对应的表项中y值取负即可得到m'值对应的表项。
2 源码详解
2.1 预计算表
函数secp256k1_ecmult_gen_compute_table用于产生第1节中的table(b, m)表项,函数源码如下:
1 static void secp256k1_ecmult_gen_compute_table(secp256k1_ge_storage* table, const secp256k1_ge* gen, int blocks, int teeth, int spacing) { 2 size_t points = ((size_t)1) << (teeth - 1); // 每个块的预计算点数 = 2^(teeth-1) 3 size_t points_total = points * blocks; // 总共预计算的点数 = 每个块的预计算点数 * 块数 4 secp256k1_ge* prec = checked_malloc(&default_error_callback, points_total * sizeof(*prec)); // 长度为总预计算点数的仿射点数组 5 secp256k1_gej* ds = checked_malloc(&default_error_callback, teeth * sizeof(*ds)); // 每块的“tooth"的雅可比坐标点数组 6 secp256k1_gej* vs = checked_malloc(&default_error_callback, points_total * sizeof(*vs)); // 长度为总预计算点数的雅可比坐标点数组 7 secp256k1_gej u; 8 size_t vs_pos = 0; 9 secp256k1_scalar half; 10 secp256k1_ge halfgenAffine; 11 secp256k1_ge_storage halfgenStorage; 12 int block, i; 13 14 VERIFY_CHECK(points_total > 0); 15 16 /* u is the running power of two times gen we're working with, initially gen/2. */ 17 secp256k1_scalar_half(&half, &secp256k1_scalar_one); 18 //print_scalar(&half, "0x", "\n"); 19 secp256k1_gej_set_infinity(&u); 20 for (i = 255; i >= 0; --i) { 21 /* Use a very simple multiplication ladder to avoid dependency on ecmult. */ 22 secp256k1_gej_double_var(&u, &u, NULL); 23 if (secp256k1_scalar_get_bits_limb32(&half, i, 1)) { 24 secp256k1_gej_add_ge_var(&u, &u, gen, NULL); 25 } 26 } 27 28 secp256k1_ge_set_gej(&halfgenAffine, &u); 29 secp256k1_ge_to_storage(&halfgenStorage, &halfgenAffine); 30 //print_storage(&halfgenStorage.x, "0x", "\n"); 31 //print_storage(&halfgenStorage.y, "0x", "\n"); 32 #ifdef VERIFY 33 { 34 /* Verify that u*2 = gen. */ 35 secp256k1_gej double_u; 36 secp256k1_gej_double_var(&double_u, &u, NULL); 37 VERIFY_CHECK(secp256k1_gej_eq_ge_var(&double_u, gen)); 38 } 39 #endif 40 41 for (block = 0; block < blocks; ++block) { 42 int tooth; 43 /* Here u = 2^(block*teeth*spacing) * gen/2. */ 44 secp256k1_gej sum; 45 secp256k1_gej_set_infinity(&sum); 46 for (tooth = 0; tooth < teeth; ++tooth) { 47 /* Here u = 2^((block*teeth + tooth)*spacing) * gen/2. */ 48 /* Make sum = sum(2^((block*teeth + t)*spacing), t=0..tooth) * gen/2. */ 49 secp256k1_gej_add_var(&sum, &sum, &u, NULL); 50 /* Make u = 2^((block*teeth + tooth)*spacing + 1) * gen/2. */ 51 secp256k1_gej_double_var(&u, &u, NULL); 52 /* Make ds[tooth] = u = 2^((block*teeth + tooth)*spacing + 1) * gen/2. */ 53 ds[tooth] = u; 54 /* Make u = 2^((block*teeth + tooth + 1)*spacing) * gen/2, unless at the end. */ 55 if (block + tooth != blocks + teeth - 2) { 56 int bit_off; 57 for (bit_off = 1; bit_off < spacing; ++bit_off) { 58 secp256k1_gej_double_var(&u, &u, NULL); 59 } 60 } 61 } 62 /* Now u = 2^((block*teeth + teeth)*spacing) * gen/2 63 * = 2^((block+1)*teeth*spacing) * gen/2 */ 64 65 /* Next, compute the table entries for block number block in Jacobian coordinates. 66 * The entries will occupy vs[block*points + i] for i=0..points-1. 67 * We start by computing the first (i=0) value corresponding to all summed 68 * powers of two times G being negative. */ 69 secp256k1_gej_neg(&vs[vs_pos++], &sum); 70 /*secp256k1_ge_set_gej(&halfgenAffine, &vs[vs_pos - 1]); 71 secp256k1_ge_to_storage(&halfgenStorage, &halfgenAffine); 72 print_storage(&halfgenStorage.x, "0x", "\n"); 73 print_storage(&halfgenStorage.y, "0x", "\n");*/ 74 /* And then teeth-1 times "double" the range of i values for which the table 75 * is computed: in each iteration, double the table by taking an existing 76 * table entry and adding ds[tooth]. */ 77 for (tooth = 0; tooth < teeth - 1; ++tooth) { 78 size_t stride = ((size_t)1) << tooth; 79 size_t index; 80 for (index = 0; index < stride; ++index, ++vs_pos) { 81 secp256k1_gej_add_var(&vs[vs_pos], &vs[vs_pos - stride], &ds[tooth], NULL); 82 } 83 } 84 } 85 VERIFY_CHECK(vs_pos == points_total); 86 87 /* Convert all points simultaneously from secp256k1_gej to secp256k1_ge. */ 88 secp256k1_ge_set_all_gej_var(prec, vs, points_total); 89 /* Convert all points from secp256k1_ge to secp256k1_ge_storage output. */ 90 for (block = 0; block < blocks; ++block) { 91 size_t index; 92 for (index = 0; index < points; ++index) { 93 VERIFY_CHECK(!secp256k1_ge_is_infinity(&prec[block * points + index])); 94 secp256k1_ge_to_storage(&table[block * points + index], &prec[block * points + index]); 95 print_storage(&table[block * points + index].x, "0x", "\n"); 96 print_storage(&table[block * points + index].y, "0x", "\n"); 97 } 98 } 99 100 /* Free memory. */ 101 free(vs); 102 free(ds); 103 free(prec); 104 }
正如之前分析代码中第2行给出了每个块儿需要进行预计算点的个数(即table(b, m)在固定b时的表项数),COMB_TEETH=6时,表项数是2^5=32个;第3行为b取值从0到COMB_BLOCKS-1时完整表中点的总数,以COMB_BLOCKS=11为例,点的总数是32*11=352;接下来第4~6行为对应的表项分配内存空间,其中ds用于存储在每个块中梳齿对应的“权重”,所以其大小是梳齿个数6,以0块儿为例,其取值为2*G/2,2*2^4*G/2,2*2^8*G/2,2*2^12*G/2,2*2^16*G/2,2*2^20*G/2,后续给出详细求解过程;第17~26行先求得标量1/2 mod order,再用通用的倍点加法求射影点u=G/2;第28,29行分别获取点u对应的仿射坐标及存储坐标值;第33~38行验证部分是检查2*u是否等于生成点G。
接下来,第11行处的for循环用于对11个块儿,依次求块对应的table(b, m)内容;之后第44,45行定义临时变量sum,并将其初始化为零点,第46行的for循环用于求之前所说的ds,以及公式(6)中减数部分的累加和sum;具体来说,第47,48行给出了后续u和sum的具体计算公式;接下来第49行将上轮更新过的u加到sum上(两个for循环都为第一次时,u值为G/2,加完以后sum=G/2);之后第51行将u翻倍,例如在tooth=0时,u=2*G/2;第53~60行,先将u赋值给ds[tooth],然后再将u翻SPACING-1倍,算上第51行翻倍u相当于共翻倍SPACING次(当SPACING=4时对应2^4),另外55行的if判断用于在最后一个块最后一次时,由于不再使用这时已无需对u再进行SPACING-1次翻倍操作,for循环完毕已经依次求出之前所说的梳齿“权重”——ds,以及公式(6)中减数部分的累加和——sum。
第69行将累加和取负(因为sum对应公式中的减数部分)后,赋值给当前块中的第一个表项vs[pos],对应所有梳齿位都位0时表项值,接下来,第77行for循环分别计算梳齿0,1,...,teeth-2齿位对应是1时的table的表项值;第78行用于计算对应梳齿位为1时表项的个数,如第0个梳齿位为1时,只能产生2^0=1个表项000001,第1个梳齿位为1时,可以产生2^1=2个表项000010和000011,第2个梳齿位为1时,可以产生2^2=4个表项000100,000101,000110,000111,依次类推第teeth-2=4齿位对应是1时,可以产生2^4=16个表项;之后第80~82行的for循环依次产生之前折半表部分图中前半部分对应的表项值,总个数是1+1+2+4+..+16=32。
代码接下来的内容主要是坐标转换相关内容,这里不再进行详细解释,总之循环执行完毕会产生所有11个块对用的查找表。
2.2 计算k*G
接下来需要看如何利用上一小节产生的查找表进行k*G计算,仍旧先给出计算函数secp256k1_ecmult_gen源码:
1 static void secp256k1_ecmult_gen(const secp256k1_ecmult_gen_context *ctx, secp256k1_gej *r, const secp256k1_scalar *gn) { 2 uint32_t comb_off; 3 secp256k1_ge add; 4 secp256k1_fe neg; 5 secp256k1_ge_storage adds; 6 secp256k1_scalar d; 7 /* Array of uint32_t values large enough to store COMB_BITS bits. Only the bottom 8 * 8 are ever nonzero, but having the zero padding at the end if COMB_BITS>256 9 * avoids the need to deal with out-of-bounds reads from a scalar. */ 10 uint32_t recoded[(COMB_BITS + 31) >> 5] = {0}; 11 int first = 1, i; 12 13 memset(&adds, 0, sizeof(adds)); 14 15 /* We want to compute R = gn*G. 16 * 17 * To blind the scalar used in the computation, we rewrite this to be 18 * R = (gn - b)*G + b*G, with a blinding value b determined by the context. 19 * 20 * The multiplication (gn-b)*G will be performed using a signed-digit multi-comb (see Section 21 * 3.3 of "Fast and compact elliptic-curve cryptography" by Mike Hamburg, 22 * https://eprint.iacr.org/2012/309). 23 * 24 * Let comb(s, P) = sum((2*s[i]-1)*2^i*P for i=0..COMB_BITS-1), where s[i] is the i'th bit of 25 * the binary representation of scalar s. So the s[i] values determine whether -2^i*P (s[i]=0) 26 * or +2^i*P (s[i]=1) are added together. COMB_BITS is at least 256, so all bits of s are 27 * covered. By manipulating: 28 * 29 * comb(s, P) = sum((2*s[i]-1)*2^i*P for i=0..COMB_BITS-1) 30 * <=> comb(s, P) = sum((2*s[i]-1)*2^i for i=0..COMB_BITS-1) * P 31 * <=> comb(s, P) = (2*sum(s[i]*2^i for i=0..COMB_BITS-1) - sum(2^i for i=0..COMB_BITS-1)) * P 32 * <=> comb(s, P) = (2*s - (2^COMB_BITS - 1)) * P 33 * 34 * If we wanted to compute (gn-b)*G as comb(s, G), it would need to hold that 35 * 36 * (gn - b) * G = (2*s - (2^COMB_BITS - 1)) * G 37 * <=> s = (gn - b + (2^COMB_BITS - 1))/2 (mod order) 38 * 39 * We use an alternative here that avoids the modular division by two: instead we compute 40 * (gn-b)*G as comb(d, G/2). For that to hold it must be the case that 41 * 42 * (gn - b) * G = (2*d - (2^COMB_BITS - 1)) * (G/2) 43 * <=> d = gn - b + (2^COMB_BITS - 1)/2 (mod order) 44 * 45 * Adding precomputation, our final equations become: 46 * 47 * ctx->scalar_offset = (2^COMB_BITS - 1)/2 - b (mod order) 48 * ctx->ge_offset = b*G 49 * d = gn + ctx->scalar_offset (mod order) 50 * R = comb(d, G/2) + ctx->ge_offset 51 * 52 * comb(d, G/2) function is then computed by summing + or - 2^(i-1)*G, for i=0..COMB_BITS-1, 53 * depending on the value of the bits d[i] of the binary representation of scalar d. 54 */ 55 56 /* Compute the scalar d = (gn + ctx->scalar_offset). */ 57 secp256k1_scalar_add(&d, &ctx->scalar_offset, gn); 58 /* Convert to recoded array. */ 59 for (i = 0; i < 8 && i < ((COMB_BITS + 31) >> 5); ++i) { 60 recoded[i] = secp256k1_scalar_get_bits_limb32(&d, 32 * i, 32); 61 } 62 secp256k1_scalar_clear(&d); 63 64 /* In secp256k1_ecmult_gen_prec_table we have precomputed sums of the 65 * (2*d[i]-1) * 2^(i-1) * G points, for various combinations of i positions. 66 * We rewrite our equation in terms of these table entries. 67 * 68 * Let mask(b) = sum(2^((b*COMB_TEETH + t)*COMB_SPACING) for t=0..COMB_TEETH-1), 69 * with b ranging from 0 to COMB_BLOCKS-1. So for example with COMB_BLOCKS=11, 70 * COMB_TEETH=6, COMB_SPACING=4, we would have: 71 * mask(0) = 2^0 + 2^4 + 2^8 + 2^12 + 2^16 + 2^20, 72 * mask(1) = 2^24 + 2^28 + 2^32 + 2^36 + 2^40 + 2^44, 73 * mask(2) = 2^48 + 2^52 + 2^56 + 2^60 + 2^64 + 2^68, 74 * ... 75 * mask(10) = 2^240 + 2^244 + 2^248 + 2^252 + 2^256 + 2^260 76 * 77 * We will split up the bits d[i] using these masks. Specifically, each mask is 78 * used COMB_SPACING times, with different shifts: 79 * 80 * d = (d & mask(0)<<0) + (d & mask(1)<<0) + ... + (d & mask(COMB_BLOCKS-1)<<0) + 81 * (d & mask(0)<<1) + (d & mask(1)<<1) + ... + (d & mask(COMB_BLOCKS-1)<<1) + 82 * ... 83 * (d & mask(0)<<(COMB_SPACING-1)) + ... 84 * 85 * Now define table(b, m) = (m - mask(b)/2) * G, and we will precompute these values for 86 * b=0..COMB_BLOCKS-1, and for all values m which (d & mask(b)) can take (so m can take on 87 * 2^COMB_TEETH distinct values). 88 * 89 * If m=(d & mask(b)), then table(b, m) is the sum of 2^i * (2*d[i]-1) * G/2, with i 90 * iterating over the set bits in mask(b). In our example, table(2, 2^48 + 2^56 + 2^68) 91 * would equal (2^48 - 2^52 + 2^56 - 2^60 - 2^64 + 2^68) * G/2. 92 * 93 * With that, we can rewrite comb(d, G/2) as: 94 * 95 * 2^0 * (table(0, d>>0 & mask(0)) + ... + table(COMB_BLOCKS-1, d>>0 & mask(COMP_BLOCKS-1))) 96 * + 2^1 * (table(0, d>>1 & mask(0)) + ... + table(COMB_BLOCKS-1, d>>1 & mask(COMP_BLOCKS-1))) 97 * + 2^2 * (table(0, d>>2 & mask(0)) + ... + table(COMB_BLOCKS-1, d>>2 & mask(COMP_BLOCKS-1))) 98 * + ... 99 * + 2^(COMB_SPACING-1) * (table(0, d>>(COMB_SPACING-1) & mask(0)) + ...) 100 * 101 * Or more generically as 102 * 103 * sum(2^i * sum(table(b, d>>i & mask(b)), b=0..COMB_BLOCKS-1), i=0..COMB_SPACING-1) 104 * 105 * This is implemented using an outer loop that runs in reverse order over the lines of this 106 * equation, which in each iteration runs an inner loop that adds the terms of that line and 107 * then doubles the result before proceeding to the next line. 108 * 109 * In pseudocode: 110 * c = infinity 111 * for comb_off in range(COMB_SPACING - 1, -1, -1): 112 * for block in range(COMB_BLOCKS): 113 * c += table(block, (d >> comb_off) & mask(block)) 114 * if comb_off > 0: 115 * c = 2*c 116 * return c 117 * 118 * This computes c = comb(d, G/2), and thus finally R = c + ctx->ge_offset. Note that it would 119 * be possible to apply an initial offset instead of a final offset (moving ge_offset to take 120 * the place of infinity above), but the chosen approach allows using (in a future improvement) 121 * an incomplete addition formula for most of the multiplication. 122 * 123 * The last question is how to implement the table(b, m) function. For any value of b, 124 * m=(d & mask(b)) can only take on at most 2^COMB_TEETH possible values (the last one may have 125 * fewer as there mask(b) may exceed the curve order). So we could create COMB_BLOCK tables 126 * which contain a value for each such m value. 127 * 128 * Now note that if m=(d & mask(b)), then flipping the relevant bits of m results in negating 129 * the result of table(b, m). This is because table(b,m XOR mask(b)) = table(b, mask(b) - m) = 130 * (mask(b) - m - mask(b)/2)*G = (-m + mask(b)/2)*G = -(m - mask(b)/2)*G = -table(b, m). 131 * Because of this it suffices to only store the first half of the m values for every b. If an 132 * entry from the second half is needed, we look up its bit-flipped version instead, and negate 133 * it. 134 * 135 * secp256k1_ecmult_gen_prec_table[b][index] stores the table(b, m) entries. Index 136 * is the relevant mask(b) bits of m packed together without gaps. */ 137 138 /* Outer loop: iterate over comb_off from COMB_SPACING - 1 down to 0. */ 139 comb_off = COMB_SPACING - 1; 140 while (1) { 141 uint32_t block; 142 uint32_t bit_pos = comb_off; 143 /* Inner loop: for each block, add table entries to the result. */ 144 for (block = 0; block < COMB_BLOCKS; ++block) { 145 /* Gather the mask(block)-selected bits of d into bits. They're packed: 146 * bits[tooth] = d[(block*COMB_TEETH + tooth)*COMB_SPACING + comb_off]. */ 147 uint32_t bits = 0, sign, abs, index, tooth; 148 /* Instead of reading individual bits here to construct the bits variable, 149 * build up the result by xoring rotated reads together. In every iteration, 150 * one additional bit is made correct, starting at the bottom. The bits 151 * above that contain junk. This reduces leakage by avoiding computations 152 * on variables that can have only a low number of possible values (e.g., 153 * just two values when reading a single bit into a variable.) See: 154 * https://www.usenix.org/system/files/conference/usenixsecurity18/sec18-alam.pdf 155 */ 156 for (tooth = 0; tooth < COMB_TEETH; ++tooth) { 157 /* Construct bitdata s.t. the bottom bit is the bit we'd like to read. 158 * 159 * We could just set bitdata = recoded[bit_pos >> 5] >> (bit_pos & 0x1f) 160 * but this would simply discard the bits that fall off at the bottom, 161 * and thus, for example, bitdata could still have only two values if we 162 * happen to shift by exactly 31 positions. We use a rotation instead, 163 * which ensures that bitdata doesn't lose entropy. This relies on the 164 * rotation being atomic, i.e., the compiler emitting an actual rot 165 * instruction. */ 166 uint32_t bitdata = secp256k1_rotr32(recoded[bit_pos >> 5], bit_pos & 0x1f); 167 168 /* Clear the bit at position tooth, but sssh, don't tell clang. */ 169 uint32_t volatile vmask = ~(1 << tooth); 170 bits &= vmask; 171 172 /* Write the bit into position tooth (and junk into higher bits). */ 173 bits ^= bitdata << tooth; 174 bit_pos += COMB_SPACING; 175 } 176 177 /* If the top bit of bits is 1, flip them all (corresponding to looking up 178 * the negated table value), and remember to negate the result in sign. */ 179 sign = (bits >> (COMB_TEETH - 1)) & 1; 180 abs = (bits ^ -sign) & (COMB_POINTS - 1); 181 VERIFY_CHECK(sign == 0 || sign == 1); 182 VERIFY_CHECK(abs < COMB_POINTS); 183 184 /** This uses a conditional move to avoid any secret data in array indexes. 185 * _Any_ use of secret indexes has been demonstrated to result in timing 186 * sidechannels, even when the cache-line access patterns are uniform. 187 * See also: 188 * "A word of warning", CHES 2013 Rump Session, by Daniel J. Bernstein and Peter Schwabe 189 * (https://cryptojedi.org/peter/data/chesrump-20130822.pdf) and 190 * "Cache Attacks and Countermeasures: the Case of AES", RSA 2006, 191 * by Dag Arne Osvik, Adi Shamir, and Eran Tromer 192 * (https://eprint.iacr.org/2005/271.pdf) 193 */ 194 for (index = 0; index < COMB_POINTS; ++index) { 195 secp256k1_ge_storage_cmov(&adds, &secp256k1_ecmult_gen_prec_table[block][index], index == abs); 196 } 197 198 /* Set add=adds or add=-adds, in constant time, based on sign. */ 199 secp256k1_ge_from_storage(&add, &adds); 200 secp256k1_fe_negate(&neg, &add.y, 1); 201 secp256k1_fe_cmov(&add.y, &neg, sign); 202 203 /* Add the looked up and conditionally negated value to r. */ 204 if (EXPECT(first, 0)) { 205 /* If this is the first table lookup, we can skip addition. */ 206 secp256k1_gej_set_ge(r, &add); 207 /* Give the entry a random Z coordinate to blind intermediary results. */ 208 secp256k1_gej_rescale(r, &ctx->proj_blind); 209 first = 0; 210 } else { 211 secp256k1_gej_add_ge(r, r, &add); 212 } 213 } 214 215 /* Double the result, except in the last iteration. */ 216 if (comb_off-- == 0) break; 217 secp256k1_gej_double(r, r); 218 } 219 220 /* Correct for the scalar_offset added at the start (ge_offset = b*G, while b was 221 * subtracted from the input scalar gn). */ 222 secp256k1_gej_add_ge(r, r, &ctx->ge_offset); 223 224 /* Cleanup. */ 225 secp256k1_fe_clear(&neg); 226 secp256k1_ge_clear(&add); 227 secp256k1_memclear_explicit(&adds, sizeof(adds)); 228 secp256k1_memclear_explicit(&recoded, sizeof(recoded)); 229 }
源码第10给出一个位重编码变量recoded,用于存放标量gn(也即之前说的k)的二级制位,仍以之前的梳状结构为例,则COMB_BITS=11*6*4=264bits,则recoded长度为9,这时9*(1<<5)=288>264可以完全存储相应的重编码位;源码中的注释对应上一节的解析内容,接下来不再详细进行说明;第57行应用公式(4)对d进行求解;第59~62行从256bits的标量d中依次取出32bits并放入到recoded中,在32位实现下这里相当于把d中数据直接拷贝到recoded。
接下来是函数实现主体部分,首先第139行将comb_off初始化为COMB_SPACING-1,即从梳子从块儿的高位开始;之后140行处的while会依次处理comb_off位对应的各个梳齿取值,直到comb_off移动至0位;第142行将bit_pos初始化为com_off,梳齿对应第0块的高位;随后第144行用for循环依次处理COMB_BLOCKS个块儿;第156行使用for循环对于当前块儿的COMB_TEETH个梳齿位依次进行处理;第166行将包含bit_pos位的recoded[]进行循环右移,使得结果bitdata的最低位正好是我们需要的bit_pos位;第169行是tooth齿对应的掩码vmask,在掩码中tooth位为0其他位为1;第170行通过与掩码vmask做且操作清除目标位;接下来第173行将刚刚提取的位(bitdata最低位)写入到bits的第tooth个位置,bitdata<< tooth将包含所需位的32位数通过左移到将最低位移动到正确的位置——tooth,然后通过异或来将tooth值写入到bits(上一步已将bits的tooth位清零,零与其他值异或保留其他值);随后第174行将bit_pos移动到下一个梳齿位。可以看出循环结束后bits会在低COMB_TEETH位依次记录下当前块的梳齿位对应的值(bits低COMB_TEETH位以外值为无效数据),即将块儿中相应值“梳”出来。
之后,第179行将“梳”出来的bits最高位做为符号位;第180行取得除符号外,其他位实际应该的取值abs,其中-sign为mask,sign=0时,对应mask=0x00000000,sign=1时,对应mask=0xFFFFFFFF,即sign=0时取bits值(与0异或取原址),sign=1时bits值每个位都取反(与1异或取反值),之后通过&(COMB_POINT-1)获取bits mask后的低5bit值;第194~196行处的for循环取值abs对应的table表项值;第199~201行根据符号位确定是否进行取负操作;第204~212行根据是否为第一次将相应的表项值赋值或者附加到r上,在第一次时还可以会用proj_blind对r初始值进行盲化操作:

由图中解释可知经过盲化操作后,点r'虽然各个坐标分量的取值都已经都已经改变,但是由射影坐标的定义可知,其实r'和r对应同样的仿射坐标,即它们表示同一个点。
当144行的for循环执行完毕,表示当前comb_off梳齿位对应的所有块儿已经处理完毕,接下来第216行将梳齿向低位移位继续进行下一个梳齿位对应块的处理,直到COMB_SPACING=4个梳齿位都处理完毕则跳出while循环;另外因为梳齿位是从高位到低位进行的,所以第217行对r进行了翻倍操作,这相当于公式(7)中每行内的移位操作。
整个while循环执行完毕后得到的值r=(gn - b)*G,最终gn*G=(gn - b)*G + b*G,所以在222行又在r上加上了ge_offset=b*G,最终得到gn*G,求解结束。
2.3 补充说明
从上面的分析可知分块数COMB_BLOCKS和梳齿数COMB_TEETH共同决定了查找表的大小,其中分块数对查找表是线性影响,而梳齿数对查找表是指数级影响(影响更大),所以在内存受限或者优先考虑内存时,需要对这两个参数的取值进行斟酌考虑。另外COMB_BLOCKS决定了查表访存次数和点加操作次数,而COMB_SPACING决定了倍点操作次数,在进行CUDA编程时都需要根据实际情况,斟酌确定相关参数的取值。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号