CSP - J理论（1）

CSP-J理论(1)

CSP-J理论合集跳转

目录

本目录中所有标题单击均可以快速跳转哦

一.排列组合与概率

$\ \ \ \ \ $1.排列

$\ \ \ \ \ $2.组合

$\ \ \ \ \ $3.概率

$\ \ \ \ \ $4.圆排列

$\ \ \ \ \ $5.多重集合的排列

$\ \ \ \ \ $6.错位排列

二.二进制

$\ \ \ \ \ $1.数据范围

$\ \ \ \ \ $2.原、补、反码

$\ \ \ \ \ $3.位运算

三.递归问题复杂度分析

$\ \ \ \ \ $1.T(n)=2T(n/2)+n

$\ \ \ \ \ $2.T(n)=2T(n/2)+n^2

$\ \ \ \ \ $3:T(n)=2T(n/2)+sqrt(n)

一、排列组合与概率

一:排列

排列:n个数的排法,从第1位到第n位,每一个位置有n-i-1种选择,最后把每个位置的选择数相乘,得到: \(n \times n-1 \times n-2 \times ...\times 2 \times 1\),(即n阶乘)。如果要在 n 个数里挑 m 个组 m 位数,数量就是$ n \times n-1 \times n-2 \times n-3 \times ... \times n-m+1$,即A(n,m)

二:组合

组合:n个数的选法。

组合和排列的区别在于排列看来,（1,2）和（2,1）是两种排列,但在组合看来,（1,2）和（2,1）是一种组合。

所以,组合就是在排列的基础上再/m,比如在n个数里选m个,就是\(n \times n-1 \times n-2 \times n-3 \times ...\times n-m+1\)再\(/m\),即C（n,m）,但是如果我们在n-m+1后面补上一个从n-m乘到1的表达式,那么就变成了n!,但是也要再除以（n-m）!,因为上面乘了（n-m）!,下面也乘（n-m）!,结果不变。

组合数常见结论:C（n,0）=1,C（n,1）=n,C（n,n）=1,C（n,m）=C（n,n-m）。

三:概率

概率:就是选择物品数量/总数,如probability这个字符串里取字符,取到字符b的概率就是2/字符串的长度11。

四:圆排列

圆排列就是将几个数围成一圈的排列。

如下面这个排列

就是一个圆排列。

圆排列的特点是将圆旋转，仍然是同一个圆排列，如

和

都是同一个圆排列

圆排列的排列数是(n-1)!

五:多重集合的排列

多重集合是指如{1,1,2,3,3}这样的集合。假设这个集合里有n种数，每个数都有无限个，要选出k个，排列数就是\(n^k\)。

但如果每种数的数量固定，设第一种数的数目为\(a_1\)、第二种为\(a_2\)...那么排列数就是\(\frac{n!}{a_1!a_2!...a_k!}\)

六:错位排列

错位排列是指第i个位置不是i的排列，如{3,2,1}

错位排列的排列数是

\[ f(x) = \begin{cases} 0 & x = 1 \\ 1 & x = 2 \\ (i-1)*(f_{i-1}+f_{i-2}) & x>=3 \end{cases}\]

二、二进制

一:数据范围

int类型的数据范围是\(-2^{31}\to2^{31}-1\)

unsigned int类型的数据范围是\(0\to2^{32}-1\)

long long类型的数据范围是\(-2^{63}\to2^{63}-1\)

unsigned long long类型的数据范围是\(0\to2^{64}-1\)

二:原、补、反码

原码的第一位是符号位，用于表示正负，正为0，负为1，其他位就是这个数的二进制

反码是原码除符号位取反（0变1,1变0）

补码是反码+1

三:位运算

x<<y就是将x乘上\(2^y\)，x>>y就是将x除以\(2^y\)（向下取整）。

&：每一位都为1就是1

|：每一位有1就是1

^：每一位不同就为1，相同为0

~：对每一位进行取反（包括符号位）

lowbit：用于求得一个数二进制下最低位的1代表2的几次方。代码是x&-x

三、递归问题复杂度分析

一:T(n)=2T(n/2)+n

画出递归树

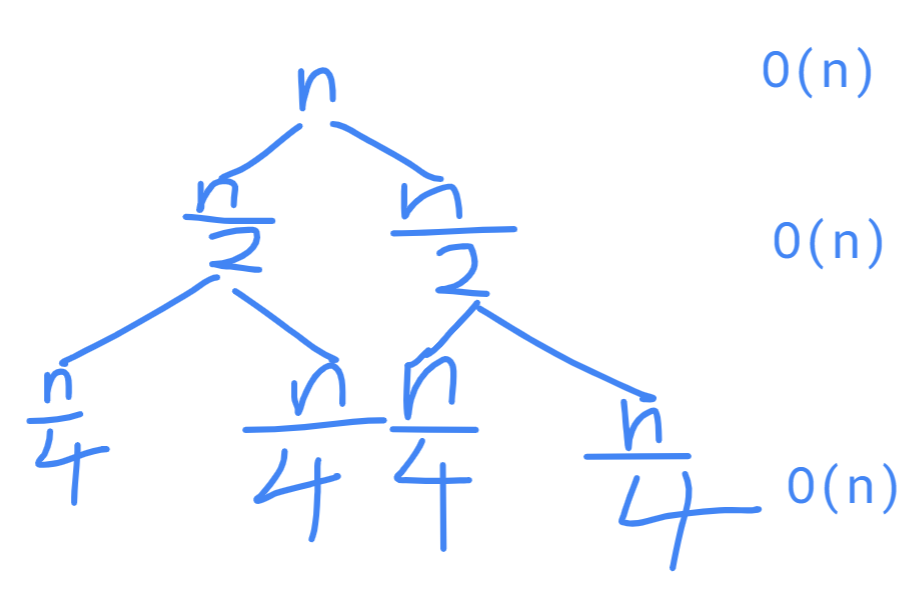
可以发现每一层都是O(n)，总复杂度为O(nlogn)。

二:T(n)=2T(n/2)+n^2

画出递归树

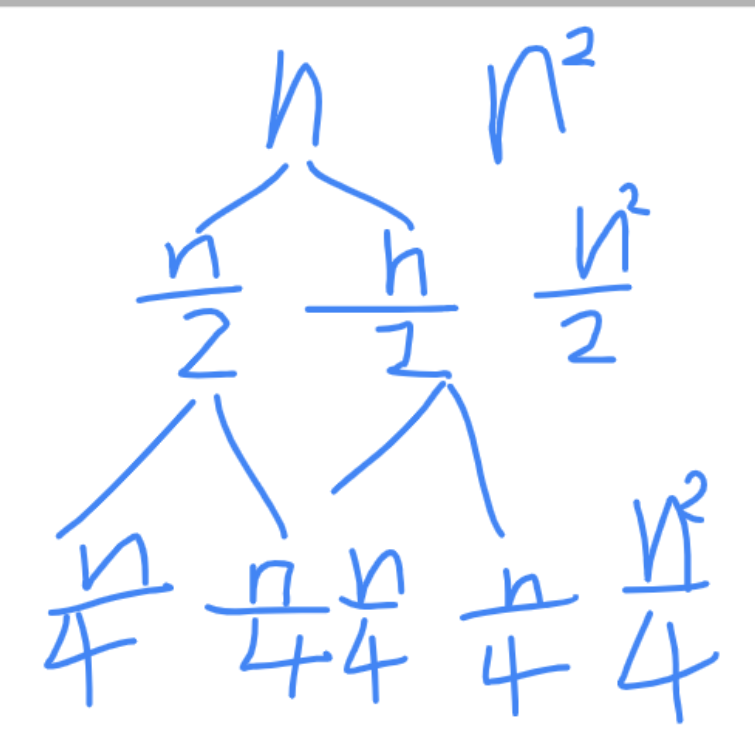
把每一层的加在一起，得到 \(n^2+\frac{n^2}{2}+\frac{n^2}{4}+...\)。

我们把 \(n^2\) 提取出来，得到 \(n^2 \times (1+\frac{1}{2}+\frac{1}{4}+...)\)。

我们可以发现右边的和无论如何都是小于 \(2\) 的，所以总复杂度为O(n^2)。

三:T(n)=2T(n/2)+sqrt(n)

画出递归树

求和可以得到是 \(\sqrt{n}+2\times\sqrt{\frac{n}{2}}+4\times\sqrt{\frac{n}{4}}+...\)。

我们把 \(\sqrt{n}\) 提取出来，可以得到 \(\sqrt{n}\times(1+\sqrt{2}+\sqrt{4}+...)\)。

利用等比数列求和公式，可以得到括号里是 \(\sqrt{n}\)，与前面的 \(\sqrt{n}\) 相乘，所以得到总复杂度为O(n)。