常见的六种排序算法实现
常见的六种排序算法实现
在写六种排序先写两个辅助的函数
交换数组的元素函数swap
/*辅助交换函数*/ int Swap(int* str, int pos1, int pos2) { if (str == NULL) { return -1; } if (pos1 < 0 || pos2 < 0) { return -2; } /*交换数组pos1的值和pos2的值*/ int temp = str[pos1]; str[pos1] = str[pos2]; str[pos2] = temp; return 0; } /*打印数组元素*/ void PrintArraryElement(int* str, int length) { assert(str != NULL); printf("\t\t\t"); for (int i = 0; i < length; i++) { printf("%d\t", str[i]); } printf("\n"); }
选择排序
/*选择排序*/ int SelectSort(int* str, int length) { /* 算法思想 第一次:i=0(j=1,此时比较str[0],str[1]。如果str[1]比str[0]还小的话,进行交换,此时str[0]是前2个最小值了。接着j=2的时候,也就是第3个元素的时候,在进行比较str[0],str[2]。如果str[2]比str[0]小的话,进行交换。此时str[0]就是前3个最小值了。类推。i=0;执行完的时候第一个元素str[0]一定是所有元素中最小的那一个。这样第一个元素就是有序的。 第二次:i=1执行过程和i=0类似,只是每次都是和str[1]进行比较了。str[0]是不参与比较的。所以i=1执行完后,str[1]一定是str[1]到str[length-1] 元素的最小值。这样前2个元素是有序的。 第三次:i=2。这样前3个元素是有序的。 第N次:i=n-1。 这样前N个元素是有序的。也就是所有元素都是有序的啦。 总结:每次都是和固定的位置那个元素进行比较。 */ assert(str != NULL); for (int i = 0; i < length; i++) { for (int j = i + 1; j < length; j++) { if (str[i] >str[j]) { Swap(str, i, j); } } } return 0; }
冒泡排序
/*冒泡排序*/ int BubbleSort(int* str, int length) { /* 算法思想 第一次:i=0(j=0,此时比较str[0],str[1]。如果str[1]比str[0]还小的话,进行交换,此时str[0]是前2个最小值了 str[1]是前2个最大值。接着j=1的时候,在进行比较str[1],str[2]。如果str[2]比str[1]小的话,进行交换。此时str[2]就是前3个最大值了。类推。i=0;执行完的时候最后一个元素str[length-1]一定是所有元素中最大的那一个。这样最后一个元素就是有序的。 第二次:i=1执行过程和i=0类似,每次相邻元素进行比较。所以i=1执行完后,倒数第二个元素str[length-2]一定是str[0]到str[length-2] 元素的最小值。这样后2个元素是有序的。 第三次:i=2。这样后3个元素是有序的。 第N次:i=n-1。 这样后N个元素是有序的。也就是所有元素都是有序的啦。 总结:每次都是相邻的元素进行比较,可以定义一个flag标示变量前面的结果是否有序进行优化。 */ assert(str != NULL); for (int i = 0; i < length; i++) { for (int j = 0; j < length - 1; j++) { if (str[j] > str[j + 1]) { Swap(str, j, j + 1); } } } return 0; }
插入排序
/*插入排序*/ int InsertSort(int* str, int length) { /* 算法思想 这里举例个数据 1 , 2 ,4 , 5 , 3 核心:就是取出来一个元素,然后和前面的有序序列进行比较,找到合适的位置。插进去,这个位置的后面的需要后移。 对于上面的这个数组一共5个元素,前4个是有序的。那么怎么讲第5个元素(3)插入到指定位置呢。 1.取出来: 先用一个变量pos 保存3这个元素的位置下标(pos =4),用一个value保存这个元素的值(3 )。 2.进行比较: 前面的4个元素(1,2,4,5)是有序的。先将 3和有序序列的最后一个元素(5)进行比较,3是小于5的,那么就将5这个元素放到原来3的为位置上去,这样5的这个位置就空出来了(也就是取出来了 pos =3)在和4进行比较。3小于4的。那么4这个元素后移下。这样pos=2的位置就空出来了。 3在和2进行比较,3是大于2的,for循环结束 把value(3) 赋值到pos位置上去,也就是str[pos] =value,级str[2] =3; 3.这样结果就是有效的了。 当然开始的时候前面几个不是有序的,至少第一个元素是有序的。那么就从第二个元素开始进行插入。也就是i=1开始,i=1结束的时候前面2个元素是有序 i=2,结束的时候前面3个元素是有序的。i=length -1,结束的时候前面length 个元素都是有序的。也就是整个数组是有序的。 */ assert(str != NULL); for (int i = 1; i < length; i++) { int pos = i; int value = str[i]; for (int j = i-1; j >=0 && str[j] >value; j--) { str[j + 1] = str[j]; pos = j; } str[pos] = value; } return 0; }
希尔排序
/*希尔排序*/ int ShellSort(int* str, int length) { /* 算法思想: 核心代码和插入排序一样。加入了分组处理,gap=gap/3+1 这样分组是效率最高的。 */ assert(str != NULL); int gap = length; do { gap = gap / 3 + 1; for (int i = gap; i < length; i+=gap) { int pos = i; int value = str[i]; for (int j = i - gap; j >= 0 && str[j] >value; j-=gap) { str[j + gap] = str[j]; pos = j; } str[pos] = value; } } while (gap > 1); return 0; }
快速排序
/*快速排序*/ /*******************************************************************************/ int Partition(int* str, int low, int high) { /* 函数功能:就是分隔str的low元素到high的元素(一共high-low+1个)比第一个元素(temp=str[low])大的都放到右边,比temp小的都放到左边。 算法思想: 这里给一个简单的数组来解释这个函数的功能 str 的数组元素(7个 low =0 high =6) 8,7,2,4,8,9,2 1.取temp =str[low]=8; 2;low就是第一个元素的下标,high就是最后一个元素的下标。第一次判断str[high] >= temp 为假,交换8和2 此时low =0 high =6数组变成了2,7,2,4,8,9,8 接着判断str[low]<=temp(2<8)为真,low++,此时low =1,high =6 ,接着判断str[low]<=temp(7<8)为真,low++,此时low=2,high=6,接着判断str[low]<=temp(2<8)为真low++,此时low=3,high=6 接着判断str[low]<=temp(4<8)为真low++,此时low=4,high=6,接着判断str[low]<=temp(8<=8)为真low++,low=5,high=6,接着判断str[low]<=temp(9<=8)为假,交换9和8,此时low=5,high=6 数组变成了2,7,2,4,8,8,9,接着进行判断str[high]>=temp(9>=8)为真,high--此时low=5,high=5 ,交换low和high位置元素,其实是一样的。最终返回一个low也就是5,也就是初始的第一个元素现在在这个数组的位置下标啦。最终得到的数组就是2,7,2,4,8,8,9. */ assert(str != NULL); int temp = str[low]; while (low <high) { while (low <high && str[high] >= temp) { high--; } Swap(str, low, high); while (low <high && str[low] <= temp) { low++; } Swap(str, low, high); } return low; } int QSort(int* str, int low, int high) { /* 算法思想: int par =Partition(str,low,high)执行后返回一个数组下标值par,str数组中数组下标小于par的元素都是小于str[par]的。数组下标大于par的元素都是大于str[par]的。这个时候str[par]就是不会在改变了。 QSort(str, low, par - 1);就是给low 到par-1的那些元素进行分割,每次都会确定一个str[par]的值不会再去改变的。 剩下的就是递归调用完成最终的排序计算。 */ assert(str != NULL); if (low < high) { int par = Partition(str, low, high); QSort(str, low, par - 1); QSort(str, par + 1, high); } return 0; } int QuickSort(int* str, int length) { assert(str != NULL); return QSort(str, 0, length - 1); }
归并排序
/*归并排序*/ /*******************************************************************************/ void Merge(int* src, int* dst, int low, int mid, int high) { /* 归并排序算法思想: src1 low到mid是有序的,mid到high是有序的。 这个函数就是将2个各自有序的数组合成一个数组 一个数组是1 ,4, 5 ,7 一个数组是2,3 ,6,8,9 10 第一次判断src[i] <src[j] 即1<2为真 dst[k++] =1;将1赋值到结果数组去i++,k++ 第二次判断src[i] <src[j}}即2<2为假 dst[k++] =2;将2赋值到结果数组去 j++,k++ 最终会有一个数组剩下元素,另一个数组没有元素的。 将那个数组的元素copy到结果数组中去。 */ assert(src != NULL); assert(dst != NULL); int i = low; int j = mid + 1; int k = low; while (i<=mid && j<=high) { /*每次插入两个数组的头部最小值到目标数组中,保证了目标数组是有序的*/ if (src[i] < src[j]) { dst[k++] = src[i++]; } else { dst[k++] = src[j++]; } } /*将剩下的那部分copy到目标数组中去*/ while (i<=mid) { dst[k++] = src[i++]; } while (j<=high) { dst[k++] = src[j++]; } } int MSort(int* src, int* dst, int low, int high, int max) { assert(src != NULL); assert(dst != NULL); if (low == high) { /*只有一个元素的时候直接给目标数组赋值了。不用在递归啦*/ dst[low] = src[low]; return 0; } else { int mid = (low + high) / 2; int *space = (int*)malloc(sizeof(int)* max); if (space == NULL) { return -1; } //递归调用进行分割直到只有一个元素递归结束 MSort(src, space, low, mid, max); MSort(src, space, mid + 1, high, max); //对递归的数据进行合并 Merge(space, dst, low, mid, high); if (space != NULL) { free(space); } return 0; } return 0; } int MergeSort(int* str,int length) { assert(str != NULL); return MSort(str, str, 0, length - 1, length); }
以上代码汇总
sort.h文件
#include <stdio.h> #include <stdlib.h> #include <string.h> #ifndef _SORT_H_ #define _SORT_H_ #ifdef __cplusplus extern "C" { #endif int __declspec(dllexport) SelectSort(int* str, int length); void __declspec(dllexport) PrintArraryElement(int* str, int length); int __declspec(dllexport) BubbleSort(int* str, int count); int __declspec(dllexport) InsertSort(int* str, int length); int __declspec(dllexport) ShellSort(int* str, int length); int __declspec(dllexport) QSort(int* str, int low, int high); int __declspec(dllexport) QuickSort(int* str, int length); int __declspec(dllexport) MergeSort(int* str, int length); #ifdef __cplusplus } #endif #endif
sort.cpp文件
#include <stdio.h> #include <stdlib.h> #include <string.h> #include "Sort.h" #include <assert.h> /*辅助交换函数*/ int Swap(int* str, int pos1, int pos2) { if (str == NULL) { return -1; } if (pos1 < 0 || pos2 < 0) { return -2; } /*交换数组pos1的值和pos2的值*/ int temp = str[pos1]; str[pos1] = str[pos2]; str[pos2] = temp; return 0; } /*打印数组元素*/ void PrintArraryElement(int* str, int length) { assert(str != NULL); printf("\t\t\t"); for (int i = 0; i < length; i++) { printf("%d\t", str[i]); } printf("\n"); } /*选择排序*/ int SelectSort(int* str, int length) { /* 算法思想 第一次:i=0(j=1,此时比较str[0],str[1]。如果str[1]比str[0]还小的话,进行交换,此时str[0]是前2个最小值了。接着j=2的时候,也就是第3个元素的时候,在进行比较str[0],str[2]。如果str[2]比str[0]小的话,进行交换。此时str[0]就是前3个最小值了。类推。i=0;执行完的时候第一个元素str[0]一定是所有元素中最小的那一个。这样第一个元素就是有序的。 第二次:i=1执行过程和i=0类似,只是每次都是和str[1]进行比较了。str[0]是不参与比较的。所以i=1执行完后,str[1]一定是str[1]到str[length-1] 元素的最小值。这样前2个元素是有序的。 第三次:i=2。这样前3个元素是有序的。 第N次:i=n-1。 这样前N个元素是有序的。也就是所有元素都是有序的啦。 总结:每次都是和固定的位置那个元素进行比较。 */ assert(str != NULL); for (int i = 0; i < length; i++) { for (int j = i + 1; j < length; j++) { if (str[i] >str[j]) { Swap(str, i, j); } } } return 0; } /*冒泡排序*/ int BubbleSort(int* str, int length) { /* 算法思想 第一次:i=0(j=0,此时比较str[0],str[1]。如果str[1]比str[0]还小的话,进行交换,此时str[0]是前2个最小值了 str[1]是前2个最大值。接着j=1的时候,在进行比较str[1],str[2]。如果str[2]比str[1]小的话,进行交换。此时str[2]就是前3个最大值了。类推。i=0;执行完的时候最后一个元素str[length-1]一定是所有元素中最大的那一个。这样最后一个元素就是有序的。 第二次:i=1执行过程和i=0类似,每次相邻元素进行比较。所以i=1执行完后,倒数第二个元素str[length-2]一定是str[0]到str[length-2] 元素的最小值。这样后2个元素是有序的。 第三次:i=2。这样后3个元素是有序的。 第N次:i=n-1。 这样后N个元素是有序的。也就是所有元素都是有序的啦。 总结:每次都是相邻的元素进行比较,可以定义一个flag标示变量前面的结果是否有序进行优化。 */ assert(str != NULL); for (int i = 0; i < length; i++) { for (int j = 0; j < length - 1; j++) { if (str[j] > str[j + 1]) { Swap(str, j, j + 1); } } } return 0; } /*插入排序*/ int InsertSort(int* str, int length) { /* 算法思想 这里举例个数据 1 , 2 ,4 , 5 , 3 核心:就是取出来一个元素,然后和前面的有序序列进行比较,找到合适的位置。插进去,这个位置的后面的需要后移。 对于上面的这个数组一共5个元素,前4个是有序的。那么怎么讲第5个元素(3)插入到指定位置呢。 1.取出来: 先用一个变量pos 保存3这个元素的位置下标(pos =4),用一个value保存这个元素的值(3 )。 2.进行比较: 前面的4个元素(1,2,4,5)是有序的。先将 3和有序序列的最后一个元素(5)进行比较,3是小于5的,那么就将5这个元素放到原来3的为位置上去,这样5的这个位置就空出来了(也就是取出来了 pos =3)在和4进行比较。3小于4的。那么4这个元素后移下。这样pos=2的位置就空出来了。 3在和2进行比较,3是大于2的,for循环结束 把value(3) 赋值到pos位置上去,也就是str[pos] =value,级str[2] =3; 3.这样结果就是有效的了。 当然开始的时候前面几个不是有序的,至少第一个元素是有序的。那么就从第二个元素开始进行插入。也就是i=1开始,i=1结束的时候前面2个元素是有序 i=2,结束的时候前面3个元素是有序的。i=length -1,结束的时候前面length 个元素都是有序的。也就是整个数组是有序的。 */ assert(str != NULL); for (int i = 1; i < length; i++) { int pos = i; int value = str[i]; for (int j = i-1; j >=0 && str[j] >value; j--) { str[j + 1] = str[j]; pos = j; } str[pos] = value; } return 0; } /*希尔排序*/ int ShellSort(int* str, int length) { /* 算法思想: 核心代码和插入排序一样。加入了分组处理,gap=gap/3+1 这样分组是效率最高的。 */ assert(str != NULL); int gap = length; do { gap = gap / 3 + 1; for (int i = gap; i < length; i+=gap) { int pos = i; int value = str[i]; for (int j = i - gap; j >= 0 && str[j] >value; j-=gap) { str[j + gap] = str[j]; pos = j; } str[pos] = value; } } while (gap > 1); return 0; } /*快速排序*/ /*******************************************************************************/ int Partition(int* str, int low, int high) { /* 函数功能:就是分隔str的low元素到high的元素(一共high-low+1个)比第一个元素(temp=str[low])大的都放到右边,比temp小的都放到左边。 算法思想: 这里给一个简单的数组来解释这个函数的功能 str 的数组元素(7个 low =0 high =6) 8,7,2,4,8,9,2 1.取temp =str[low]=8; 2;low就是第一个元素的下标,high就是最后一个元素的下标。第一次判断str[high] >= temp 为假,交换8和2 此时low =0 high =6数组变成了2,7,2,4,8,9,8 接着判断str[low]<=temp(2<8)为真,low++,此时low =1,high =6 ,接着判断str[low]<=temp(7<8)为真,low++,此时low=2,high=6,接着判断str[low]<=temp(2<8)为真low++,此时low=3,high=6 接着判断str[low]<=temp(4<8)为真low++,此时low=4,high=6,接着判断str[low]<=temp(8<=8)为真low++,low=5,high=6,接着判断str[low]<=temp(9<=8)为假,交换9和8,此时low=5,high=6 数组变成了2,7,2,4,8,8,9,接着进行判断str[high]>=temp(9>=8)为真,high--此时low=5,high=5 ,交换low和high位置元素,其实是一样的。最终返回一个low也就是5,也就是初始的第一个元素现在在这个数组的位置下标啦。最终得到的数组就是2,7,2,4,8,8,9. */ assert(str != NULL); int temp = str[low]; while (low <high) { while (low <high && str[high] >= temp) { high--; } Swap(str, low, high); while (low <high && str[low] <= temp) { low++; } Swap(str, low, high); } return low; } int QSort(int* str, int low, int high) { /* 算法思想: int par =Partition(str,low,high)执行后返回一个数组下标值par,str数组中数组下标小于par的元素都是小于str[par]的。数组下标大于par的元素都是大于str[par]的。这个时候str[par]就是不会在改变了。 QSort(str, low, par - 1);就是给low 到par-1的那些元素进行分割,每次都会确定一个str[par]的值不会再去改变的。 剩下的就是递归调用完成最终的排序计算。 */ assert(str != NULL); if (low < high) { int par = Partition(str, low, high); QSort(str, low, par - 1); QSort(str, par + 1, high); } return 0; } int QuickSort(int* str, int length) { assert(str != NULL); return QSort(str, 0, length - 1); } /*归并排序*/ /*******************************************************************************/ void Merge(int* src, int* dst, int low, int mid, int high) { /* 归并排序算法思想: src1 low到mid是有序的,mid到high是有序的。 这个函数就是将2个各自有序的数组合成一个数组 一个数组是1 ,4, 5 ,7 一个数组是2,3 ,6,8,9 10 第一次判断src[i] <src[j] 即1<2为真 dst[k++] =1;将1赋值到结果数组去i++,k++ 第二次判断src[i] <src[j}}即2<2为假 dst[k++] =2;将2赋值到结果数组去 j++,k++ 最终会有一个数组剩下元素,另一个数组没有元素的。 将那个数组的元素copy到结果数组中去。 */ assert(src != NULL); assert(dst != NULL); int i = low; int j = mid + 1; int k = low; while (i<=mid && j<=high) { /*每次插入两个数组的头部最小值到目标数组中,保证了目标数组是有序的*/ if (src[i] < src[j]) { dst[k++] = src[i++]; } else { dst[k++] = src[j++]; } } /*将剩下的那部分copy到目标数组中去*/ while (i<=mid) { dst[k++] = src[i++]; } while (j<=high) { dst[k++] = src[j++]; } } int MSort(int* src, int* dst, int low, int high, int max) { assert(src != NULL); assert(dst != NULL); if (low == high) { /*只有一个元素的时候直接给目标数组赋值了。不用在递归啦*/ dst[low] = src[low]; return 0; } else { int mid = (low + high) / 2; int *space = (int*)malloc(sizeof(int)* max); if (space == NULL) { return -1; } //递归调用进行分割直到只有一个元素递归结束 MSort(src, space, low, mid, max); MSort(src, space, mid + 1, high, max); //对递归的数据进行合并 Merge(space, dst, low, mid, high); if (space != NULL) { free(space); } return 0; } return 0; } int MergeSort(int* str,int length) { assert(str != NULL); return MSort(str, str, 0, length - 1, length); }
sortTest.cpp文件
#include <stdio.h> #include <stdlib.h> #include <string.h> #include "Sort.h" int main() { int str1[12] = { 12, 4, 53, 3, 2, 34, 6, 35, 1, 132, 324, 12 }; int str2[12] = { 12, 4, 53, 3, 2, 34, 6, 35, 1, 132, 324, 12 }; int str3[12] = { 12, 4, 53, 3, 2, 34, 6, 35, 1, 132, 324, 12 }; int str4[12] = { 12, 4, 53, 3, 2, 34, 6, 35, 1, 132, 324, 12 }; int str5[12] = { 12, 4, 53, 3, 2, 34, 6, 35, 1, 132, 324, 12 }; int str6[12] = { 12, 4, 53, 3, 2, 34, 6, 35, 1, 132, 324, 12 }; int str7[12] = { 12, 4, 53, 3, 2, 34, 6, 35, 1, 132, 324, 12 }; printf("打印排序前的原始结果:\n"); PrintArraryElement(str1, sizeof(str1) / sizeof(*str1)); /*选择排序*/ printf("执行选择排序的结果如下:\n"); SelectSort(str1, sizeof(str1) / sizeof(*str1)); PrintArraryElement(str1, sizeof(str1) / sizeof(*str1)); /*冒泡排序*/ printf("执行冒泡排序的结果如下:\n"); BubbleSort(str2, sizeof(str2) / sizeof(*str2)); PrintArraryElement(str2, sizeof(str2) / sizeof(*str2)); /*插入排序*/ printf("执行插入排序的结果如下:\n"); InsertSort(str3, sizeof(str3) / sizeof(*str3)); PrintArraryElement(str3, sizeof(str3) / sizeof(*str3)); /*希尔排序*/ printf("执行希尔排序的结果如下:\n"); ShellSort(str4, sizeof(str4) / sizeof(*str4)); PrintArraryElement(str4, sizeof(str4) / sizeof(*str4)); /*快速排序1*/ printf("执行快速排序1的结果如下:\n"); QuickSort(str5, sizeof(str5) / sizeof(*str5)); PrintArraryElement(str5, sizeof(str5) / sizeof(*str5)); /*快速排序2*/ printf("执行快速排序(只排序前6个)的结果如下:\n"); QSort(str6, 0,5 ); PrintArraryElement(str6, sizeof(str6) / sizeof(*str6)); /*归并排序*/ printf("执行归并排序的结果如下:\n"); MergeSort(str7, sizeof(str7) / sizeof(*str7)); PrintArraryElement(str7, sizeof(str7) / sizeof(*str7)); system("pause"); return 0; }
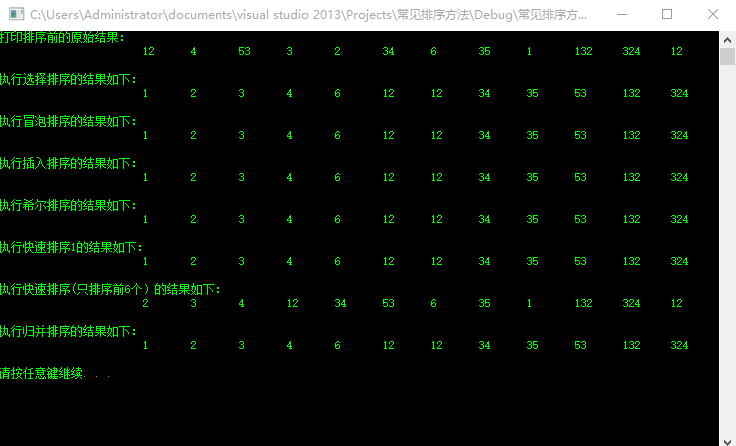
测试运行结果如下
posted on 2016-01-12 11:43 LinuxPanda 阅读(551) 评论(0) 收藏 举报

 浙公网安备 33010602011771号
浙公网安备 33010602011771号