力扣104题、559题、111题（二叉树的最大深度，n叉树的最大深度，二叉树的最小深度）

104、二叉树的最大深度

基本思想：

后序遍历

具体实现：

1.确定递归的参数和返回值：

参数：根节点

返回值：int类型，因为返回的是树的深度

2.确定终止条件

节点为空时，返回0,说明这个树的高度为0

3.单层递归的逻辑

先求左子树的深度，

再求右子树的深度，

最后求左右深度的最大的数值，然后+1（要算上当前的中间节点）

得到当前节点为根节点的树的深度

代码：

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth, rightDepth) + 1;

    }
}

 

 

基本思想：

前序遍历，回溯算法

 

代码：

class Solution {
    int result;
    public int maxDepth(TreeNode root) {
        result = 0;
        if (root == null) return result;
        result = getDepth(root, 1);
        return result;
    }
     public int getDepth(TreeNode node, int depth){
         result = depth > result ? depth:result;//前序遍历
         if (node.left == null && node.right == null) return result;
         if (node.left != null){//左子树
             depth++;//深度+1
             getDepth(node.left, depth);
             depth--;//回溯，深度-1
         }
         if (node.right != null){
             depth++;
             getDepth(node.right, depth);
             depth--;
         }
         return result;
     }
}

 

 

基本思想：

迭代法，层序遍历

具体实现：

一层一层遍历二叉树，记录遍历的层数就是二叉树的深度

代码：

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        int depth = 0;
        while(!deque.isEmpty()) {
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++){
                TreeNode poll = deque.poll();
                if (poll.left != null){
                    deque.offer(poll.left);
                }
                if (poll.right != null){
                    deque.offer(poll.right);
                }
            }
        }
        return depth;
     
    }
}

 

 

 

 

 

559、n叉树的最大深度

递归法

class Solution {
    public int maxDepth(Node root) {
        if (root == null) {//二叉树不存在，返回高度0
            return 0;
        } else if (root.children.isEmpty()) {//根节点没有孩子节点，返回高度1
            return 1;  
        } else {
            List<Integer> heights = new LinkedList<>();
            for (Node item : root.children) {//根节点有孩子节点
                heights.add(maxDepth(item)); //遍历每个孩子节点，求出以孩子节点为根的树的高度
            }
        return Collections.max(heights) + 1;
         }
    }
}

 

 

迭代法：

class Solution {
    public int maxDepth(Node root) {
        if (root == null) return 0;
        Deque<Node> deque = new LinkedList<>();
        deque.offer(root);
        int depth = 0;
        while(!deque.isEmpty()) {
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++){
                Node node = deque.poll();
                for (int j = 0; j < node.children.size();j++){
                    if (node.children.get(j) != null){
                        deque.offer(node.children.get(j));
                    }
                }
            }
        }
        return depth;
    }
}

 

class Solution {
    public int maxDepth(Node root) {
        if (root == null)   return 0;
        int depth = 0;
        Queue<Node> que = new LinkedList<>();
        que.offer(root);
        while (!que.isEmpty())
        {
            depth ++;
            int len = que.size();
            while (len > 0)
            {
                Node node = que.poll();
                 if (node.children != null){
                    for (Node child : node.children){
                        que.offer(child);
                    }
                 }
                len--;
            }
        }
        return depth;
    }
}

 

 

111、二叉树的最小深度

具体实现:

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

所以不能用104题后序遍历的套路

 

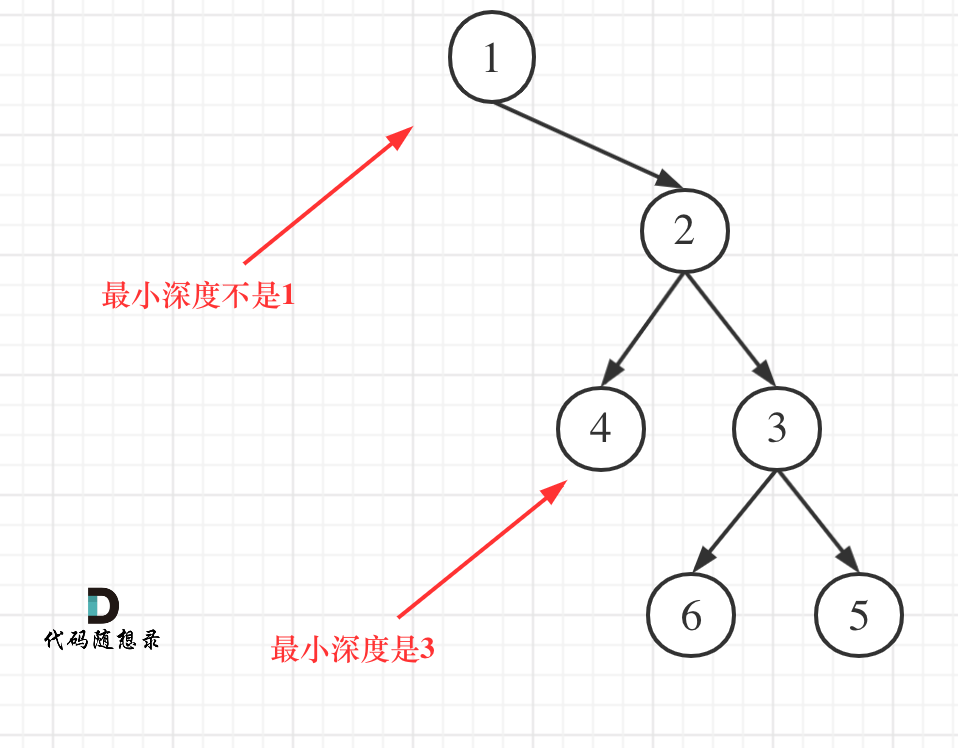
 左子树为空，右子树不为空，最小深度是1+左子树的深度

右子树为空，左子树不为空，最小深度是1+右子树的深度

左右子树都不为空，最小深度是左右子树深度最小值+1

代码：

class Solution {
    public int minDepth(TreeNode root) {
         if (root == null) {
            return 0;
        }
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);
        if (root.left == null && root.right != null) {
            return rightDepth + 1;
        }
        if (root.right == null && root.left != null) {
            return leftDepth + 1;
        }
        // 左右结点都不为null
        return Math.min(leftDepth, rightDepth) + 1;
    }
}

 

 

迭代法（层序遍历）

class Solution {
    public int minDepth(TreeNode root) {
         if (root == null) {
            return 0;
        }
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        int depth = 0;
        while (!deque.isEmpty()){
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++){
                TreeNode poll = deque.poll();
                if (poll.left == null && poll.right == null){
                    return depth;  // 是叶子结点，直接返回depth，因为从上往下遍历，所以该值就是最小值
                }
                if (poll.left != null){
                    deque.offer(poll.left);
                }
                if (poll.right != null){
                    deque.offer(poll.right);
                }
            }
        }
        return depth;
        
    }
}