E - Max Min AtCoder Beginner Contest 247

max min

We have a number sequence \(A = (A_1, A_2, \dots, A_N)\) of length \(N\) and integers \(X\) and \(Y\). Find the number of pairs of integers \((L, R)\) satisfying all the conditions below.

给定数列\(A = (A_1, A_2, \dots, A_N)\)，求有多少数对 \((L, R)\) 满足以下条件

• \(1 \leq L \leq R \leq N\)
• The maximum value of \(A_L, A_{L+1}, \dots, A_R\) is \(X\), and the minimum is \(Y\).（\(A_L, A_{L+1}, \dots, A_R\)中最大的是\(X\)，最小的是\(Y\)。）

Constraints

\(1≤N≤2×10^5\)

\(1 \leq A_i \leq 2 \times 10^5\)

\(1 \leq Y \leq X \leq 2 \times 10^5\)

All values in input are integers.

输入

N X Y
A1 A2 …… AN

输出

输出答案

题目解析

容斥原理

假设函数\(f(x,y)\)为所有值都在\((x,y)\)之内的区间的对数，那么我们可以通过容斥原理，得到上限为\(Y\)，下界为\(X\)的答案数量。

由于\((x,y)\)是个很大的范围，势必包括了不以\(Y\)为最大值，不以\(X\)为最小值的区间，因此我们需要减去这些区间。

显而易见，区间\((x+1,y)\)的下限一定不是\(X\)，区间\((x,y-1)\)的上限是\(y-1\)，一定不是\(Y\)，所有需要减去这两个区间。

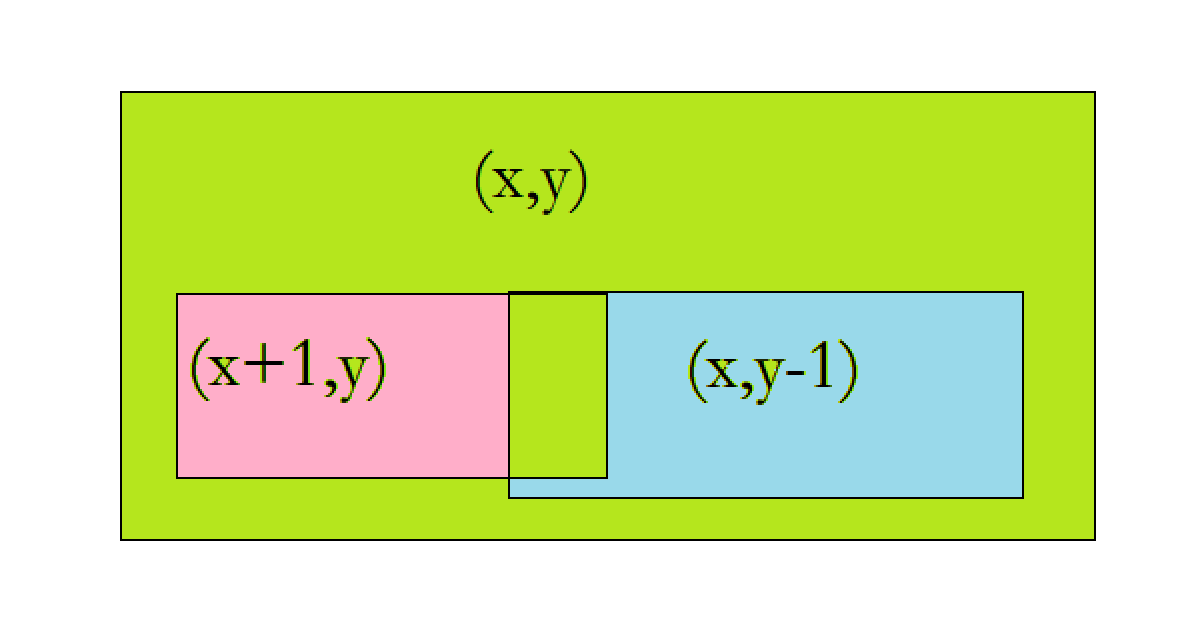
值得注意的是，减去这两个区间后，又多剪了一个区间\((x+1,y-1)\)，最终需要再加上，因此，最后的答案为：

\[\begin{align*} ans &=f(x,y)-f(x+1,y)-f(x,y-1)+f(x+1,y-1) \end{align*} \]

函数\(f\)

我们可以选用双指针去得到在\((x,y)\)之间的所有数量，右指针\(r\)一直向后移动，直到遇到某数字在\((x,y)\)之外，这时左指针再放到右指针后面。

每次移动右指针，其答案数量都可以看作以\(r\)为右边界，从\(l\)到\(r\)的任意一个数字为左边界，答案变化为\(r-l+1\)。

AC CODE

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+7;
ll a[N];
int n;

ll work(ll y, ll x) {
	ll ans = 0;
	for(int i = 1, j = 1 ; i <= n ; i++) {
		if(a[i] < y || a[i] > x)
			j = i+1;
		ans += i-j+1;
	}
	return ans;
}

int main() {
	int x,y;
	cin >> n;
	cin >> x >> y;
	for(int i = 1 ; i <= n ; i++)
		scanf("%lld",&a[i]);
	ll all = work(y,x),t1 = work(y+1,x),t2 = work(y,x-1), t3 = work(y+1,x-1);
	cout << all-t1-t2+t3;	
}