习题 \(2.1\)
第 \(1\) 题:如何仅用十进制有限小数加减乘运算得到 \(\sqrt{2}\) 的给定精度的近似值?
不懂,没有出发还不能二分(?)
第 \(2\) 题:用定义证明:若 \(f, g\) 都在 \(x_0\) 处连续,且 \(g(x_0)\ne 0\),则 \(f /g\) 在 \(x_0\) 处连续。
由于有连续函数乘法的连续性,因此只需要证明 \(h(x)=\frac{1}{g(x)}\) 在 \(x_0\) 处连续的即可。
\(\forall \epsilon>0\),一定存在 \(\epsilon'\) 满足 \(\epsilon'<|g(x)|\) 且 \(|\frac{1}{g(x)-\epsilon'}-\frac{1}{g(x)}|<\epsilon\),\(|\frac{1}{g(x)+\epsilon'}-\frac{1}{g(x)}|<\epsilon\)。
\(g\) 函数对于 \(\epsilon'\),一定存在 \(\delta\),因此 \(h\) 函数连续。
第 \(3\) 题:设 \(f_1, \ldots, f_n \in \mathcal{C}(I)\),记 \(g(x) = \max\{f_1(x), \ldots, f_n(x)\}\)。证明 \(g \in \mathcal{C}(I)\)。
\(\forall \epsilon>0,\forall i\in [1,n],\exists \delta_i\)。取 \(\delta=\min_{i=1}^{n}\{\delta_i\}\)。
因此对于 \(|x'-x|<\delta\),\(g(x)-\epsilon=\max\{f_1(x)-\epsilon,\cdots,f_n(x)-\epsilon\}< \max\{f_1(x'),\cdots,f_n(x')\}<\max\{f_1(x)+\epsilon,\cdots,f_n(x)+\epsilon\}=g(x)+\epsilon\)。
第 \(4\) 题. 乘方和开方的连续性。用定义证明对任何正整数 \(n\)、\(x^n\) 和 \(x^{\frac{1}{n}}\) 都是区间 \((0, +\infty)\) 上的连续函数。分别对 \(f(x) = x^n\) 和 \(f(x) = x^{\frac{1}{n}}\) 判断是否对任意 \(\varepsilon > 0\) 都存在与 \(x_0 > 0\) 无关的正数 \(\delta\) 使得只要正数 \(x\) 满足 \(|x - x_0| < \delta\) 就有 \(|f(x) - f(x_0)| < \varepsilon\)。
若 \(n=1\),则 \(\forall \epsilon>0\),取 \(\delta=\epsilon\) 即可。
若 \(n>1\),则 \(\forall \epsilon>0\),对于 \(f(x)=x^{\frac{1}{n}}\),取 \(\delta=\epsilon\) 即可。
但对于 \(f(x)=x^n\),不存在与 \(x\) 无关的 \(\delta\),因为 \((x+p)^n-x^n\ge px^{n-1}\),因此若存在 \(\delta\),则有 \(\forall x, \delta x^{n-1}\le \epsilon\),\(x\le \sqrt[n-1]{\frac{\epsilon}{\delta}}\),与阿基米德原理矛盾。
第 \(5\) 题:对数函数的连续性。证明:对 \(a > 1\),对数函数 \(\log_a : \mathbb{R}^+ \to \mathbb{R}\)(定义见习题 1.4)是连续函数。
由于对数函数单调满射,因此连续。
第 \(6\) 题:以下论证希望表明任何增函数都是连续函数。
证明. 设 \(f : (a, b) \to (c, d)\) 是一个增函数。任取 \(x_0 \in (a, b)\)。对任意 \(\varepsilon > 0\),取 \(x_\pm\) 使得 \(f(x_\pm) = f(x_0) \pm \varepsilon\) 以及 \(\delta = \min\{x_+ - x_0, x_0 - x_-\}\)。则 \(x_- < x_0 < x_+\),\(\delta > 0\),且对任意 \(x \in (x_0 - \delta, x_0 + \delta)\),
\[f(x_0) - \varepsilon = f(x_-) < f(x) < f(x_+) = f(x_0) + \varepsilon.
\]
因此 \(f\) 在 \(x_0\) 处连续。
请问上述结论对吗?这个证明对吗?如果你发现这个证明有问题,你能够把它修改成一个正确的证明吗?
不一定存在这样的 \(f(x_\pm) = f(x_0) \pm \varepsilon\)。
应该把条件改成单调满射,这样就对了。
第 \(7\) 题:以下论证希望表明 \(x^2\) 是连续函数。
对于 \(a \in \mathbb{R}\),任取正数 \(\varepsilon\) (\(0 < \varepsilon < a^2\)),当
\[|x - a| < \min \left\{ \sqrt{a^2 + \varepsilon} - a, a - \sqrt{a^2 - \varepsilon} \right\}
\]
时,
\[\sqrt{a^2 - \varepsilon} - a < x - a < \sqrt{a^2 + \varepsilon} - a,
\]
从而
\[\sqrt{a^2 - \varepsilon} < x < \sqrt{a^2 + \varepsilon},
\]
因此
\[a^2 - \varepsilon < x^2 < a^2 + \varepsilon,
\]
于是 \(|x^2 - a^2| < \varepsilon\),所以 \(x^2\) 在 \(x = a\) 处连续。
请问:这个论证有问题吗?
\(\delta\) 的取值不应该和 \(a\) 有关。
第 \(8\) 题:设 \(f: \mathbb{R} \to \mathbb{R}\) 满足对任意 \(x, y \in \mathbb{R}\),
\[f(x + y) = f(x) + f(y).
\]
(1) 证明:对任意 \(x \in \mathbb{Q}\), \(f(x) = f(1)x\)。
首先 \(f(0+0)=f(0)+f(0)\),因此 \(f(0)=0=0f(0)\)。
令 \(A=\{x\in \N|f(x)=f(1)x\}\)。
显然 \(0\in A\)。若 \(x\in A\),则 \(f(x+1)=f(x)+f(1)=f(1)(x+1)\),所以 \(x+1\in A\)。
因此 \(A=\N\)。
对于任意 \(n\in \Z=a-b, a,b\in \N\),有 \(f(a)=f(n)+f(b)\),因此 \(f(n)=f(a)-f(b)=f(1)(a-b)=f(1)n\)。
令 \(A=\{y\in \N|\forall x\in \R,f(xy)=yf(x)\}\)。
显然 \(0\in A\)。若 \(y\in A\),则 \(f(x(y+1))=f(xy+x)=f(xy)+f(x)=yf(x)+f(x)=(y+1)f(x)\)。
因此 \(A=\N\)。
所以 \(f(\frac{x}{y})=xf(\frac{1}{y})=\frac{x}{y}(yf(\frac{1}{y}))=\frac{x}{y}(yf(\frac{1}{y}))=\frac{x}{y}f(1)\)。
(2) 证明:若 \(f\) 连续,则对任意 \(x \in \mathbb{R}\), \(f(x) = f(1)x\)。
(2) 若 \(f(x)<f(1)x\),则 \(\exist \epsilon >0,\epsilon< f(1)x-f(x),\forall \delta >0, \exist x'\in \mathbb{Q},x'>x,0<|x'-x|<\epsilon, f(x')=f(1)x'>f(1)x\),因此 \(f(x')-f(x)>\epsilon\)。
(3) 证明:若 \(f\) 单调,则 \(f\) 连续。
(3) 不妨假设 \(f\) 单调不降。
若 \(f(1)=0\)。若 \(f(x)< 0\),则 \(\exist y\in \mathbb{Q}, y<x\),有 \(f(y)=0>f(x)\),这与 \(f\) 单调不降矛盾;对于 \(f(x)>0\) 同理。
若 \(f(1)\ne 0\),显然有 \(f(1)>0\)。若 \(f(x)<xf(1)\),则 \(\exist y\in \mathbb{Q}, \frac{f(x)}{f(1)}<y<x\),于是 \(f(y)>f(x)\),这与 \(f\) 单调不降矛盾;对于 \(f(x)>xf(1)\) 同理。
因此 \(f(x)=xf(1)\),由于 \(f(x)=x\) 和 \(f(x)=f(1)\) 都是连续函数,因此 \(f(x)=f(1)x\) 也是连续函数。
第 \(9\) 题:设 \(f : \mathbb{R} \to \mathbb{R}\) 连续,且满足对任意 \(x, y \in \mathbb{R}\),
\[f(\sqrt{x^2 + y^2}) = f(x)f(y).
\]
证明对任意 \(x \in \mathbb{R} \setminus \{0\}\),\(f(x) = (f(1))^{x^2}\)。
取 \(x=0,y=0\),则有 \(f(0)=f(0)^2\),因此 \(f(0)\) 为 \(0\) 或 \(1\)。
若 \(f(0)=0\),则 \(\forall t\in \mathbb{R}^+\),取 \(x=t,y=0\),\(f(t)=f(t)f(0)=0\),因此 \(f(t)=0\)。取 \(x=-t,y=0\),\(f(t)=f(-t)f(0)\),因此 \(f(-t)=0\),因此全为 \(0\),自然满足 \(f(x)=(f(1))^{x^2}\) 的条件。
若 \(f(0)=1\),则 \(\forall t\in \mathbb{R}^+\),取 \(x=-t,y=0\),\(f(t)=f(-t)f(0)\),因此 \(f(-t)=f(t)\)。
令 \(g(x^2)=f(x)\),因此有 \(g\) 函数连续,\(\forall x,y\ge 0\),则有 \(g(x^2+y^2)=g(x^2)g(y^2)\),令 \(x'=\sqrt{x}, y'=\sqrt{y}\),那么 \(g(x'+y')=g(x')g(y')\),因此 \(\forall x,y\ge 0\),则有 \(g(x+y)=g(x)g(y)\)。
令 \(h(x)=\ln g(x)\),因此有 \(h\) 函数连续,于是有 \(\forall x,y\ge 0,h(x+y)=h(x)+h(y)\)。
又有 \(h(x)\) 连续,所以 \(h(x)=h(1)x\)。
因此 \(g(x)=e^{h(1)x}=(e^{h(1)})^{x}=g(1)^x\)。
因此 \(f(x)=g(x^2)=g(1)^{x^2}=f(1)^{x^2}\)。
第 \(10\) 题:设 \(f : \mathbb{R} \to \mathbb{R}\) 在任何有界闭区间上有界,且满足中点凸条件,即对任意 \(x, y \in \mathbb{R}\),
\[f\left( \frac{x + y}{2} \right) \leq \frac{f(x) + f(y)}{2}.
\]
证明 \(f\) 是连续函数。
先证明:对任意有理数 \(t \in [0, 1]\),以及任意 \(x, y \in \mathbb{R}\) 都有
\[f((1 - t)x + ty) \leq (1 - t)f(x) + tf(y)
\]
先证明:对任意有理数 \(\frac{x}{2^n}\) 满足条件。
令集合 \(A=\{n\in \N|\forall x\in \N, 0<x<2^n,\forall a_1,a_2,\cdots,a_{2^n}\in \R, f(\frac{\sum_{i=1}^{2^n}a_i}{2^n})\le \frac{\sum_{i=1}^{2^n}f(a_i)}{2^n}\}\)。
\(2\in A\)。
若 \(n\in A\),则:
\[\begin{align}
\frac{\sum_{i=1}^{2^{n+1}}f(a_i)}{2^{n+1}}&= \frac{\sum_{i=1}^{2^n}f(a_{2i-1})+f(a_{2i})}{2^{n+1}}\\
&\ge \frac{\sum_{i=1}^{2^n}2f(\frac{a_{2i-1}+a_{2i}}{2})}{2^{n+1}}\\
&= \frac{\sum_{i=1}^{2^n}f(\frac{a_{2i-1}+a_{2i}}{2})}{2^{n}}\\
&\ge f(\frac{\sum_{i=1}^{2^n}\frac{a_{2i-1}+a_{2i}}{2}}{2^{n}})\\
&= f(\frac{\sum_{i=1}^{2^n}{a_{2i-1}+a_{2i}}}{2^{n+1}})\\
&= f(\frac{\sum_{i=1}^{2^{n+1}}{a_i}}{2^{n+1}})\\
\end{align}
\]
因此 \(n+1\in A\),因此 \(A=\N\)。
对任意有理数 \(\frac{p}{q}\),取正整数 \(m\) 满足 \(2^m\ge q\),令 \(\forall i\le q,a_i=[i\le p]\),\(\forall i>q,a_i=\frac{p}{q}\)。
那么有
\[\begin{align}
\frac{\sum_{i=1}^{2^m} f(a_i)}{2^m}&\ge f(\frac{\sum_{i=1}^{2^m}a_i}{2^m})\\
\frac{(2^m-q)f(\frac{p}{q})+\sum_{i=1}^{q} f(a_i)}{2^m}&\ge f(\frac{p}{q})\\
\frac{\sum_{i=1}^{q} f(a_i)}{2^m}&\ge \frac{qf(\frac{p}{q})}{2^m}\\
\sum_{i=1}^{q} f(a_i)&\ge qf(\frac{p}{q})\\
\frac{\sum_{i=1}^{q} f(a_i)}{q}&\ge f(\frac{p}{q})\\
\end{align}
\]
因此对任何有理数 \(\frac{p}{q}\) 都成立。
证明:若 \(f\) 局部有界,则 \(f\) 连续。
考虑反证。若 \(f\) 在 \(x\) 处不连续,不妨设在 \(x\) 处有 \(r,M\),满足 \(\forall y,|y-x|<r, |f(y)-f(x)|<M\)。而 \(\exist \epsilon >0,\forall \delta>0, \exist x'\in \mathbb{R}, |x'-x|<\delta, |f(x')-f(x)|>\epsilon\)。
取 \(\delta =\frac{M}{\epsilon}\),因此存在 \(x'\)。不妨假设 \(x'>x\),否则取 \(g(x)=f(-x)\) 即可,令 \(d=x'-x\)。若 \(f(x+d)>f(x)\)。取 \(t=\frac{M}{\epsilon}\),\(\frac{1}{t+1}f(x+(t+1)d)+\frac{t}{t+1}f(x)\ge f(x+d)\)。若 \(f(x+d)<f(x)\),同理向左侧取 \(f(x-td)\) 即可。
那么有 \(f(x+(t+1)d)\ge (t+1) f(x+d)-tf(x)=f(x+d)+t(f(x+d)-f(x))> f(x+d)+t\epsilon>f(x)+M\)。
习题 \(2.2\)
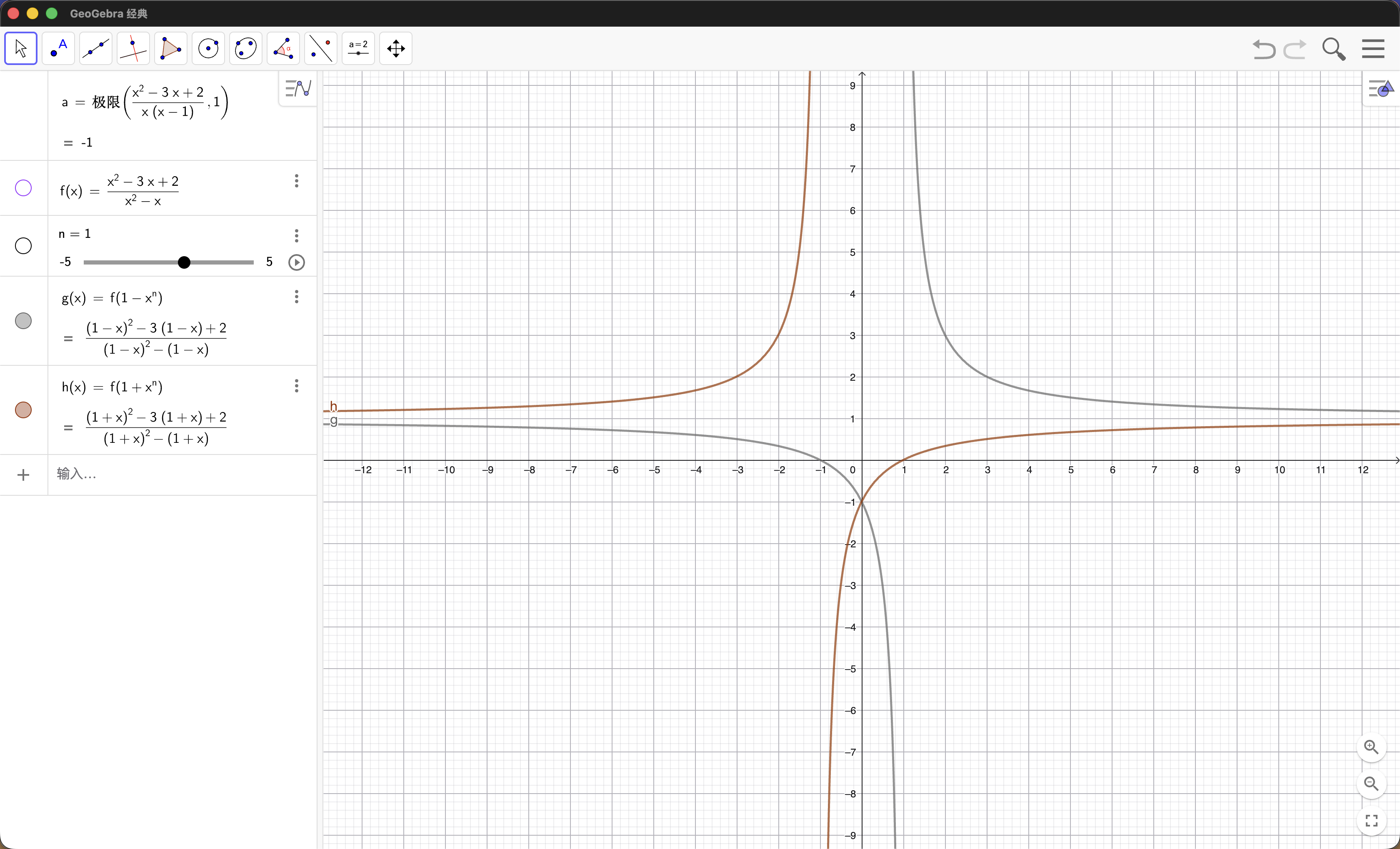
第 \(1\) 题:记 \(f(x) = \frac{x^2 - 3x + 2}{x^2 - x}\),请用 Excel 计算 \(f(1 - 0.1^n)\) 和 \(f(1 + 0.1^n)\),观察并思考其中出现的问题。
第 \(2\) 题:(有理分式与根式,换元及四则运算)求极限
(1) \(\lim_{x \to 2} \frac{x^2 - 3x + 2}{x^3 + x^2 - 6x}\)(提示令 \(h = x - 2\));
(1)
\[\begin{align}
&\lim_{x \to 2} \frac{x^2 - 3x + 2}{x^3 + x^2 - 6x}\\
=&\lim_{x \to 2} \frac{(x-2)(x-1)}{x(x-2)(x+3)}\\
=&\lim_{x \to 2} \frac{(x-1)}{x(x+3)}\\
=&\frac{1}{10}\\
\end{align}
\]
(2) \(\lim_{x \to a} \frac{x^n - a^n}{x - a}\)(\(n\) 是正整数,提示令 \(h = x - a\));
(2)
\[\begin{align}
&\lim_{x \to a} \frac{x^n - a^n}{x - a}\\
=&\lim_{x \to a} \frac{(x-a)(x^{n-1}+x^{n-2}a+\cdots+a^{n-1})}{x - a}\\
=&\lim_{x \to a} x^{n-1}+x^{n-2}a+\cdots+a^{n-1}\\
=&na^{n-1}\\
\end{align}
\]
(3) \(\lim_{x \to a} \frac{x^{m/n} - a^{m/n}}{x-a}\) (\(m, n\) 是正整数,提示令 \(y = \sqrt[n]{x}\));
(3)
令 \(y=x^{\frac{1}{n}}\)。
\[\begin{align}
&\lim_{x \to a} \frac{x^{m/n} - a^{m/n}}{x-a}\\
=&\lim_{y \to a^{\frac{1}{n}}} \frac{y^m - a^m}{y^n - a^n}\\
=&\lim_{y \to a^{\frac{1}{n}}} \frac{(y-a)(x^{m-1}+x^{m-2}a+\cdots+a^{m-1})}{(y-a)(y^{n-1}+y^{n-2}a+\cdots+a^{n-1})}\\
=&\lim_{y \to a^{\frac{1}{n}}} \frac{y^{m-1}+y^{m-2}a+\cdots+a^{m-1}}{y^{n-1}+y^{n-2}a+\cdots+a^{n-1}}\\
=&\frac{m(a^{\frac{1}{n}})^{m-1}}{n(a^{\frac{1}{n}})^{n-1}}\\
=&\frac{m}{n}(a^{\frac{1}{n}})^{m-n}\\
=&\frac{m}{n}a^{\frac{m-n}{n}}\\
=&\frac{m}{n}a^{\frac{m}{n}-1}\\
\end{align}
\]
(4) \(\lim_{x \to 0} \frac{\sqrt{1+x} - \sqrt[3]{1-x}}{x}\);
令 \(y=1+x, z=1-x\)。
\[\begin{align}
&\lim_{x \to 0} \frac{\sqrt{1 + x} - \sqrt[3]{1 - x}}{x}\\
=&\lim_{x \to 0} \frac{\sqrt{1 + x}-1+1 - \sqrt[3]{1 - x}}{x}\\
=&\lim_{x \to 0} \frac{\sqrt{1 + x}-1}{x}+\lim_{x \to 0} \frac{1 - \sqrt[3]{1 - x}}{x}\\
=&\lim_{y \to 1} \frac{\sqrt{y}-1}{y-1}+\lim_{z \to 1} \frac{\sqrt[3]{z}-1}{z-1}\\
=&\frac{1}{2}+\frac{1}{3}\\
=&\frac{5}{6}
\end{align}
\]
(5) \(\lim_{x \to 4} \frac{\sqrt{1+2x}-3}{\sqrt{x-2}}\)。
令 \(a=\frac{2x+1}{9},b=\frac{x}{4}\)。
\[\begin{align}
&\lim_{x \to 4} \frac{\sqrt[3]{3 + 6x} - 3}{\sqrt{x} - 2}\\
=&\lim_{x \to 4} \frac{3(\sqrt[3]{\frac{2x+1}{q}} - 1)}{2(\sqrt{\frac{x}{4}}-1)}\\
=&\frac{3}{2}\lim_{x \to 4} \frac{\sqrt[3]{\frac{2x+1}{9}} - 1}{\sqrt{\frac{x}{4}}-1}\\
=&\frac{3}{2}\lim_{x \to 4} \frac{a^\frac{1}{3}-1}{b^{\frac{1}{2}}-1}\\
=&\frac{3}{2}\lim_{x \to 4} \frac{a^\frac{1}{3}-1}{a-1}\frac{a-1}{b-1}\frac{b-1}{b^{\frac{1}{2}}-1}\\
=&\frac{3}{2}\lim_{x \to 4} \frac{1}{3}\cdot 2\cdot\frac{a-1}{b-1}\\
=&\frac{3}{2}\lim_{x \to 4} \frac{1}{3}\cdot 2\cdot\frac{\frac{2x-8}{9}}{\frac{x-4}{4}}\\
=&\frac{3}{2}\lim_{x \to 4} \frac{1}{3}\cdot 2\cdot\frac{\frac{2}{9}}{\frac{1}{4}}\\
=&\frac{3}{2}\lim_{x \to 4} \frac{1}{3}\cdot 2\cdot\frac{8}{9}\\
=&\frac{8}{9}
\end{align}
\]
三角函数的连续性和重要极限:
\(\lim_{x\rightarrow 0}\sin x=0,\lim_{x\rightarrow 0}\cos x=1,\lim_{x\rightarrow 0}\frac{\sin x}{x}=\frac{\tan x}{x}=\lim_{x\rightarrow 0}\frac{1-\cos x}{x^2}=1\)。
- (三角函数,换元及四则运算)求极限
·
(1) \(\lim_{x \to a} \frac{\sin x - \sin a}{x-a}\) (提示令 \(h = x - a\));
(1) 先证明 \(\lim_{x\rightarrow 0}\frac{\cos x-1}{x}=0\),\(y=\frac{x}{2}\)。
\[\begin{align}
\lim_{x\rightarrow 0}\frac{\cos x-1}{x}=&\lim_{x\rightarrow 0}\frac{-2\sin^2{\frac{x}{2}}}{x}\\
=&\lim_{y\rightarrow 0}\frac{-2\sin^2{y}}{2y}\\
=&-\lim_{y\rightarrow 0}\frac{\sin^2 y}{y}\\
=&-\lim_{y\rightarrow 0}\frac{\sin y}{y}\cdot\lim_{y\rightarrow 0}\sin y\\
=&-1\cdot 0\\
=&0
\end{align}
\]
\(y=x-a,x=a+y\)。
\[\begin{align}
&\lim_{x\rightarrow a} \frac{\sin x-\sin a}{x-a}\\
=&\lim_{y\rightarrow 0} \frac{\sin (a+y)-\sin a}{y}\\
=&\lim_{y\rightarrow 0} \frac{\sin a\cos y+\cos a\sin y-\sin a}{y}\\
=&\cos a(\lim_{y\rightarrow 0} \frac{\sin y}{y})+\sin a(\lim_{y\rightarrow 0} \frac{\cos y-1}{y})\\
=&\cos a
\end{align}
\]
(2) \(\lim_{x \to a} \frac{\cos x - \cos a}{x-a}\) (提示令 \(x = \frac{\pi}{2} - t\));
(2) \(y=x-a,x=a+y\)。
\[\begin{align}
&\lim_{x\rightarrow a} \frac{\cos x-\cos a}{x-a}\\
=&\lim_{y\rightarrow 0} \frac{\cos (a+y)-\cos a}{y}\\
=&\lim_{y\rightarrow 0} \frac{\cos a\cos y-\sin a\sin y-\cos a}{y}\\
=&-\sin a(\lim_{y\rightarrow 0} \frac{\sin y}{y})+\cos a(\lim_{y\rightarrow 0} \frac{\cos y-1}{y})\\
=&-\sin a
\end{align}
\]
(3) \(\lim_{x \to 0} x \cot x\);
(3)
\[\begin{align}
&\lim_{x \to 0} x \cot x\\
=&\lim_{x \to 0} x \frac{\cos x}{\sin x}\\
=&\lim_{x \to 0} x \frac{\cos x}{\sin x}\\
=&(\lim_{x \to 0} \frac{x}{\sin x}) (\lim_{x \to 0}\cos x)\\
=&1
\end{align}
\]
(4) \(\lim_{x \to 0} \frac{\sqrt{\cos x} - \sqrt[3]{\cos x}}{\sin x^2}\);
(4) 先求 \(\lim_{x \to 0}\frac{\cos x - 1}{x^2}\):
\[\begin{align}
&\lim_{x \to 0}\frac{\cos x - 1}{x^2}\\
=&\lim_{x \to 0} \frac{-2\sin^2 \frac{x}{2}}{x^2}\\
=&-\frac{1}{2}\lim_{x \to 0} \frac{\sin^2 y}{y^2} & y=\frac{x}{2}\\
=&-\frac{1}{2}
\end{align}
\]
\[\begin{align}
&\lim_{x \to 0} \frac{\sqrt{\cos x} - \sqrt[3]{\cos x}}{\sin x^2}\\
=&(\lim_{x \to 0} \frac{\sqrt{\cos x} - \sqrt[3]{\cos x}}{x^2})(\lim_{x \to 0}\frac{x^2}{\sin^2 x})\\
=&\lim_{x \to 0} \frac{\sqrt{\cos x} - \sqrt[3]{\cos x}}{x^2}\\
=&\lim_{x \to 0} \frac{\sqrt{\cos x}-1}{x^2}+\lim_{x \to 0} \frac{1 - \sqrt[3]{\cos x}}{x^2}\\
=&\lim_{x \to 0} \frac{\sqrt{\cos x}-1}{x^2}+\lim_{x \to 0} \frac{1 - \sqrt[3]{\cos x}}{x^2}\\
\end{align}
\]
分别求 \(\lim_{x \to 0} \frac{\sqrt{\cos x}-1}{x^2}\):
\[\begin{align}
&\lim_{x \to 0} \frac{\sqrt{\cos x}-1}{x^2}\\
=&\lim_{x \to 0} \frac{\sqrt{\cos x}-1}{\cos x-1}\lim_{x \to 0} \frac{\cos x-1}{x^2}\\
=&\frac{1}{2}\times(-\frac{1}{2})\\
=&-\frac{1}{4}\\
\end{align}
\]
\(\lim_{x \to 0} \frac{1 - \sqrt[3]{\cos x}}{x^2}\):
\[\begin{align}
&\lim_{x \to 0} \frac{1 - \sqrt[3]{\cos x}}{x^2}\\
=&-\lim_{x \to 0} \frac{\sqrt[3]{\cos x}-1}{x^2}\\
=&-\lim_{x \to 0} \frac{\sqrt[3]{\cos x}-1}{\cos x - 1}\lim_{x \to 0}\frac{\cos x - 1}{x^2}\\
=&-\frac{1}{3}\lim_{x \to 0}\frac{\cos x - 1}{x^2}\\
=&-\frac{1}{3}\times(-\frac{1}{2})\\
=&\frac{1}{6}
\end{align}
\]
因此,\(\lim_{x \to 0} \frac{\sqrt{\cos x} - \sqrt[3]{\cos x}}{\sin x^2}=-\frac{1}{4}+\frac{1}{6}=-\frac{1}{12}\)。
(5) \(\lim_{x \to 0} \frac{1 - \cos x \sqrt{\cos 2x} \sqrt[3]{\cos 3x}}{x^2}\);
(5) 令 \(A=\cos x, B=\sqrt{\cos 2x}, C=\sqrt[3]{\cos 3x}\)。
\[\begin{align}
&\lim_{x \to 0} \frac{1 - \cos x \sqrt{\cos 2x} \sqrt[3]{\cos 3x}}{x^2}\\
=&\lim_{x \to 0} \frac{1 - ABC}{x^2}\\
=&\lim_{x \to 0} \frac{(1-A)+A(1-B)+AB(1-C)}{x^2}\\
=&\lim_{x \to 0} \frac{1-A}{x^2}+\lim_{x \to 0} \frac{A(1-B)}{x^2}+\lim_{x \to 0} \frac{AB(1-C)}{x^2}\\
\end{align}
\]
\(\lim_{x \to 0} \frac{1-A}{x^2}\):
\[\begin{align}
&\lim_{x \to 0} \frac{1-A}{x^2}\\
=&\lim_{x \to 0} \frac{1-\cos x}{x^2}\\
=&\lim_{x \to 0} \frac{\cos 0-\cos x}{x^2}\\
=&\lim_{x \to 0} \frac{2\sin^2 \frac{x}{2}}{x^2}\\
=&\lim_{y \to 0} \frac{2\sin^2 y}{4y^2}&y=\frac{x}{2}\\
=&\frac{1}{2}\lim_{y \to 0} \frac{\sin^2 y}{y^2}\\
=&\frac{1}{2}(\lim_{y \to 0} \frac{\sin y}{y})^2\\
=&\frac{1}{2}\\
\end{align}
\]
\(\lim_{x \to 0} \frac{A(1-B)}{x^2}\):
\[\begin{align}
&\lim_{x \to 0} \frac{A(1-B)}{x^2}\\
=&\lim_{x \to 0} \frac{\cos x(1-\sqrt{\cos 2x})}{x^2}\\
=&(\lim_{x \to 0}\cos x)(\lim_{x \to 0} \frac{1-\sqrt{\cos 2x}}{x^2})\\
=&\lim_{x \to 0} \frac{1-\sqrt{\cos 2x}}{x^2}\\
=&4\lim_{y \to 0} \frac{1-\sqrt{\cos y}}{y^2}&y=2x\\
=&4\lim_{y \to 0} \frac{1-\cos y}{y^2(1+\sqrt{\cos y})}\\
=&4\lim_{y \to 0} \frac{1-\cos y}{y^2}\lim_{y \to 0}\frac{1}{1+\sqrt{\cos y}}\\
=&4\times \frac{1}{2}\times\frac{1}{2}\\
=&1
\end{align}
\]
\(\lim_{x \to 0} \frac{AB(1-C)}{x^2}\):
\[\begin{align}
&\lim_{x \to 0} \frac{AB(1-C)}{x^2}\\
=&\lim_{x \to 0} \frac{\cos x\sqrt{\cos 2x}(1-\sqrt[3]{\cos 3x})}{x^2}\\
=&\lim_{x \to 0} \cos x\lim_{x \to 0} \sqrt{\cos 2x}\lim_{x \to 0} \frac{1-\sqrt[3]{\cos 3x}}{x^2}\\
=&\lim_{x \to 0} \frac{1-\sqrt[3]{\cos 3x}}{x^2}\\
=&9\lim_{x \to 0} \frac{1-\sqrt[3]{\cos y}}{y^2}&y=3x\\
=&9\lim_{x \to 0} \frac{1-\cos y}{y^2(1+(\cos y)^{\frac{1}{3}}+(\cos y)^{\frac{2}{3}})}\\
=&9\lim_{x \to 0} \frac{1-\cos y}{y^2}\lim_{x\to 0}\frac{1}{1+(\cos y)^{\frac{1}{3}}+(\cos y)^{\frac{2}{3}}}\\
=&9\times\frac{1}{2}\times\frac{1}{3}\\
=&\frac{3}{2}
\end{align}
\]
因此 \(\lim_{x \to 0} \frac{1 - \cos x \sqrt{\cos 2x} \sqrt[3]{\cos 3x}}{x^2}=\frac{1}{2}+1+\frac{3}{2}=3\)。
(6) \(\lim_{x \to \frac{\pi}{3}} \frac{\tan^3 x - 3 \tan x}{\cos(x + \frac{\pi}{6})}\) (提示令 \(h = x - \frac{\pi}{3}\))。
(6) 令 \(h=x-\frac{\pi}{3}\),则 \(x=h+\frac{\pi}{3}\)。
\[\begin{align}
&\lim_{x \to \frac{\pi}{3}} \frac{\tan^3 x - 3 \tan x}{\cos(x + \frac{\pi}{6})}\\
=&(\lim_{x \to \frac{\pi}{3}} \tan x)(\lim_{x \to \frac{\pi}{3}} \frac{\tan^2 x - 3}{\cos(x + \frac{\pi}{6})})\\
=&\sqrt{3}(\lim_{x \to \frac{\pi}{3}} \frac{\tan^2 x - 3}{\cos(x + \frac{\pi}{6})})\\
=&\sqrt{3}\lim_{h \to 0} \frac{\tan^2 (h+\frac{\pi}{3}) - 3}{\cos(h + \frac{\pi}{2})}\\
=&\sqrt{3}\lim_{h \to 0} \frac{\tan^2 (h+\frac{\pi}{3}) - 3}{-\sin(h)}\\
=&-\sqrt{3}\lim_{h \to 0} \frac{\tan^2 (h+\frac{\pi}{3}) - 3}{h}\lim_{h \to 0}\frac{h}{\sin h}\\
=&-\sqrt{3}\lim_{h \to 0} \frac{\tan^2 (h+\frac{\pi}{3}) - 3}{\tan h}\lim_{h\to 0} \frac{\tan h}{h}\\
=&-\sqrt{3}\lim_{h \to 0} \frac{(\frac{\sqrt{3}+\tan h}{1-\sqrt{3}\tan h})^2 - 3}{\tan h}\\
=&-\sqrt{3}\lim_{y \to 0} \frac{(\frac{\sqrt{3}+y}{1-\sqrt{3}y})^2 - 3}{y}&y=\tan h\\
=&-\sqrt{3}\lim_{y \to 0} \frac{(3+2\sqrt{3}y+y^2) - (3-6\sqrt{3}y+9y^2)}{y(1-2\sqrt{3}y+3y^2)}\\
=&-\sqrt{3}\lim_{y \to 0} \frac{8\sqrt{3}y-8y^2}{y(1-2\sqrt{3}y+3y^2)}\\
=&-\sqrt{3}\lim_{y \to 0} \frac{8\sqrt{3}-8y}{1-2\sqrt{3}y+3y^2}\\
=&-\sqrt{3}\times(\frac{8\sqrt{3}}{1})\\
=&-24\\
% =&-\sqrt{3}\lim_{h \to 0} \frac{\tan^2 (h+\frac{\pi}{3}) - \tan^2 \frac{\pi}{3}}{h}\\
% =&-\sqrt{3}\lim_{h \to 0} \frac{(\tan (h+\frac{\pi}{3}) +\tan \frac{\pi}{3})(\tan (h+\frac{\pi}{3}) -\tan \frac{\pi}{3})}{h}\\
% =&-\sqrt{3}\lim_{h \to 0} \frac{\tan (h+\frac{2}{3\pi})(1-\tan (h+\frac{\pi}{3})\tan h)\tan h(1+\tan (h+\frac{\pi}{3})\tan h)}{h}\\
\end{align}
\]




 浙公网安备 33010602011771号
浙公网安备 33010602011771号