布隆过滤器（Bloom Filter）详解及应用

1 位图（BitMap）

在讨论布隆过滤器之前，先看一下位图是什么。

首先考虑一个问题场景

假如需要过滤某些不安全网页，现有100亿个黑名单页面，每个网页的URL最多占用64字节。现要设计一种网页过滤系统，可以根据网页的URL判断该网页是否在黑名单上。

最直观的想法必然是使用一个集合或者说数据结构来存放黑名单URL，比如查找树、Set、map，但是无论哪种，不可避免的是我们需要存储原始的URL值，但是我们都知道URL并不是一个很短的字符串，动辄十几/几十字节，假设一个URL有30字节那么100亿URL所占内存就是十几G，所以每次判断是否存在于黑名单中，就要占用很大的内存开销。

但是，我们需要的仅仅是知道是否存在这一需求，可以不需要具体的URL，所以仅仅对Ture or False 这个问题，可以使用位图（BitMap）算法，位图顾名思义就是，每个map值都使用1bit，这样大大降低了内存开销，具体做法是，我们使用一个Hash函数将URL映射到大小为n的bit数组中，并置相应位置为True

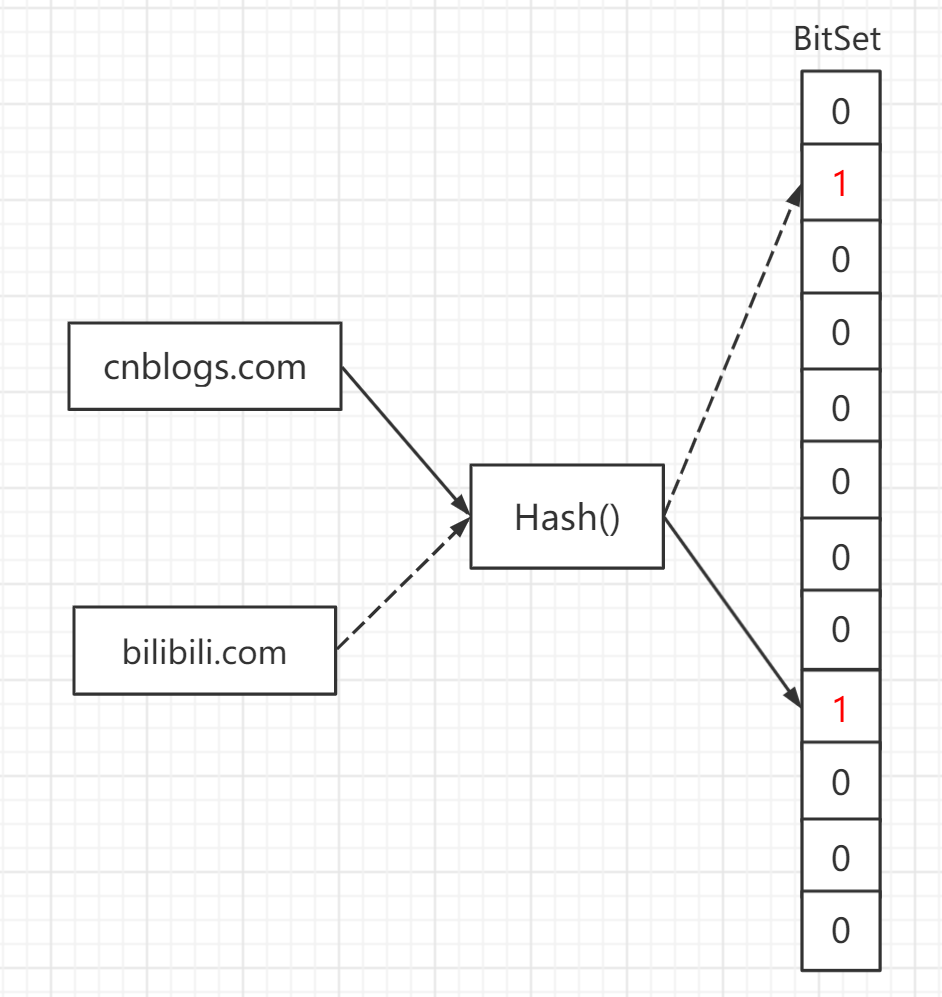
这样我们可以在尽可能低的内存开销下，实现O（1）时间的判断URL是否存在黑名单中。

但不得不面对的一个问题就是，即使采取再好的哈希函数，都会出现哈希冲突的情况，在查询阶段出现哈希冲突意味着查询错误，会返回一个错误的结果，而想尽可能的降低哈希冲突，我们需要位图大小比黑名单中URL数量大的多，我们考虑随机哈希的情况下，查询碰撞的概率是：黑名单URL数量/位图大小。所以要想查询准确率高，又带来了更高的内存开销，而可以有效改善这种情况的一种数据结构叫做布隆过滤器（Bloom Filter）。

2 布隆过滤器（Bloom Filter）

2.1 是什么

考虑位图情况出现的问题：在有限的比特数组大小下，碰撞概率会很高，布隆过滤器解改善了这个问题，具体的，它使用多个Hash函数对数据进行哈希操作（如下图使用了两个hash函数），这样得出多个位置为True，相比位图它在有限的空间内，尽可能的降低了查询失败的可能，这一点可以从信息熵的角度来看，每一个位置所包含的信息更加多了，所以比起位图来说，布隆过滤器对空间的利用率也变大了，当然这一点也会带来别的坏处下面会说到。

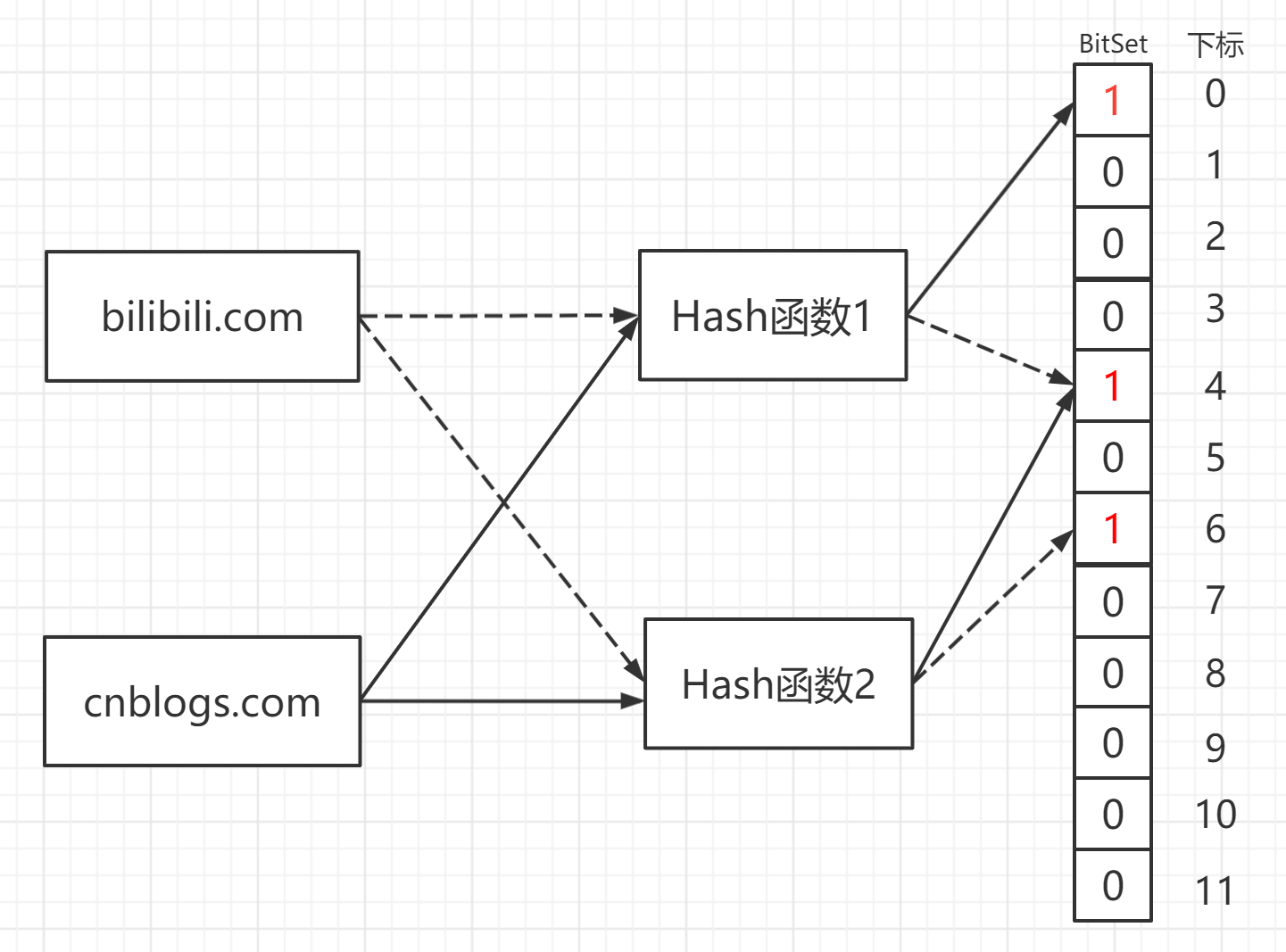
以上图为例，假设对bilibli.com进行两次hash运算

\[Hash_1(bilibli.com) \% 12 = 4 \]

\[Hash_2(bilibli.com) \% 12 = 6 \]

得到结果后，令BitSet数组中下标为4和6的位置1，同样对cnblogs.com进行两次hash计算映射到数组中下标0和4的位置，置1，那么假如来一条查询信息，只需要同样计算两次哈希，若同时为1，则返回true即可。

而实际操作中，哈希函数一般会选取多个，比如常用的8个哈希函数，尽可能的在有限的空间内降低查询出现哈希冲突的可能，但是冲突现象显然是无法避免的，只能根据需求，通过合理的选择位数组的大小以及哈希函数来尽可能降低冲突率。

上面谈到，布隆过滤器每个位置不再标识一条数据，可能标识多条数据，因而对于bit数组中的某个位置来讲，它的值信息熵更大了，但是既然一个位置可以标识多条数据，正所谓牵一发而动全身，所以布隆过滤器也就存在的一个问题，无法对黑名单进行删除操作，比如上述的例子，下标为4的位置是两条数据经过不同的哈希运算后得到了同样的结果，假如要删除一条数据必然影响其他数据的查询结果，造成更高的误判率。

2.2 误判率

布隆过滤器的误判率也可以称之为假阳性（false positive）的概率，比如来一条URL查询是否在黑名单中，结果其对应的哈希结果已经被其他一个或者多个URL置1，那么此时就出现了查询错误的情况。所以布隆过滤器只适合有内存开销限制、并且允许出现错误率的情况，我们可以通过分析其出现错误的概率，选取合适的bit数组大小以及哈希函数，尽可能在内存开销和错误率中间进行一个折中的选择，下面分析一下布隆过滤器的误判率。

假设bit数组大小为m，数据量为n，使用k个不同的哈希函数映射，那么考虑随机哈希情况下，数组中某一个位置在一次哈希后被置1的概率为

\[\frac1m \]

那么在一次哈希过后，数组中某一位为0的概率即为

\[1-\frac1m \]

经过k个哈希函数后，某一个位置为0的概率即为

\[(1-\frac1m)^k \]

考虑m足够大的情况下有

\[\lim\limits_{m\rightarrow\infty}(1-\frac1m)^m=\frac1e \]

所以有k个哈希函数后，某一个位置为0的概率即为

\[(1-\frac1m)^k\approx e^{\frac{-k}{m}} \]

则插入n个数后，某个位置仍然为0的概率为

\[(1-\frac1m)^{kn}\approx e^{\frac{-kn}{m}} \]

所以插入n个数后，bit数组中某个位置为1的概率为

\[1-e^{\frac{-kn}{m}} \]

所以在插入n个数后，来一条查询数据，数据经过k个哈希函数映射后，bit数组中k个位置均为1的概率为：

\[P\approx (1-e^{\frac{-kn}{m}})^k \]

P即为布隆过滤器，将n条数据，进行k次哈希后，存入大小为m的bit数组后，再查询一条数据，出现误判（数据不存在，却误以为存在）的概率。

所以根据这个概率，在考虑设计布隆过滤器时，假如已给定大致的数据总量n，我们就可以通过调整m和k的大小来尽可能的得到较低的误判率也就是概率P，下面给出部分概率参考。（表格参考 http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html ，里面也有简单的概率推导以及更加详细的表格）

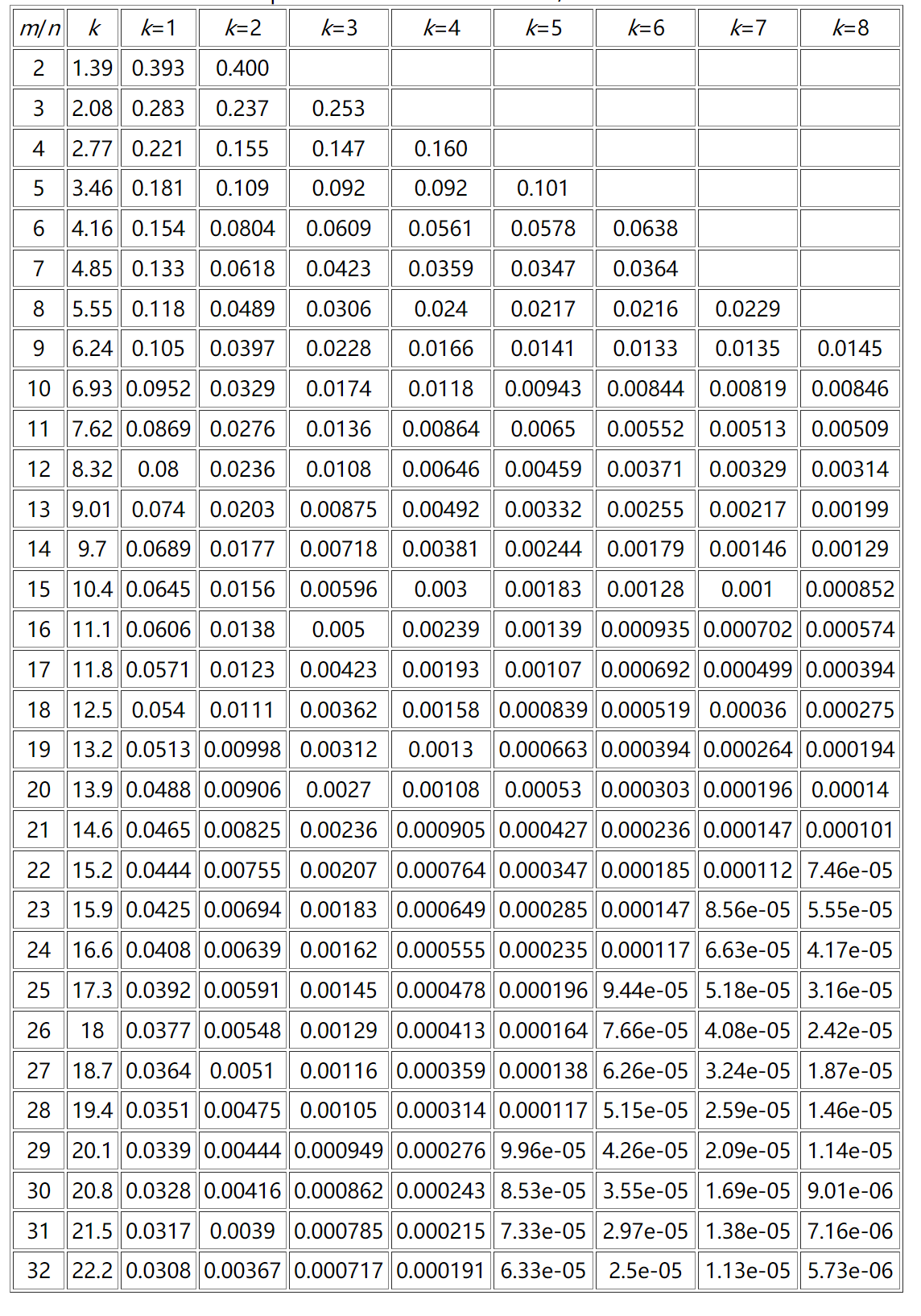
观察上表可以看出，假设m/n为16的情况下，即每条数据使用16bit大小的空间，我们使用8个哈希函数映射，此时误判率已经到了0.0005，也就是万分之5，回到开头的URL黑名单问题，我们上面假设一条URL有40字节也就是320比特，假如使用布隆过滤器来做黑名单问题，相当于只用了存储每条URL情况的二十分之一甚至更低，带来了万分之五的错误率，而其复杂度也很低，因为只需要经过几次简单的哈希运算。

2.3 使用（以Java为例）

了解了原理后使用布隆过滤器你可以自行设计，也可以使用Google 开源的 Guava 中自带的布隆过滤器，这里简单介绍一下它的使用，首先需要引入依赖

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>28.0-jre</version>
</dependency>

创建一个布隆过滤器

BloomFilter<String> filter = BloomFilter.create(
	Funnels.stringFunnel(Charset.defaultCharset()),
	1000,
	0.001);

其中第create函数的2、3个参数，可以显式的控制数据量和误判率，其就是通过本文2.3中讲到的误判率那样操作。

添加数据和判断是否存在

filter.put("bilibili.com");
filter.put("cnblogs.com");

System.out.println(filter.mightContain("bilibili.com"));
System.out.println(filter.mightContain("zhihu.com"));

上面设置的误判率是0.001，所以当mightContain()函数返回true时，我们可以99.9%的确认，判断的数据存在于布隆过滤器中。它的缺陷就是不能进行删除操作，而且只能单机使用。

另外分布式环境下，Redis中也可以使用布隆过滤器，Redis v4.0 之后有了 Module 功能，可以使用官方推荐的第三方布隆过滤器插件https://github.com/RedisBloom/RedisBloom。

2.4 实际应用

海量数据下，通过设计正确适用的布隆过滤器以很低的错误率带来了几十倍的内存开销降低，其应用范围也很广，比如

• 识别恶意邮箱地址。
• URL黑名单、白名单，比如Chrome浏览器就是使用了一个布隆过滤器识别恶意链接。
• 解决缓存穿透问题，缓存穿透指查询一个不存在的数据，这时候缓存中不存在，就会不断的查询数据库，造成不必要的IO，而且有人如果恶意使用不存在的key也可以对数据库进行攻击。
• 果蝇....通过改进的布隆过滤器来检测新鲜气味。（混入一个奇怪的东西）
• 谷歌Bigtable、Apache HBase、Apache Cassandra和PostgreSQL使用布隆过滤器来减少对不存在的行或列的磁盘查找。
• ......

3 布谷鸟过滤器

https://www.cnblogs.com/zhaodongge/p/15067657.html