初学线段树

这是我初学线段树时的一些学习记录，主要参考了其他一些博客（见参考文章），再加上基本的代码实现

一、线段树的概念

线段树擅长处理区间，树上的每个节点都维护一个区间，根维护的是整个区间，每个节点维护的是父亲节点区间二等分后的其一子区间。当有n个元素时，对区间的操作可以在O（log n）时间内完成。

 

二、线段树可处理的问题

区间最值，区间求和O(log n)内完成，等具有区间加法的性质的问题

区间加法：可通过将问题分解成若干子问题后合并得出最终结果，如区间和=左区间和+右区间和，区间最值=左区间最值+右区间最值

不符合区间加法，如求整个区间的众数，整个区间的最长连续0等

三、直观理解

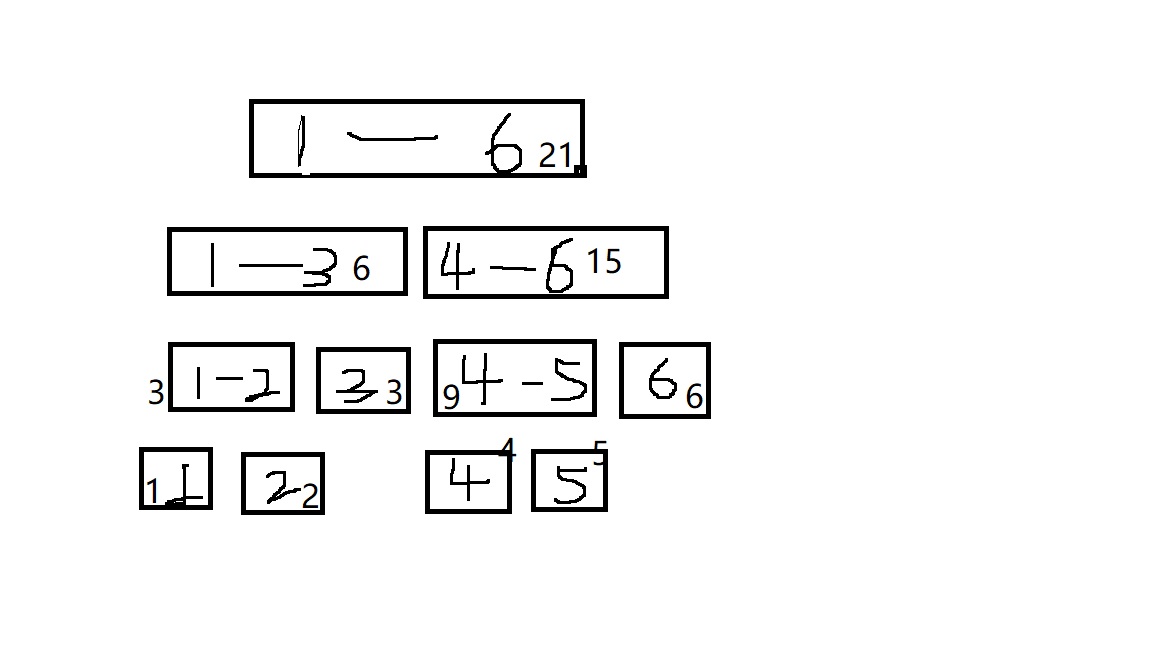
注：区间的data域为区间和

四、实现

（1）建树

此处为结构体数组，关于数组大小：

  由于线段树是一种二叉树，所以当区间长度为2的幂时，它正好是一棵满二叉树，数组存储的利用率达到最高（即100%），根据等比数列求和可以得出，满二叉树的结点个数为2*n-1（n为叶节点个数，也为输入数据的个数）。那么是否对于所有的区间长度n都满足这个公式呢？答案是否定的，当区间长度为6时，最大的结点编号为13（包括没有数据的叶节点，因为是数组存储，该出占了空间但未使用），而公式算出来的是12（2*6）。
    那么 数组大小取多少合适呢？
    为了保险起见，我们可以先找到比n大的最小的二次幂，然后再套用等比数列求和公式，这样就万无一失了。举个例子，当区间长度为6时，max_n= 2 * 8；当区间长度为1000，则max_n = 2 * 1024；当区间长度为10000，max_n = 2 * 16384。一般取四倍空间，即n<<2.

#include <iostream>
#define max_n 1000
using namespace std;
struct treeNode
{
    int data; //数据域，再次存放需要数据，此处为区间和
    int lz; //懒惰标记，表示该区间已更新数据，但其子区间的数据还没更新
};
treeNode node[max_n]; //数组表示整棵树，下标从1开始
int input[max_n] = {0,1,2,3,4,5,6}; //此为模拟的输入数据

void pushup(int p) //在向上回溯时更新当前节点的data域，此处为求子区间的和
{
    node[p].data= node[p<<1].data+node[p<<1|1].data;
}
void build_tree(int p,int l,int r)
{
    if(l==r) //若只有一个节点，则为叶节点，将数据填入
    {
        node[p].data = input[l]; 
        node[p].lz = 0;
        return;
    }

    int mid = (l+r)>>1; 
    build_tree(p<<1,l,mid); //递归地构建左子树，此处将中间节点划分为左子树部分，与下面在分叉时的条件相对应
    build_tree(p<<1|1,mid+1,r); //递归地构建右子树
    pushup(p);//回溯时更新当前数据域
}

（2）点修改

 1 void pmodify(int p,int l,int r,int val) //l为当前区间节点左端点，r为相应的右端点
 2 {
 3     if(l==r) //到达该点
 4     {
 5         node[p].data = val;//修改值
 6         return;
 7     }
 8     int mid = (l+r)>>1; //若未到达，利用二分
 9     if(p<=mid) pmodify(p,l,mid,val);//递归搜索左子树
10     else pmodify(p,mid+1,r,val);//递归搜索右子树
11     pushup(p);//搜索完后更新值
12 }

（3）关于懒惰标记

线段树的区间修改也是将区间分成子区间，但是要加一个标记，称作懒惰标记。
标记的含义：
本节点的统计信息已经根据标记更新过了，但是本节点的子节点仍需要进行更新。
即，如果要给一个区间的所有值都加上1，那么，实际上并没有给这个区间的所有值都加上1，而是打个标记，记下来，这个节点所包含的区间需要加1.打上标记后，要根据标记更新本节点的统计信息，比如，如果本节点维护的是区间和，而本节点包含5个数，那么，打上+1的标记之后，要给本节点维护的和+5。这是向下延迟修改，但是向上显示的信息是修改以后的信息，所以查询的时候可以得到正确的结果。有的标记之间会相互影响，所以比较简单的做法是，每递归到一个区间，首先下推标记（若本节点有标记，就下推标记），然后再打上新的标记，这样仍然每个区间操作的复杂度是O(log2(n))。

标记有相对标记和绝对标记之分：
相对标记是将区间的所有数+a之类的操作，标记之间可以共存，跟打标记的顺序无关（跟顺序无关才是重点）。
所以，可以在区间修改的时候不下推标记，留到查询的时候再下推。
      注意：如果区间修改时不下推标记，那么PushUp函数中，必须考虑本节点的标记。
                 而如果所有操作都下推标记，那么PushUp函数可以不考虑本节点的标记，因为本节点的标记一定已经被下推了（也就是对本节点无效了）
绝对标记是将区间的所有数变成a之类的操作，打标记的顺序直接影响结果，
所以这种标记在区间修改的时候必须下推旧标记，不然会出错。

注意，有多个标记的时候，标记下推的顺序也很重要，错误的下推顺序可能会导致错误。(以上摘自博客，见参考文章）

（4）区间修改和区间查询

 1 void pushdown(int p,int ln,int rn) //下推懒惰标记
 2 {
 3     if(node[p].lz) //如果懒惰标记不为0
 4     {
 5         node[p<<1].lz += node[p].lz; //更新左子树的懒惰标记
 6         node[p<<1|1].lz += node[p].lz;//更新右子树的懒惰标记
 7         node[p<<1].data += ln*node[p].lz;//更新左子树的数据域，因为此时左子树懒惰标记已存在，根据懒惰标记含义，应该更新
 8         node[p<<1|1].data += rn*node[p].lz;//更新右子树的数据域，同上
 9         node[p].lz = 0;//将改节点的懒惰标记清0
10     }
11 }
12 void update(int p,int L,int R,int l,int r,int val)//数据域的处理，[L,R]表示将处理的区间，[l,r]表示当前节点的表示区间
13 { //val在此为在要处理的区间统一要加上的数值
14     if(L<=l&&r<=R)//若当前节点的表示区间完全落在要处理的区间
15     {
16         node[p].data = node[p].data+val*(r-l+1);//更新该区间的数据域
17         node[p].lz = node[p].lz+val;//更新懒惰标记
18         return;
19     }
20     int mid = (l+r)>>1;//此处为利用mid二分区间，最终目标是递归到区间完全包含的情况
21     pushdown(p,mid-l+1,r-mid);//根据懒惰标记定义，下推懒标记
22     if(L<=mid) update(p<<1,L,R,l,mid,val);//目标区间与当前节点的左区间有交集
23     if(mid<R) update(p<<1|1,L,R,mid+1,r,val);//目标区间与当前节点的右区间有交集
24     pushup(p);//回溯时更新当前节点的数据域
25 
26 }
27 int query(int p,int L,int R,int l,int r)//[L,R]为目标区间，[l,r]为当前节点的表示区间
28 {
29     if(L<=l&&r<=R) //同上
30     {
31         return node[p].data;
32     }
33     int mid = (l+r)>>1;
34     pushdown(p,mid-l+1,r-mid);
35     int ans = 0;
36     if(L<=mid) ans += query(p<<1,L,R,l,mid);
37     if(mid<R) ans += query(p<<1|1,L,R,mid+1,r);
38     return ans;
39 }

 

(5)实例：

 1 int main()
 2 {
 3     build_tree(1,1,6);
 4     int ans = query(1,3,5,1,6);
 5     cout << ans << endl;
 6     update(1,3,5,1,6,1);
 7     ans = query(1,3,5,1,6);
 8     cout << ans << endl;
 9     return 0;
10 }

 

现在查询【3,5】的区间和，如图为3+4+5=12

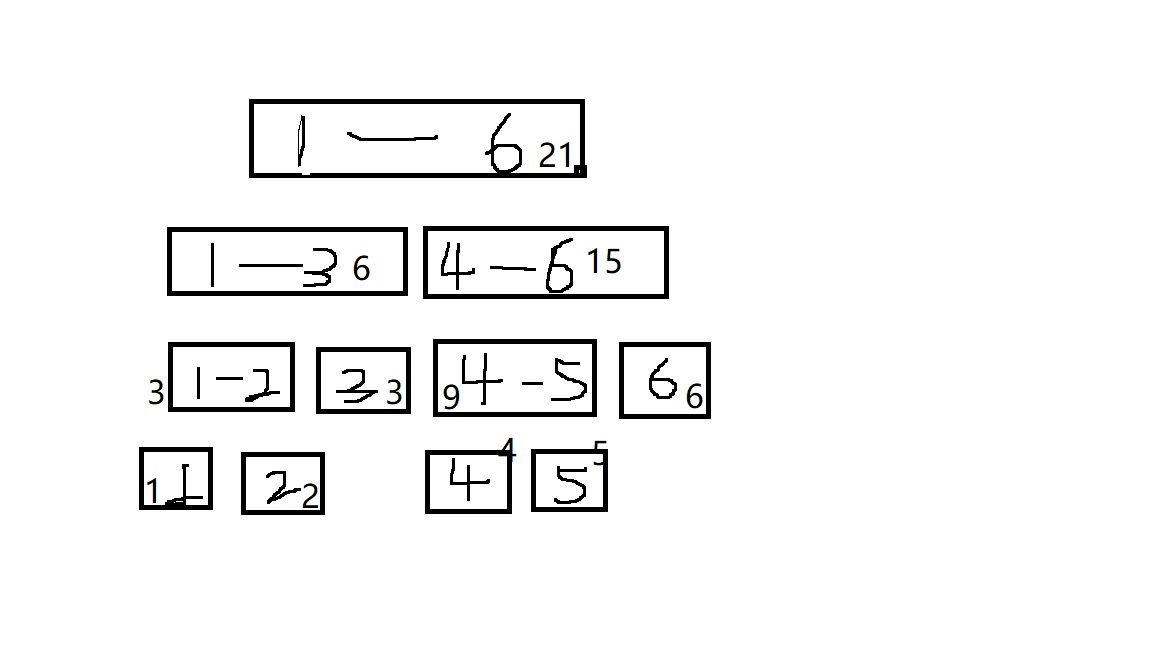
现在要把【3,5】区间上的每个数加1，

调用函数update(1,3,5,1,6,1)

L=3,R=5,l=1,r=6,val=1

mid = (1+6)<<1 = 3;

if(3<=3)满足，update(2,3,5,3,3,1)

L=3，R=5，l=r=3

if(3<=3&&3<=5)满足，更新数据和懒标记如图（紫色为兰标记，红色为更新的数值），return

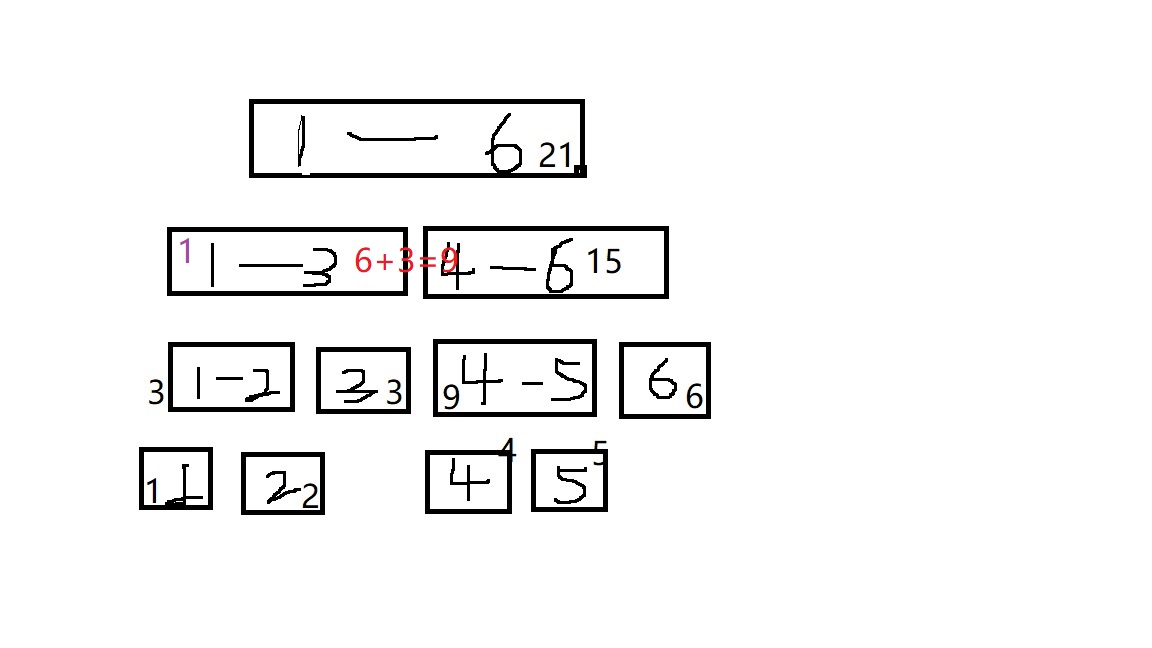
回到上一个update

if(3<5)满足，update(3,3,5,4,6,1)

L=3,R=5,l=4,r=6,val=1

这一个update下，mid=5

if(3<=5)满足，update(6,3,5,4,5,1)

if(3<=4&&5<=5)满足，更新数据和懒标记如图

 

在这一个update,

if(5<5)不满足，返回，

回溯过程中更新了数据域，如图（注意此时懒惰标记位置）

完成操作

查询【3,5】的区间和

类似于update的执行过程，最终得结果15

（6）参考文章：

，夜深人静写算法（七）- 线段树，https://blog.csdn.net/WhereIsHeroFrom/article/details/78969718

AC_King，线段树详解，https://www.cnblogs.com/AC-King/p/7789013.html

Dijkstra_Liu，线段树 从入门到进阶，https://www.cnblogs.com/jason2003/p/9676729.html

 

posted @ 2019-07-19 12:25  小张人  阅读(341)  评论(0)  编辑  收藏  举报
分享到：