1.2 - 概率论

1.2.1 概率认识

　　a）什么是概率：通俗的讲，概率就是 随机事件发生的可能性大小。

　　b）概率的公理化定义：设随机试验的样本空间Ω，若按照某种方法，对样本空间中的每一个事件 A 都赋予一个实数值 P(A)，且符合以下性质：

　　　　1）非负性：P(A) ≥ 0

　　　　2）规范性：P(Ω) = 1

　　　　3）(无限)可列可加性：对于两两互不相容的可列的无穷多个事件 A1，A2，...，A_n，有 P(A1 ∪ A2 ... ∪ An）= P(A1) + P(A2) + ... + P(An)。

　　　　则：称 P(A) 为事件 A 的概率。

　　在上述的公理化定义中，只是说按照某种方法，对每个事件A产生了一个映射，只要是映射的结果符合下面的三条性质，这就叫做概率。

　　c）在概率的公理化定义中，概率的数值上的精确大小是没有意义的，其只是在描述一种可能性。某种程度上，概率比较的相对意义更重于概率数值的绝对意义。同一个样本空间中，一个事件A发生的概率是 0.6，而另一个事件B发生的概率是 0.2，我们可以认为事件A发生的可能性要大于事件B，但是事件A的概率具体是 0.60 还是0..61，0.70 这并不是太重要。（同一个实验用不同的符合概率公理化定义的概率公式来计算概率，可能会出现这种情况。）

 

1.2.2 概率分类

　　条件概率

　　全概率公式

　　贝叶斯公式：已知某种现象结果，求结果对应某个原因的概率。即：如果 P(A | B) 难以计算，可以通过贝叶斯公式先求 P(B | A) 。

 

1.2.3 概率求解

　　1）频率。当实验结果次数趋向于正无穷的时候，某个事件发生的频率会趋向于一个稳定值，这个稳定的 似然值 可看作概率。（该方法实质也是一种最大似然估计，并且我们认为：之所以在无限次实验时频率会趋向稳定值，是因为这样可能性最大，即：这个稳定值为这个事件的概率。）

　　2）若符合古典概型 =》P = 1 / n 

　　3）利用概率的性质以及 全概率公式 + 贝叶斯。

　　4）其它 统计学&机器学习 方法。

 

1.2.4 机器学习方法求概率

　　在机器学习领域，经常需要预估一个事件发生概率的大小，并且通常难以用经典概率论方法求解。例如：空间中有两团点且两团点略有交集，这时候又来了一个新的点，这个点是落在两团中的哪一团？在机器学习中，我们可以在空间中设置一个超平面，这个超平面能够将这两团点分开在两侧。 当点与超平面的距离  -> +∞ 时，点归属于超平面上方一团的可能性就越大直到1，当点与超平面距离趋向于 -∞ 时，点归属于超平面下方一团的可能性就越小直到0。当点恰好坐在超平面上时，点的类别归属于两团的可能性相等。当点距平面的距离在变化的时候，点实际归属类别的可能性也在变化。  在这个案例中，每个来新的点都是一次随机实验，点落在超平面上方、下方和恰好落在超平面上是随机实验下的三个事件，所有的落点实验组成了样本空间。这种用距离数值映射概率的过程特性，完全符合概率的公理化定义。

　　这种将距离映射到概率的思路是可行的，但是概率的有效值区间：[0, 1]，如何找到一个合适的映射函数，将距离转换为概率值呢？

　　常用的映射函数：

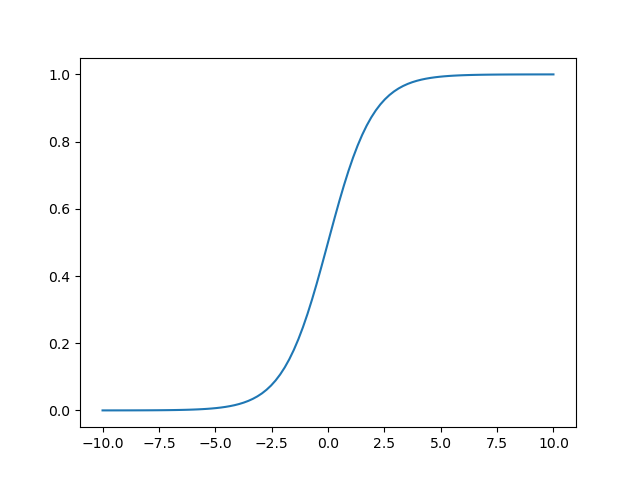
　　　　1）logistic（sigmoid）函数（二分类）：1/（1 + e^-x）

　　

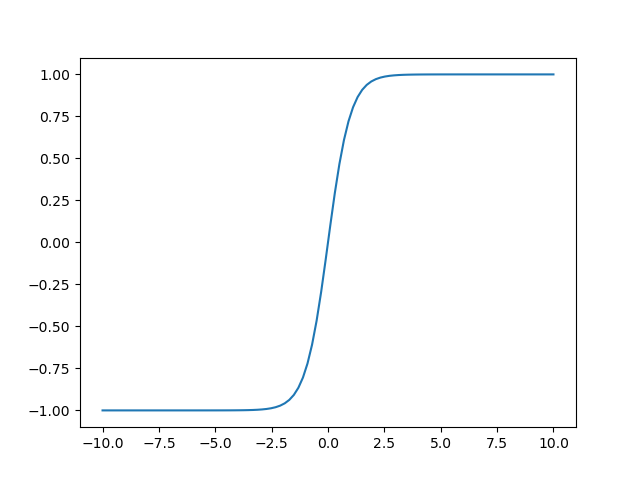
　　　　2）双曲正切函数 tanh(x)：（e^x - e^-x）/（e^x + e^-x）

　　

　　　　3）softmax函数（多分类，通常是 ≥3 维的向量）：S_i = eⁱ / ∑S_i 

 

小结，概率的意义：

　　概率大小只有相对意义，并不代表最终结果。前期98%，99%的胜率也可能会后期被对手翻盘，如 战鹰熬老太太。概率本身就是不确定性。所以，98%，99%在某些情况下并没有什么意义。但是在推荐商品的时候，我们肯定还是首推用户匹配度99%的商品而不是98%的。 概率本身的意义就是在促成一些东西，并不断的积累有利因素的一个过程，但是在最终结果出来之前，得到的概率值再大也不能代表最终一定会这样，这只阐述了一种可能性。在最终结果之前过程之中，我们能做的只是 尽可能的让我们想要的结果的发生的概率足够大，但是概率足够大就一定会发生吗？倒也未必，只是很可能会发生。