可持久化平衡树

可持久化平衡树

• 可持久化的数据结构，其核心都是不改变历史的信息。当需要对信息进行修改的时候就新开一个节点，继承历史信息，然后再进行修改。
• 带旋转的平衡树会改变祖先关系，这令可持久化变得困难。所以需要使用非旋的平衡树，如非旋treap。
• 和普通平衡树的区别其实有且仅有每次分裂和合并时不覆盖（直接使用）之前的节点，而是新建节点。因为这样才能保证历史信息一直存在，方便后面调用。

对于非旋treap来说，主要是对 Split/分裂 和 Merge/合并 两个操作进行可持久化。剩下的操作不会对数据产生影响。而考虑到非旋treap上的操作在 Split 后一定跟随着对应的 Merge ，所以不需要对每个 Split 和 Merge 操作都进行可持久化。只要实现 Insert 和 Delete 的可持久化即可。

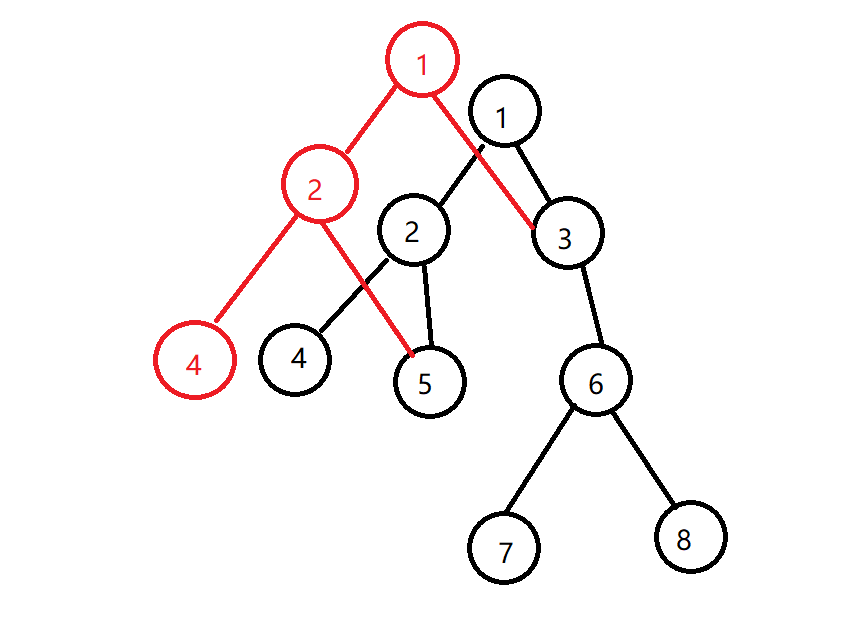
• 具体来讲，在 Split 过程中，我们分裂出来的两颗树不是在原树上进行操作，而是新建根然后分裂。此时会发现，分裂出来的两棵树与原树有很大的重合，所以我们借鉴线段树可持久化的操作，对这些节点进行复用即可。
• 也就是说，我们只要复制我们走过的每一个节点即可完成可持久化。对于 Merge 操作同理，新建节点然后合并即可。

如图

例题
洛谷 P3835 【模板】可持久化平衡树

代码

#include<bits/stdc++.h>
using namespace std;
int rt[500010];
struct jade
{
    int l,r,siz,v,key;
}t[500010*80];
int tot=0;
int init(int x)
{
    tot++;
	t[tot]={0,0,1,x,rand()};
	return tot;	
} 
void pushup(int ro)
{
    t[ro].siz=t[t[ro].l].siz+t[t[ro].r].siz+1;	
} 
void split(int ro,int v,int &x,int &y)
{
    if(!ro)
    {
    	x=y=0;
    	return ;
    }	
    if(t[ro].v<=v)
    {
        tot++;
		x=tot;
		t[x]=t[ro];
		split(t[x].r,v,t[x].r,y);
		pushup(x); 
	}
	else
	{
		tot++;
		y=tot;
		t[y]=t[ro];
		split(t[y].l,v,x,t[y].l);
		pushup(y);
	}
}
int merge(int x,int y)
{
	if(!x||!y)
	{
		return x+y;
	}
	tot++;
	int root=tot;
	if(t[x].key<t[y].key)
	{
		t[root]=t[x];
		t[root].r=merge(t[root].r,y);
	}
	else
	{
		t[root]=t[y];
		t[root].l=merge(x,t[root].l);
	}
	pushup(root);
	return root;
}
int kth(int ro,int k)
{
    if(t[t[ro].l].siz+1==k)
	{
	    return t[ro].v;	
	}	
	if(k<=t[t[ro].l].siz)
	{
		return kth(t[ro].l,k);
	}
	else
	{
		return kth(t[ro].r,k-t[t[ro].l].siz-1);
	}
} 
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int v,opt,k;
		cin>>v>>opt>>k;
		if(opt==1)
		{
			int x,y;
			split(rt[v],k,x,y);
			rt[i]=merge(merge(x,init(k)),y);
		}
		if(opt==2)
		{
			int x,y,z;
			split(rt[v],k,x,z);
			split(x,k-1,x,y);
			y=merge(t[y].l,t[y].r);
			rt[i]=merge(merge(x,y),z);
		}
		if(opt==3)
		{
			int x,y;
			split(rt[v],k-1,x,y);
			cout<<t[x].siz+1<<endl;
			rt[i]=merge(x,y);
		}
		if(opt==4)
		{
			cout<<kth(rt[v],k)<<endl;
			rt[i]=rt[v];
		}
		if(opt==5)
		{
		    int x,y;
			split(rt[v],k-1,x,y);
			if(!x)
			{
			    cout<<-2147483647<<endl; 
			}	
			else
			{
				cout<<kth(x,t[x].siz)<<endl;
			}
			rt[i]=merge(x,y);
		} 
		if(opt==6)
		{
			int x,y;
			split(rt[v],k,x,y);
			if(!y)
			{
				cout<<2147483647<<endl; 
			}
			else
			{
				cout<<kth(y,1)<<endl; 
			}
			rt[i]=merge(x,y);
		}
	}
    return 0;
} 

可持久化文艺平衡树

例题
洛谷 P5055【模板】可持久化文艺平衡树

难点在于懒标记的处理，如果直接下放可能会导致其他共用这个节点的树的信息改变，但是不下放的话这个标记并没有办法标记永久化。
考虑到可持久化的实质其实就是在每一次修改的时候复制节点进行操作，所以我们下放标记的时候复制一遍左右儿子然后再交换即可。

代码

#include<bits/stdc++.h>
using namespace std;
int rt[200010];
struct jade
{
    int l,r,siz,key,tag;
	long long v,sum;
}t[200010<<7];
int tot=0;
long long lastans;
int init(long long x=0)
{
    tot++;
	t[tot].v=x;
	t[tot].sum=x;
	t[tot].key=rand();
	t[tot].siz=1;
	return tot;	
} 
int copy(int ro)
{
	int x=init();
	t[x]=t[ro];
	return x;
}
void pushdown(int ro) 
{
	if(!t[ro].tag)
	{
		return;
	} 
	if(t[ro].l) 
	{
		t[ro].l=copy(t[ro].l);
		t[t[ro].l].tag^=1;
	}
	if(t[ro].r)
	{
		t[ro].r=copy(t[ro].r);
		t[t[ro].r].tag^=1;
	} 
	swap(t[ro].l,t[ro].r);
	t[ro].tag=0;
}
void pushup(int ro)
{
    t[ro].siz=t[t[ro].l].siz+t[t[ro].r].siz+1;
	t[ro].sum=t[t[ro].l].sum+t[t[ro].r].sum+t[ro].v;	
} 
void split(int ro,int v,int &x,int &y)
{
    if(!ro)
    {
    	x=y=0;
    	return ;
    }	
    pushdown(ro);
    if(t[t[ro].l].siz<v)
    {
		x=copy(ro);
		split(t[x].r,v-t[t[ro].l].siz-1,t[x].r,y);
		pushup(x); 
	}
	else
	{
	    y=copy(ro);
		split(t[y].l,v,x,t[y].l);
		pushup(y);
	}
}
int merge(int x,int y)
{
	if(!x||!y)
	{
		return x+y;
	}
	pushdown(x);
	pushdown(y);
	if(t[x].key<t[y].key)
	{
		t[x].r=merge(t[x].r,y);
		pushup(x);
		return x;
	}
	else
	{
		t[y].l=merge(x,t[y].l);
		pushup(y);
		return y;
	}
}
int main()
{
	int n;
	cin>>n;
	int x=0,y=0,z=0;
	for(int i=1;i<=n;i++)
	{
		int v,opt;
		cin>>v>>opt;
		if(opt==1)
		{
			long long a,b;
			cin>>a>>b;
			a^=lastans;
			b^=lastans;
			split(rt[v],a,x,y);
			rt[i]=merge(merge(x,init(b)),y);
		}
		if(opt==2)
		{
			long long a;
			cin>>a;
			a^=lastans;
			split(rt[v],a,x,z);
			split(x,a-1,x,y);
			rt[i]=merge(x,z);
		}
		if(opt==3)
		{
			long long a,b;
			cin>>a>>b;
			a^=lastans;
			b^=lastans;
			split(rt[v],b,x,z);
			split(x,a-1,x,y);
			t[y].tag^=1;
			rt[i]=merge(merge(x,y),z);
		}
		if(opt==4)
		{
			long long a,b;
			cin>>a>>b;
			a^=lastans;
			b^=lastans;
			split(rt[v],b,x,z);
			split(x,a-1,x,y);
			lastans=t[y].sum;
			cout<<t[y].sum<<endl;
			rt[i]=merge(merge(x,y),z);
		}
	}
    return 0;
} 

\({\scr {The }}\) \({\scr {end. }}\)